• 快排（霍尔排序实现+前后指针实现）（递归+非递归）

    前言

    快排是很重要的排序，也是一种比较难以理解的排序，这里我们会用递归的方式和非递归的方式来解决，递归来解决是比较简单的，非递归来解决是有点难度的

    快排也称之为霍尔排序，因为发明者是霍尔，本来是命名为霍尔排序的，但是霍尔这个人对于自己创造的排序很自信，所以命名为快排

    当然也是如他所料，快排确实很快，但是还没有达到第一批次那个程度

    快排gif

    快排实现逻辑排序

    单趟实现逻辑:
    1.假设左边为keyi，也就是对比数值
    2，右边R先走，循环寻找比keyi小的数值
    3，左边l走，循环寻找比keyi大的数值
    4，交换找到的比keyi大的数值和小的数值，此时会导致小的在左边，大的在右边，最后相遇的时候交换keyi和相遇的元素

    多趟实现:
    1，多趟实现可以采取递归和非递归，但是总体逻辑都是一样的，这里先讲解一下递归的方式2，此时，我们会发现keyi下标所在位置，就是从前往后6，的位置，所以6回到自己的位置，我们以keyi为分界点进行切割【left,keyi-1】keyi【keyi+1,right】
    进行递归，从而实现简易版的速排
    完善逻辑:
    1，此时是快排还是有点问题的，当数值本身就是顺序的时候
    会发现此时的时间复杂度就变成了n^2，也就是不快了
    2，原因是当本身就是排序好的时候，right右边会一直往左边寻
    找，直到找到left，和自己交换，此时的时间复杂度也就是
    n,n-1..1.0
    3，解决办法，我们可以三个数值取中，什么意思?也就是不管什么情况，我们都取出前三个数值，比如这里的
    6 1 2
    我们取出6 1 2，取出中间的位置，2，和keyi进行交换其他逻辑不变
    完善逻辑:
    1，此时我们发现逻辑没有问题，但是速度还是和堆排序有点差距，那么此时我们继续进行优化
    2，因为这里是用递归来实现的，我们发现，递归的实现是逐级实现的，也就是
    第-层->第n层:1->2->3->4->…->n-1->n
    这样的递归方式来实现的，所以越到下面，递归的越多
    我们可以把最后十层的递归用插入排序来实现一下，
    3，为什么用插入排序?在排序里面有希尔排序，冒泡排序，选
    择排序，堆排序
    希尔排序->插入排序的进阶(书写复杂)
    冒泡排序->时间复杂度高
    选择排序->时间复杂度和冒泡一样，比较高
    堆排序->处理大型数字问题，这里没必要
    所以我们采取插入排序的方式进行解决
    4，解决，我们只需要在递归的时候加一个判断，就可以，当数
    值小于等于10 的时候，我们直接调用插入排序解决问题。
    此时速排(霍尔排序)，递归的方式也就结束了。

    图解：

    快排单趟实现

    快排多趟实现

    简易版本的代码实现

    1. //霍尔方法(递归实现)
    2. void QuickSort01(int* a, int left, int right)
    3. {
    4. 	//递归停止条件
    5. 	if (left >= right)
    6. 		return;
    7. 	//单趟实现
    8. 	//右边找小，左边找大
    9. 	int begin = left; int end = right;
    10. 	int keyi = begin;
    11. 	while (begin < end)
    12. 	{
    13. 		//右边找小，不是的话移动,是的话不移动，并且跳出循环
    14. 		while (begin < end && a[keyi] <= a[end])
    15. 		{
    16. 			end--;
    17. 		}
    18. 		//左边找大，不是的话移动，是的话不移动，并且跳出循环
    19. 		while (begin < end && a[keyi] >= a[begin])
    20. 		{
    21. 			begin++;
    22. 		}
    23. 		Swap(&a[begin], &a[end]);
    24. 	}
    25. 	Swap(&a[keyi], &a[begin]);
    26. 	keyi = begin;
    27. 	//多趟递归实现
    28. 	//[left,keyi-1] keyi [keyi+1,right]   这里传递的是区间
    29. 	//  1     0      1     2      1       当只剩一个数值的时候，也就是这个区间的时候，递归停止 
    30. 	QuickSort01(a, left, keyi - 1);
    31. 	QuickSort01(a, keyi + 1, right);
    32. }

    解释：

    1. 函数定义：QuickSort01函数接受一个整数数组的指针a以及两个整数left和right，分别表示要排序的数组部分的起始和结束索引。

    2. 递归终止条件：如果left大于或等于right，则当前子数组无需排序，递归结束。

    3. 初始化：设置两个指针begin和end分别指向子数组的起始和结束位置，keyi作为基准元素的索引，初始位置设为left。

    4. 单趟排序：

      • 使用两个内层循环，一个从右侧向左寻找比基准值小的元素，另一个从左侧向右寻找比基准值大的元素。
      • 当找到合适的元素时，交换这两个元素的位置，然后继续寻找，直到begin和end相遇。

    5. 基准值定位：将基准值a[keyi]与begin指向的元素交换，此时begin指向的位置是基准值的最终位置。

    6. 递归排序：对基准值左边的子数组[left, keyi - 1]和右边的子数组[keyi + 1, right]递归调用QuickSort01函数进行排序。

    7. 效率：快速排序的平均时间复杂度为O(n log n)，但在最坏情况下（如数组已经排序）时间复杂度会退化到O(n^2)。霍尔方法通过减少不必要的数据交换来提高排序效率。

    8. 辅助函数：Swap函数用于交换两个元素的值，虽然在代码中未给出定义，但它是快速排序中交换元素的关键操作。

    快速排序算法的效率和性能在实际应用中通常优于其他O(n log n)算法，如归并排序，尤其是在数据量较大时。然而，其稳定性不如归并排序，且在最坏情况下性能较差。在实际应用中，快速排序通常与其他排序算法结合使用，以提高整体排序性能。

    注意事项

    注意事项1

    这里有一个关键点是很重要的，也就是我们是从右边先出发的，因为我们的keyi的位置在左边。

    如果我们的keyi的下标在左边，并且左边先走的话，就会产生一种结果

    如图

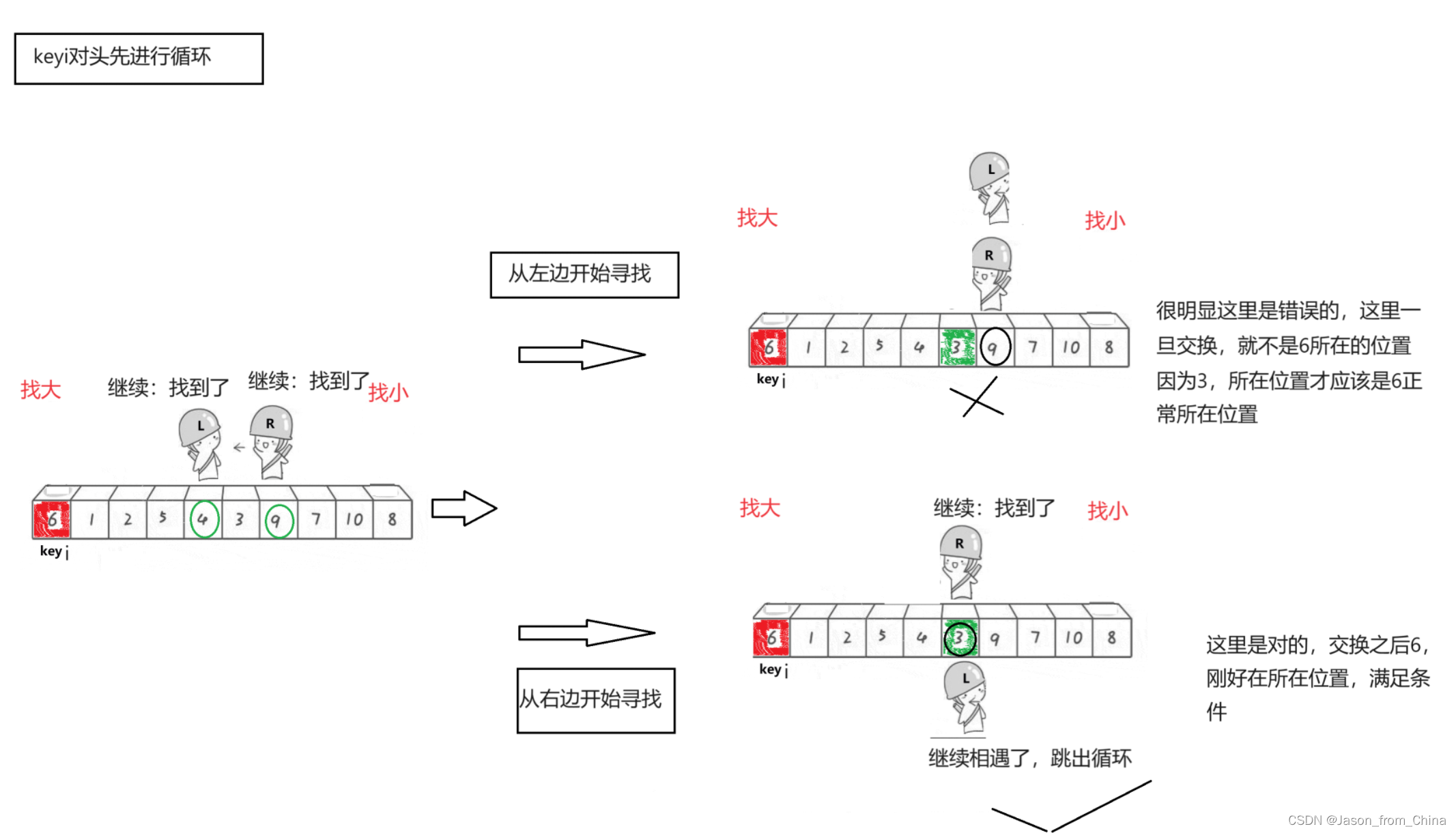
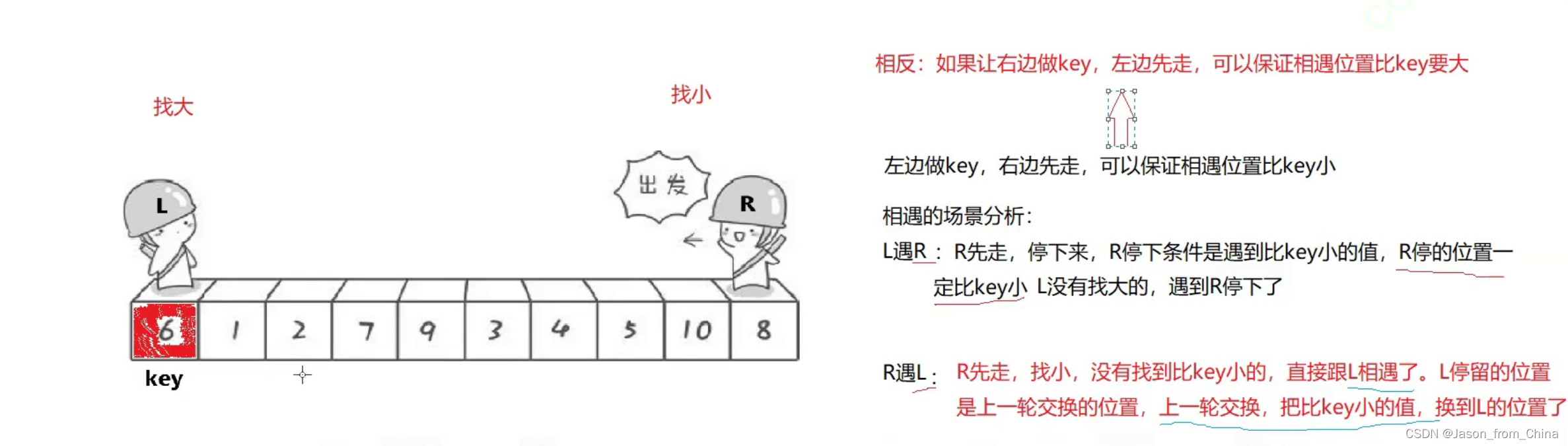
    注意事项2

    不是等于就交换，是等于会跳过往下找

    当我们写的是不等于的时候

    快排完整代码实现-（三数值取中）

    此时存在的最大问题就是如果排序本身就是顺序排序的情况下，这时间复杂度反而高了，所以我们对排序进行修改

    1. //交换函数
    2. void Swap(int* p1, int* p2)
    3. {
    4. 	int tmp = *p1;
    5. 	*p1 = *p2;
    6. 	*p2 = tmp;
    7. }
    8. //霍尔方法(递归实现)
    9. //三数取中
    10. int GetMid(int* a, int left, int right)
    11. {
    12. 	//三数取中传参的是下标，我们取中也是根据下标进行计算的
    13. 	int mid = (left + right) / 2;
    14. 	if (a[left] < a[right])
    15. 	{
    16. 		if (a[mid] < a[left])//a[mid] < a[left] < a[right]
    17. 		{
    18. 			return left;
    19. 		}
    20. 		else if(a[mid] > a[right])// a[left] < a[right] < a[mid] 
    21. 		{
    22. 			return right;
    23. 		}
    24. 		else
    25. 		{
    26. 			return mid;
    27. 		}
    28. 	}
    29. 	else//a[left] > a[right]
    30. 	{
    31. 		if (a[mid] > a[left])//a[mid] > a[left] > a[right]
    32. 		{
    33. 			return left;
    34. 		}
    35. 		else if (a[mid] < a[right])//a[left] > a[right] > a[mid] 
    36. 		{
    37. 			return right;
    38. 		}
    39. 		else
    40. 		{
    41. 			return mid;
    42. 		}
    43. 	}
    44. }
    45. void QuickSort01(int* a, int left, int right)
    46. {
    47. 	//递归停止条件
    48. 	if (left >= right)
    49. 		return;
    50. 	//三数取中
    51. 	int mid = GetMid(a, left, right);
    52. 	Swap(&a[mid], &a[left]);
    53. 	//单趟实现
    54. 	//右边找小，左边找大
    55. 	int begin = left; int end = right;
    56. 	int keyi = begin;
    57. 	while (begin < end)
    58. 	{
    59. 		//右边找小，不是的话移动,是的话不移动，并且跳出循环
    60. 		while (begin < end && a[keyi] <= a[end])
    61. 		{
    62. 			end--;
    63. 		}
    64. 		//左边找大，不是的话移动，是的话不移动，并且跳出循环
    65. 		while (begin < end && a[keyi] >= a[begin])
    66. 		{
    67. 			begin++;
    68. 		}
    69. 		Swap(&a[begin], &a[end]);
    70. 	}
    71. 	Swap(&a[keyi], &a[begin]);
    72. 	keyi = begin;
    73. 	//多趟递归实现
    74. 	//[left,keyi-1] keyi [keyi+1,right]   这里传递的是区间
    75. 	//  1     0      1     2      1       当只剩一个数值的时候，也就是这个区间的时候，递归停止 
    76. 	QuickSort01(a, left, keyi - 1);
    77. 	QuickSort01(a, keyi + 1, right);
    78. }

    总结：

    1. 函数目的：选择一个合适的基准值，以提高快速排序算法的效率。

    2. 传入参数：接受一个整数数组的指针a，以及表示数组部分边界的整数left和right。

    3. 计算中间索引：通过(left + right) / 2计算中间元素的索引mid。

    4. 三数取中逻辑：

      • 如果数组的第一个元素a[left]小于最后一个元素a[right]：
        • 如果中间元素a[mid]小于第一个元素，则选择第一个元素作为基准。
        • 如果中间元素大于最后一个元素，则选择最后一个元素作为基准。
        • 否则，选择中间元素作为基准。
      • 如果第一个元素大于或等于最后一个元素（即数组首尾元素已经排序或相等）：
        • 如果中间元素大于第一个元素，则选择第一个元素作为基准。
        • 如果中间元素小于最后一个元素，则选择最后一个元素作为基准。
        • 否则，选择中间元素作为基准。

    5. 返回值：函数返回基准值的索引。

    6. 优化目的：通过三数取中法选择基准，可以减少快速排序在特定情况下性能退化的问题，如数组已经排序或包含大量重复元素。

    7. 适用场景：适用于快速排序算法中，作为选择基准值的策略。

    8. 性能影响：选择一个好的基准值可以确保数组被均匀地划分，从而接近快速排序的最佳平均时间复杂度O(n log n)。

    三数取中法是一种简单而有效的基准选择策略，它通过比较数组的首元素、尾元素和中间元素，来确定一个相对平衡的基准值，有助于提高快速排序的整体性能和稳定性。

    快排完整代码实现-（减少递归次数）

    此时我们还面临的问题就是底层的递归次数过多的问题，递归会随着次数的增加呈现倍数增长，就像三角形一样

    最后我们减少递归次数，把最底层从递归改为插入排序，逻辑完成

    快排完整代码

    1. //交换函数
    2. void Swap(int* p1, int* p2)
    3. {
    4. 	int tmp = *p1;
    5. 	*p1 = *p2;
    6. 	*p2 = tmp;
    7. }
    8. //霍尔方法(递归实现)
    9. //三数取中
    10. int GetMid(int* a, int left, int right)
    11. {
    12. 	//三数取中传参的是下标，我们取中也是根据下标进行计算的
    13. 	int mid = (left + right) / 2;
    14. 	if (a[left] < a[right])
    15. 	{
    16. 		if (a[mid] < a[left])//a[mid] < a[left] < a[right]
    17. 		{
    18. 			return left;
    19. 		}
    20. 		else if(a[mid] > a[right])// a[left] < a[right] < a[mid] 
    21. 		{
    22. 			return right;
    23. 		}
    24. 		else
    25. 		{
    26. 			return mid;
    27. 		}
    28. 	}
    29. 	else//a[left] > a[right]
    30. 	{
    31. 		if (a[mid] > a[left])//a[mid] > a[left] > a[right]
    32. 		{
    33. 			return left;
    34. 		}
    35. 		else if (a[mid] < a[right])//a[left] > a[right] > a[mid] 
    36. 		{
    37. 			return right;
    38. 		}
    39. 		else
    40. 		{
    41. 			return mid;
    42. 		}
    43. 	}
    44. }
    45. void QuickSort01(int* a, int left, int right)
    46. {
    47. 	//递归停止条件
    48. 	if (left >= right)
    49. 		return;
    50. 	//当区间数值小于10个，此时我们直接采取插入排序进行排序
    51. 	if (right - left + 1 <= 10)
    52. 	{
    53. 		//这里记得是左右区间，所以不能只传递a，而是传递a + left
    54. 		InsertionSort(a + left, right - left + 1);
    55. 	}
    56. 	else
    57. 	{
    58. 		//三数取中
    59. 		int mid = GetMid(a, left, right);
    60. 		Swap(&a[mid], &a[left]);
    61. 		//单趟实现
    62. 		//右边找小，左边找大
    63. 		int begin = left; int end = right;
    64. 		int keyi = begin;
    65. 		while (begin < end)
    66. 		{
    67. 			//右边找小，不是的话移动,是的话不移动，并且跳出循环
    68. 			while (begin < end && a[keyi] <= a[end])
    69. 			{
    70. 				end--;
    71. 			}
    72. 			//左边找大，不是的话移动，是的话不移动，并且跳出循环
    73. 			while (begin < end && a[keyi] >= a[begin])
    74. 			{
    75. 				begin++;
    76. 			}
    77. 			Swap(&a[begin], &a[end]);
    78. 		}
    79. 		Swap(&a[keyi], &a[begin]);
    80. 		keyi = begin;
    81. 		//多趟递归实现
    82. 		//[left,keyi-1] keyi [keyi+1,right]   这里传递的是区间
    83. 		//  1     0      1     2      1       当只剩一个数值的时候，也就是这个区间的时候，递归停止 
    84. 		QuickSort01(a, left, keyi - 1);
    85. 		QuickSort01(a, keyi + 1, right);
    86. 	}
    87. }

    代码解释：

    1. 三数取中函数 GetMid:

      • 计算中间索引 mid。
      • 通过比较数组的首元素、尾元素和中间元素，选择一个合适的基准值。
      • 如果首元素小于尾元素，选择中间元素和首尾元素中较小或较大的一个作为基准。
      • 如果首元素大于尾元素，选择中间元素和首尾元素中较大或较小的一个作为基准。

    2. 快速排序函数 QuickSort01:

      • 递归停止条件：如果当前区间的左右索引 left 和 right 交叉或重合，则不需要排序。
      • 当区间大小小于或等于10时，使用插入排序，因为小数组上插入排序更高效。
      • 使用 GetMid 函数获取基准值的索引，并将基准值与首元素交换。
      • 霍尔方法的分区操作，通过两个指针 begin 和 end 进行分区。
      • 递归地对基准值左边和右边的子区间进行快速排序。

    3. 辅助函数 Swap:

      • 交换两个元素的值，虽然代码中未给出定义，但通常是一个简单的值交换操作。

    总结：

    • 算法优化: 通过三数取中法选择基准值，可以提高基准值的选中质量，从而提高快速排序的效率。
    • 小数组优化: 当子数组的大小，小于或等于10时，使用插入排序代替快速排序，因为小数组上插入排序的性能通常更好。
    • 递归与迭代: 快速排序是一个递归算法，但在小数组上切换到迭代的插入排序可以减少递归开销。
    • 分区策略: 使用霍尔方法进行分区，这是一种高效的分区策略，可以减少不必要的数据交换。
    • 适用场景: 这种改进的快速排序适用于大多数需要排序的场景，尤其是在大数据集上，它能够保持较好的性能。
    • 时间复杂度: 平均情况下时间复杂度为 O(n log n)，最坏情况下（已排序数组）时间复杂度为 O(n^2)，但由于三数取中法和插入排序的结合，最坏情况出现的概率降低。

    通过这种改进，快速排序算法在处理小数组时更加高效，同时在大数据集上也能保持较好的性能，使其成为一种更加健壮的排序算法。

    快排的时间复杂度

    快速排序算法的时间复杂度取决于分区过程中基准值的选择。

    理想情况下

    基准值会将数组均匀地分成两部分，每部分的元素数量大致相等。对于这种理想情况，快速排序的时间复杂度是 O(n log n)，其中 n 是数组中的元素数量。

    最坏情况下

    如果基准值的选择非常不均匀，从而导致每次分区都极不平衡，快速排序的最坏时间复杂度会退化到 O(n^2)。这种情况通常发生在数组已经排序或所有元素相等的情况下。

    在当前代码中

    使用了三数取中法来选择基准值，这种方法可以在大多数情况下避免选择极端值作为基准，从而减少最坏情况发生的概率。但是，如果数组的元素分布非常不均匀，或者存在大量重复元素，仍然可能遇到性能退化的情况。

    此外，代码中还引入了一个优化：当子数组的大小小于或等于10时，使用插入排序而不是快速排序。这是因为对于小数组，插入排序的性能通常比快速排序更好，而且插入排序是稳定的。这个优化可以提高算法在处理小数组时的效率。

    总的来说，这个改进的快速排序算法的平均时间复杂度是 O(n log n)，但在最坏情况下仍然是 O(n^2)。然而，由于三数取中法和插入排序的优化，最坏情况的发生概率被大大降低了。在实际应用中，这种改进的快速排序算法通常能够提供非常高效的排序性能。

    前后修改之后速度进行对比

    优化，和不优化之间的区别

    这里计算的是一千万个数值进行排序的毫秒数值，也就是不到一秒，还是很快的，尤其是修改之后，解决了大量的递归问题

    注意事项

    这里调用的插入排序是升序，写的快排也是升序，如果你需要测试降序，那么你需要把插入排序一起改成降序，不然会导致排序冲突

    快排（前后指针-递归解决）

    前言

    快排解决办法有很多种，这里我再拿出来一种前后指针版本

    虽然这个版本的时间复杂度和霍尔一样，逻辑也差不多，但是实际排序过程，确实会比霍尔慢一点

    快排gif

    快排前后指针实现逻辑：

    前后指针实现逻辑(升序):
    单趟排序:
    1，我们使用递归来进行实现，所以我们先实现单趟排序
    2，定义两个下标，也就是所谓的指针，初始的时候，一个指向最左边第一个元素(prev)，一个指向第二个元素(cur)，最后定义一个对比keyi3，此时先判断我们的cur是不是小于keyi。cur小于keyi的话:prev++，交换，之后cur++4，但是我们如果和自己交换此时没有什么意义，所以这里我们需要做一个处理
    5，继续往前走，如果遇见的是:比keyi下标大的元素此时，cur++，直到遇见的是比keyi下标小的元素，循环执行.prev++，交换，之后cur++

    6，最后cur走到最后一个元素，我们交换keyi的下标元素和prev的下标元素

    多趟实现:
    1，递归进行分割:【left，keyi-1】keyi【keyi+1，right】
    2，停止条件就是当left>=right
    原因:【left, keyi-1】keyi【keyi+1, right】

    快排单趟实现

    这里只是图解单趟实现逻辑，因为多趟实现的逻辑和霍尔的一样，也是递归，所以不进行多次书写

    代码实现

    这里的代码实现的核心逻辑不一样，大的框架是一样的，也就是三数取中，以及减少递归从而使用插入排序这样的逻辑是一样的，下面我们来看看这个新的组装怪

    1. //快排（前后指针方法）(递归实现)
    2. void QuickSort02(int* a, int left, int right)
    3. {
    4. 	//递归停止条件
    5. 	if (left >= right)
    6. 		return;
    7. 	//创建两个变量，作为前后指针使用
    8. 	int prev = left; int cur = prev + 1;
    9. 	int keyi = left;
    10. 	//当快指针到尾的时候，跳出循环->交换
    11. 	while (cur <= right)
    12. 	{
    13. 		//前后指针中间是比a[keyi]大的数值，所以遇见大的++，小的停止
    14. 		if (a[keyi] > a[cur])
    15. 		{
    16. 			//停止之后，慢指针++,并且进行交换,因为中间才是大的数值，cur遇见大数值++。遇见小数值才停下来
    17. 			prev++;
    18. 			Swap(&a[prev], &a[cur]);
    19. 			//同理快指针也进行++，往后移动
    20. 			cur++;
    21. 		}
    22. 		else
    23. 		{
    24. 			cur++;
    25. 		}
    26. 	}
    27. 	Swap(&a[prev], &a[keyi]);
    28. 	keyi = prev;
    29. 	//多趟递归实现
    30. 	//[left,keyi-1] keyi [keyi+1,right]   这里传递的是区间
    31. 	//  1     0      1     2      1       当只剩一个数值的时候，也就是这个区间的时候，递归停止 
    32. 	QuickSort02(a, left, keyi - 1);
    33. 	QuickSort02(a, keyi + 1, right);
    34. }

    总结：

    1. 算法基础：快速排序是一种分而治之的排序算法，它通过递归地将数组分为较小的子数组，然后对这些子数组进行排序。

    2. 分区策略：使用前后指针（prev和cur）进行分区，而不是传统的左右指针。这种方法在某些情况下可以减少元素交换的次数。

    3. 基准值选择：基准值（keyi）是数组的第一个元素，即left索引对应的元素。

    4. 指针移动规则：

      • prev作为慢指针，用于跟踪比基准值小的元素的边界。
      • cur作为快指针，从left + 1开始遍历数组。

    5. 元素交换：当快指针指向的元素大于基准值时，不进行交换，快指针继续移动；当快指针指向的元素小于或等于基准值时，与慢指针所指元素交换，然后慢指针和快指针都向前移动。

    6. 递归排序：在基准值确定之后，递归地对基准值左边和右边的子数组进行排序。

    7. 时间复杂度：平均情况下，快速排序的时间复杂度为O(n log n)。最坏情况下，如果每次分区都极不平衡，时间复杂度会退化到O(n^2)。

    8. 空间复杂度：由于递归性质，快速排序的空间复杂度为O(log n)。

    9. 算法优化：通过前后指针方法，可以在某些情况下提高快速排序的性能，特别是当基准值接近数组中间值时。

    10. 适用场景：快速排序适用于大多数需要排序的场景，特别是在大数据集上，它通常能够提供非常高效的排序性能。

    优化

    这里我们可以看到，cur无论是if还是else里面都需要++，所以我们直接放到外面

    其次我们为了效率，不和自己交换，我们不和自己交换，进行一个判断条件

    快慢指针代码优化（完整）

    1. //交换函数
    2. void Swap(int* p1, int* p2)
    3. {
    4. 	int tmp = *p1;
    5. 	*p1 = *p2;
    6. 	*p2 = tmp;
    7. }
    8. //快排（前后指针方法）(递归实现)
    9. void QuickSort02(int* a, int left, int right)
    10. {
    11. 	//递归停止条件
    12. 	if (left >= right)
    13. 		return;
    14. 	if (right - left + 1 >= 10)
    15. 	{
    16. 		InsertionSort(a + left, right - left + 1);
    17. 	}
    18. 	else
    19. 	{
    20. 		//三数取中
    21. 		int mid = GetMid(a, left, right);
    22. 		Swap(&a[mid], &a[left]);
    23.  
    24. 		//单趟实现
    25. 		//创建两个变量，作为前后指针使用
    26. 		int prev = left; int cur = prev + 1;
    27. 		int keyi = left;
    28. 		//当快指针到尾的时候，跳出循环->交换
    29. 		while (cur <= right)
    30. 		{
    31. 			//前后指针中间是比a[keyi]大的数值，所以遇见大的++，小的停止
    32. 			if (a[keyi] > a[cur] && prev++ != cur)
    33. 			{
    34. 				//停止之后，慢指针++,并且进行交换,因为中间才是大的数值，cur遇见大数值++。遇见小数值才停下来
    35. 				Swap(&a[prev], &a[cur]);
    36. 			}
    37. 			cur++;
    38. 		}
    39. 		Swap(&a[prev], &a[keyi]);
    40. 		keyi = prev;
    41. 		//多趟递归实现
    42. 		//[left,keyi-1] keyi [keyi+1,right]   这里传递的是区间
    43. 		//  1     0      1     2      1       当只剩一个数值的时候，也就是这个区间的时候，递归停止 
    44. 		QuickSort02(a, left, keyi - 1);
    45. 		QuickSort02(a, keyi + 1, right);
    46. 	}
    47. }

    总结：

    1. 基本递归结构：算法使用递归调用来处理子数组，这是快速排序算法的核心结构。

    2. 小数组优化：当子数组的大小小于或等于10时，算法使用插入排序而不是快速排序，因为插入排序在小规模数据上更高效。

    3. 三数取中法：为了更均匀地分割数组，算法使用三数取中法选择基准值，这有助于减少最坏情况发生的概率。

    4. 前后指针方法：算法使用两个指针（prev和cur），其中prev作为慢指针，cur作为快指针，通过这种方式进行一次遍历完成分区。

    5. 分区操作：快指针从left + 1开始遍历，如果当前元素小于基准值，则与慢指针所指的元素交换，然后慢指针向前移动。

    6. 递归排序子数组：基准值确定后，算法递归地对基准值左边和右边的子数组进行排序。

    7. 时间复杂度：平均情况下，算法的时间复杂度为O(n log n)，最坏情况下为O(n^2)。但由于采用了小数组优化和三数取中法，最坏情况的发生概率降低。

    8. 空间复杂度：算法的空间复杂度为O(log n)，这主要由于递归调用导致的栈空间使用。

    9. 适用场景：这种改进的快速排序算法适用于大多数需要排序的场景，尤其是在大数据集上，它能够提供非常高效的排序性能，同时在小数据集上也表现出较好的效率。

    10. 算法稳定性：由于使用了插入排序对小规模子数组进行排序，算法在处理小规模数据时具有稳定性。

    11. 注意：在实际测试·里面，前后指针比霍尔排序慢一点

    通过这种混合排序策略，算法在保持快速排序优点的同时，也提高了在特定情况下的排序效率，使其成为一种更加健壮的排序方法。

    注意事项

    这里调用的插入排序是升序，写的快排也是升序，如果你需要测试降序，那么你需要把插入排序一起改成降序，不然会导致排序冲突

    快排（霍尔版本-非递归解决）

    前言

    快拍不仅需要学习递归，还需要学东西非递归，这样更有助于我们理解快拍

    首先我们需要知道，非递归的学习需要使用栈，所以如果我们的栈的学习是不完善的，建议学习一下栈

    非递归gif

    这里其实单词循环是谁其实不重要，可以是前后指针，也可以是霍尔方式，这里我们拿出来霍尔的gif来观看

    实现图解

    非递归实现主要是依赖栈来进行实现，依赖栈的特点，先进后出，后进前出

    1，首先我们需要写一个栈的库进行调用

    2，入区间，调用单次排序的实现思路

    3，入区间的时候，我们需要把握入栈和出栈的关键

    代码实现（前后指针）

    首先我们调用栈

    头文件

    1. #define _CRT_SECURE_NO_WARNINGS 1
    2. #pragma once
    3. #include
    4. #include
    5. #include
    6. typedef int STDataType;
    7. typedef struct Stack
    8. {
    9. 	STDataType* _a; // 首元素的地址
    10. 	int _top;		// 栈顶，初始化为0，也就是等同于size，初始化为-1，等同于下标
    11. 	int _capacity;  // 容量 
    12. }Stack;
    13. // 初始化栈 
    14. void StackInit(Stack* ps);
    15. // 销毁栈 
    16. void StackDestroy(Stack* ps);
    17. // 入栈 
    18. void StackPush(Stack* ps, STDataType data);
    19. // 出栈 
    20. void StackPop(Stack* ps);
    21. // 获取栈顶元素 
    22. STDataType StackTop(Stack* ps);
    23. // 获取栈尾元素 
    24. STDataType Stackhop(Stack* ps);
    25. // 获取栈中有效元素个数 
    26. int StackSize(Stack* ps);
    27. // 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
    28. int StackEmpty(Stack* ps);

    实现文件

    1. #include"Stack.h"
    2. // 初始化栈 
    3. void StackInit(Stack* ps)
    4. {
    5. 	ps->_a = NULL;
    6. 	ps->_capacity = ps->_top = 0;
    7. }
    8. // 销毁栈 
    9. void StackDestroy(Stack* ps)
    10. {
    11. 	assert(ps && ps->_top);
    12. 	free(ps->_a);
    13. 	ps->_a = NULL;
    14. 	ps->_capacity = ps->_top = 0;
    15. }
    16.  
    17. // 入栈 
    18. void StackPush(Stack* ps, STDataType data)
    19. {
    20. 	//判断需不需要扩容,相等的时候需要扩容
    21. 	if (ps->_capacity == ps->_top)
    22. 	{
    23. 		//判断空间是不是0，因为为0的时候，再多的数值*2,也是0
    24. 		int newcapacity = ps->_capacity == 0 ? 4 : ps->_capacity * 2;
    25. 		STDataType* tmp = (STDataType*)realloc(ps->_a, sizeof(STDataType) * newcapacity);
    26. 		if (tmp == NULL)
    27. 		{
    28. 			perror("StackPush:tmp:err:");
    29. 			return;
    30. 		}
    31. 		ps->_capacity = newcapacity;
    32. 		ps->_a = tmp;
    33. 	}
    34. 	ps->_a[ps->_top] = data;
    35. 	ps->_top++;
    36. }
    37.  
    38. // 出栈 
    39. void StackPop(Stack* ps)
    40. {
    41. 	assert(ps);
    42. 	ps->_top--;
    43. }
    44. // 获取栈顶元素 
    45. STDataType StackTop(Stack* ps)
    46. {
    47. 	//这里必须大于0 因为我们这里等同size，也就是个数，等于0都不行
    48. 	assert(ps);
    49. 	return ps->_a[ps->_top - 1];
    50. }
    51. // 获取栈尾元素 
    52. STDataType Stackhop(Stack* ps)
    53. {
    54. 	assert(ps && ps->_top > 0);
    55. 	return ps->_a[0];
    56. }
    57. // 获取栈中有效元素个数 
    58. int StackSize(Stack* ps)
    59. {
    60. 	//获取有效元素的时候，里面可以没有元素
    61. 	assert(ps);
    62. 	return ps->_top;
    63. }
    64. // 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
    65. int StackEmpty(Stack* ps)
    66. {
    67. 	//这里的判断是不是空，也就是里面是不是有数值，这里等于是一个判断，没有的话返回ture，有的话返回false
    68. 	assert(ps);
    69. 	return ps->_top == 0;
    70. }

    其次调用前后指针来实现

    1. //快排（前后指针方法）(单趟)
    2. int one_QuickSort02(int* a, int left, int right)
    3. {
    4. 	//三数取中
    5. 	//int mid = GetMid(a, left, right);
    6. 	//Swap(&a[mid], &a[left]);
    7.  
    8. 	//单趟实现
    9. 	//创建两个变量，作为前后指针使用
    10. 	int prev = left; int cur = prev + 1;
    11. 	int keyi = left;
    12. 	//当快指针到尾的时候，跳出循环->交换
    13. 	while (cur <= right)
    14. 	{
    15. 		//前后指针中间是比a[keyi]大的数值，所以遇见大的++，小的停止
    16. 		if (a[keyi] > a[cur] && prev++ != cur)
    17. 		{
    18. 			//停止之后，慢指针++,并且进行交换,因为中间才是大的数值，cur遇见大数值++。遇见小数值才停下来
    19. 			Swap(&a[prev], &a[cur]);
    20. 		}
    21. 		cur++;
    22. 	}
    23. 	Swap(&a[keyi], &a[prev]);
    24. 	return prev;                                                                                                                                                                   //快排 非递归实现
    25. void QuickSort003(int* a, int left, int right)
    26. {
    27. 	//非递归实现主要是用栈来模拟实现，在c++里面我们可以直接调用栈，但是在C语言里面我们只能写出来栈再进行调用
    28. 	//思路（霍尔方式）
    29. 	//1单趟的思路还是一样的，如果是升序的情况下，依旧是先从右边出发（找小），后从左边出发（找大）
    30. 	//2,循环递归过程我们改为利用进栈出栈来实现
    31. 	。首先我们需要明确这里传递的是区间，也就是利用栈实现的时候，我们传递的是数组和区间，利用区间进行计算
    32. 	。这里的关键在于传递区间的时候，我们需要详细知晓栈的特点，先进后出，后进后出，
    33. 	。所以在传递区间的时候，如果多趟循环，一分为二的时候，我们需要先传递右侧的区间，再传递左侧区间，因为我们需要先计算左侧
    34. 	。同理进去之后，我们需要继续入栈，需要先-入计算左侧的区间的右侧区间，后入左侧区间。这样就会先计算左侧区间
    35. 	。栈的特性，先进后出，后进先出
    36. 	// 
    37. 	// 所以这里我们把霍尔排序单趟实现来单独拿出来，这样的话我们接受的返回值是中间值
    38. 	//[left,keyi-1] keyi [keyi+1,right]
    39. 	//这里需要用非递归来解决
    40. 	Stack ps;
    41. 	StackInit(&ps);
    42. 	StackPush(&ps, right);
    43. 	StackPush(&ps, left);
    44. 	
    45. 	while (!StackEmpty(&ps))
    46. 	{
    47. 		int begin = StackTop(&ps);
    48. 		StackPop(&ps);
    49. 		int end = StackTop(&ps);
    50. 		StackPop(&ps);
    51.  
    52.         //假设入栈区间此时来到-> 0-2
    53. 		int mini = one_QuickSort02(a, begin, end);
    54. 		//经过计算之后，此时中间值是，keyi=1
    55. 		//0 1 2  三个区间三个数值，此时进行入栈判断
    56. 		//[begin,keyi-1]keyi[keyi+1,end]
    57. 		//[  0  ,  0   ] 1  [  2   , 2 ]
    58. 		//所以不继续入栈
    59.  
    60. 		if (mini + 1 < end)
    61. 		{
    62. 			//右边先入栈，后计算
    63. 			StackPush(&ps, end);
    64. 			StackPush(&ps, mini + 1);
    65. 		}
    66. 		if (mini - 1 > begin)
    67. 		{
    68. 			//左边区间后入栈，先计算
    69. 			StackPush(&ps, mini - 1);
    70. 			StackPush(&ps, begin);
    71. 		}
    72. 	}
    73.  
    74. 	StackDestroy(&ps);
    75. }

    解释：

    one_QuickSort02 函数

    这个函数是快速排序算法中的单趟排序实现。它使用前后指针法来实现，具体步骤如下：

    1. 初始化指针：prev 初始化为 left，cur 初始化为 prev + 1，keyi 也初始化为 left。
    2. 循环：当 cur 小于等于 right 时，执行循环体内的操作。
    3. 比较和交换：如果当前 cur 指向的元素小于 keyi 指向的元素，并且 prev 指针不等于 cur，说明找到了一个比基准值小的元素，需要交换。将 a[prev] 和 a[cur] 交换，并将 prev 指针向前移动一位。
    4. 移动快指针：无论是否发生交换，cur 指针都向前移动一位。
    5. 交换基准值：循环结束后，将 keyi 指向的元素与 prev 指向的元素交换，此时 prev 指向的是比基准值小的元素的最后一个位置。
    6. 返回值：函数返回 prev 的值，这个值是下一次分区的起始位置。

    QuickSort003 函数

    这个函数是快速排序的非递归实现，使用栈来模拟递归过程。具体步骤如下：

    1. 初始化栈：创建并初始化一个栈 ps。
    2. 入栈：将 left 和 right 作为初始区间入栈。
    3. 循环：只要栈不为空，就执行循环。
    4. 单趟排序：每次从栈中取出两个值作为区间的左右边界，调用 one_QuickSort02 函数进行单趟排序，得到中间值 mini。
    5. 判断区间：根据 mini 的位置，判断是否需要继续对左右区间进行排序。
      • 如果 mini + 1 < end，则说明右侧还有元素需要排序，将 end 和 mini + 1 入栈。
      • 如果 mini - 1 > begin，则说明左侧还有元素需要排序，将 begin 和 mini - 1 入栈。
    6. 出栈：每次循环结束，都会从栈中弹出两个值，直到栈为空。
    7. 销毁栈：循环结束后，销毁栈。

    对于栈和队列不是很明白的，推荐看一下栈和队列篇章

    数据结构-栈和队列(速通版本)-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/Jason_from_China/article/details/138715165

    代码实现（霍尔排序）

    这里其实不管是前后指针，还是霍尔排序，其实都是一样的，因为本质上都是让数值到应该到的位置，所以本质上是一样的，这里我再调用一个霍尔的方式是因为一方面和前后指针的调用形成对比，一方面有不同的注释

    1. //交换函数
    2. void Swap(int* p1, int* p2)
    3. {
    4. 	int tmp = *p1;
    5. 	*p1 = *p2;
    6. 	*p2 = tmp;
    7. }
    8. //霍尔方法(单趟实现)
    9. int one_QuickSort01(int* a, int left, int right)
    10. {
    11. 	//三数取中
    12. 	int mid = GetMid(a, left, right);
    13. 	Swap(&a[mid], &a[left]);
    14. 	//单趟实现
    15. 	//右边找小，左边找大
    16. 	int begin = left; int end = right;
    17. 	int keyi = begin;
    18. 	while (begin < end)
    19. 	{
    20. 		//右边找小，不是的话移动,是的话不移动，并且跳出循环
    21. 		while (begin < end && a[keyi] <= a[end])
    22. 		{
    23. 			end--;
    24. 		}
    25. 		//左边找大，不是的话移动，是的话不移动，并且跳出循环
    26. 		while (begin < end && a[keyi] >= a[begin])
    27. 		{
    28. 			begin++;
    29. 		}
    30. 		Swap(&a[begin], &a[end]);
    31. 	}
    32. 	Swap(&a[keyi], &a[begin]);
    33. 	return begin;
    34. }
    35. //霍尔方法再次调用
    36. void QuickSort03(int* a, int left, int right)
    37. {
    38. 	Stack ps;
    39. 	StackInit(&ps);
    40. 	StackPush(&ps, right);
    41. 	StackPush(&ps, left);
    42. 	while (!StackEmpty(&ps))
    43. 	{
    44. 		//取出左区间
    45. 		int begin = StackTop(&ps);
    46. 		StackPop(&ps);
    47. 		//取出右边区间
    48. 		int end = StackTop(&ps);
    49. 		StackPop(&ps);
    50.  
    51. 		int mini = one_QuickSort01(a, begin, end);
    52.  
    53. 		//计算区间
    54. 		//假设传递的区间是2-4 --->>> 传递过来的数值也就是下标是（1）4-2=2/2=1 --->>>此时mini=2,也就是此时我们返回的数值要么是第一个数值，要么的第二个数值的下标，不管是哪个，此时都会变成一个数值
    55. 		//此时我们继续入栈，入栈的是mini+1 也就是3-4，继续传递区间，此时传递回来的mini还是3，但是此时3+4==4了 所以不继续入栈，因为数值只有一个，不是区间了
    56. 		//右区间入栈，后出
    57. 		if (mini + 1 < end)
    58. 		{
    59. 			//入右边，之后左边，这样取的时候栈顶先取左边，之后右边
    60. 			StackPush(&ps, end);
    61. 			StackPush(&ps, mini + 1);
    62. 		}
    63. 		//左区间入栈，先出
    64. 		if (mini - 1 > begin)
    65. 		{
    66. 			StackPush(&ps, mini - 1);
    67. 			StackPush(&ps, begin);
    68. 		}
    69. 	}
    70. 	StackDestroy(&ps);
    71. }

    解释：

    one_QuickSort01 函数

    这个函数是霍尔快速排序算法的单趟实现，具体步骤如下：

    1. 三数取中：使用 GetMid 函数找到数组 a 中间位置的元素，并将其与数组第一个元素交换（left 索引位置的元素）。
    2. 初始化指针：begin 初始化为 left，end 初始化为 right，keyi 初始化为 begin。
    3. 循环：使用 while 循环，只要 begin 小于 end，就继续执行循环。
    4. 右边找小：从 end 向 begin 扫描，找到第一个小于基准值 a[keyi] 的元素。如果找到，end 指针向前移动，否则跳出循环。
    5. 左边找大：从 begin 向 end 扫描，找到第一个大于基准值 a[keyi] 的元素。如果找到，begin 指针向后移动，否则跳出循环。
    6. 交换元素：将找到的两个元素 a[begin] 和 a[end] 交换位置。
    7. 基准值交换：循环结束后，将 keyi 指向的元素与 begin 指向的元素交换，此时 begin 指向的是基准值的正确位置。
    8. 返回值：函数返回 begin 的值，这个值是下一次分区的起始位置。

    QuickSort03 函数

    这个函数是快速排序的非递归实现，使用栈来模拟递归过程：

    1. 初始化栈：创建并初始化一个栈 ps。
    2. 入栈：将初始区间的左右边界 left 和 right 入栈。
    3. 循环：只要栈不为空，就继续执行循环。
    4. 单趟排序：每次从栈中取出两个值作为区间的左右边界，调用 one_QuickSort01 函数进行单趟排序，得到中间值 mini。
    5. 计算新区间：根据 mini 的位置，计算新的左右区间。
      • 如果 mini + 1 < end，则说明右侧还有元素需要排序，将 end 和 mini + 1 入栈。
      • 如果 mini - 1 > begin，则说明左侧还有元素需要排序，将 begin 和 mini - 1 入栈。
    6. 栈的特性：由于栈是后进先出（LIFO）的数据结构，所以先入栈的是右侧区间，后入栈的是左侧区间，这样在出栈时，会先处理左侧区间，再处理右侧区间。
    7. 销毁栈：循环结束后，销毁栈。

    这种非递归实现的快速排序算法利用了栈的特性来避免递归调用，从而减少了函数调用的开销，并且在处理大数据集时，可以避免递归深度过大导致的栈溢出问题。

  • 相关阅读:
    STM32CubeMX外部中断
    C++重载运算符的规则
    C#的系统菜单添加自定义项 - 开源研究系列文章
    （三）DepthAI-python相关接口：OAK Nodes
    等保测评答疑
    C语言内功修炼【整型在内存中的存储】
    Java设计模式（三）结构性设计模式
    链路聚合实验（华为）
    何为擦除机制，泛型的上界？
    PID的调节
  • 原文地址：https://blog.csdn.net/Jason_from_China/article/details/139728671