-
Rust 实战丨绘制曼德博集
曼德博集
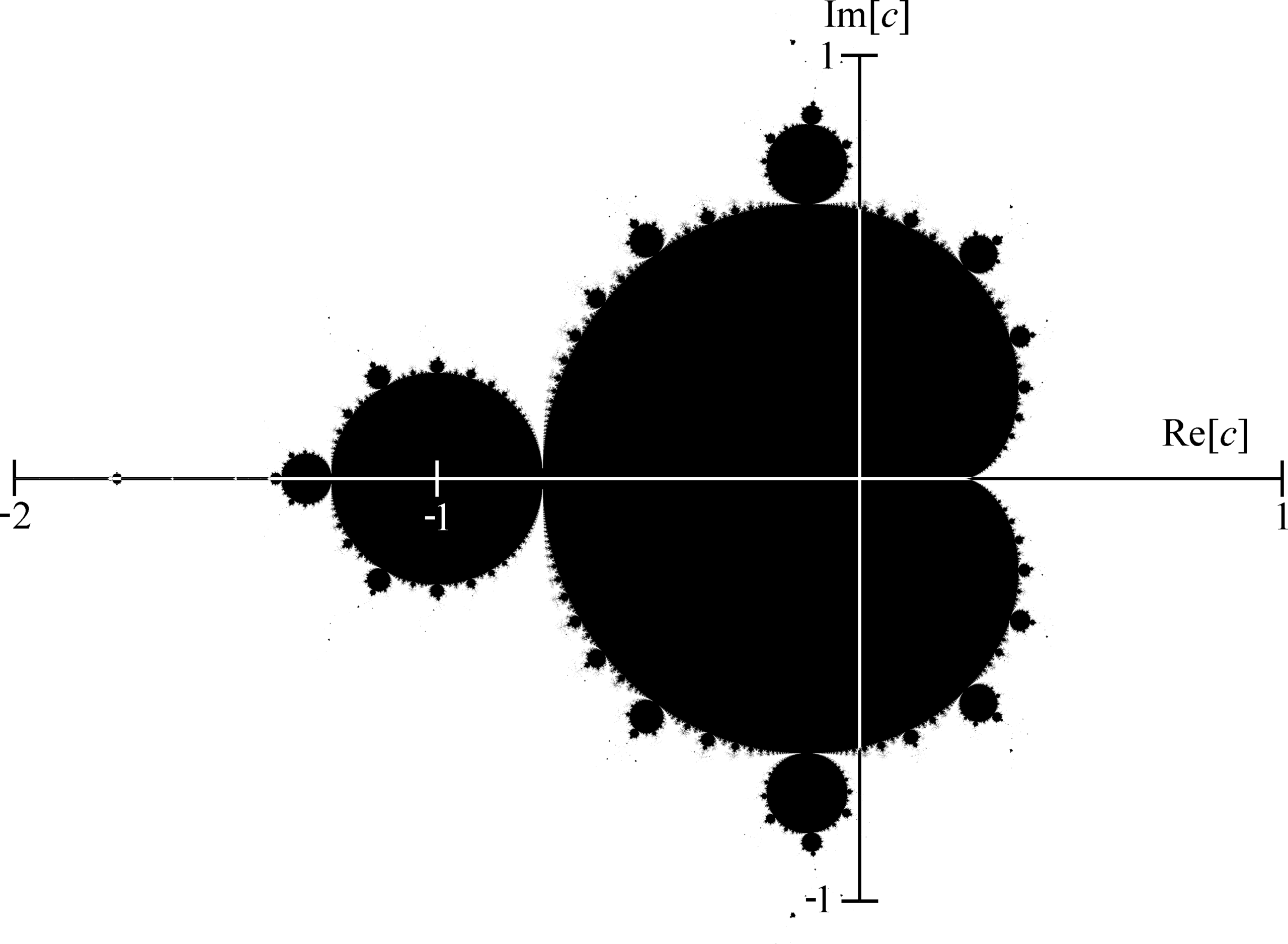
曼德博集其实是一个“没什么用”的发现。
曼德博集(Mandelbrot Set)是一种在复平面上形成独特且复杂图案的点的集合。这个集合是以数学家本华·曼德博(Benoit Mandelbrot)的名字命名的,他在研究复杂结构和混沌理论时发现了这个集合。曼德博集是分形几何的一个经典例子,显示了一个简单的数学公式如何能产生无限复杂和美丽的图案。
曼德博集的定义相对简单。对于每一个复数 c c c,我们考虑以下迭代序列:
Z n + 1 = z n 2 + c 其中 ( z 0 = 0 ) Z_{n+1} = z_n^2 + c \;\;\\ 其中 \;\; (z_0 = 0) Zn+1=zn2+c其中(z0=0)
曼德博集合由那些使得上述序列不趋于无限大的复数 c c c 组成。在复平面上,这些点形成了一种独特的图案,通常以一种美丽且艺术的方式呈现。这个图案的边界非常复杂,包含了无限的细节和自相似的结构。这意味着无论你放大图案的哪一部分,你都会发现越来越精细的结构,这些结构在形式上与整体图案相似。曼德博集合不仅在数学上有意义,也在艺术和科学中有广泛的应用,尤其是在研究混沌理论和复杂系统时。
具体可以看
目标功能
最终我们将实现一个命令行工具,它会根据我们输入的参数生成曼德博集图,使用如下:
./mandelbrot <FILE> <PIXELS> <UPPERLEFT> <LOWERRIGHT>FILE: 曼德博集图生成的图片路经。PIXELS: 图片分辨率,如4x3。UPPERLEFT: 指定在复平面中图片覆盖的左上角,如4.0,3.0。LOWERRIGHT: 制定在复平面中图片覆盖的右下角。
所以我们最终会根据指定的图片范围,截取
PIXELS分辨率大小的曼德博集图: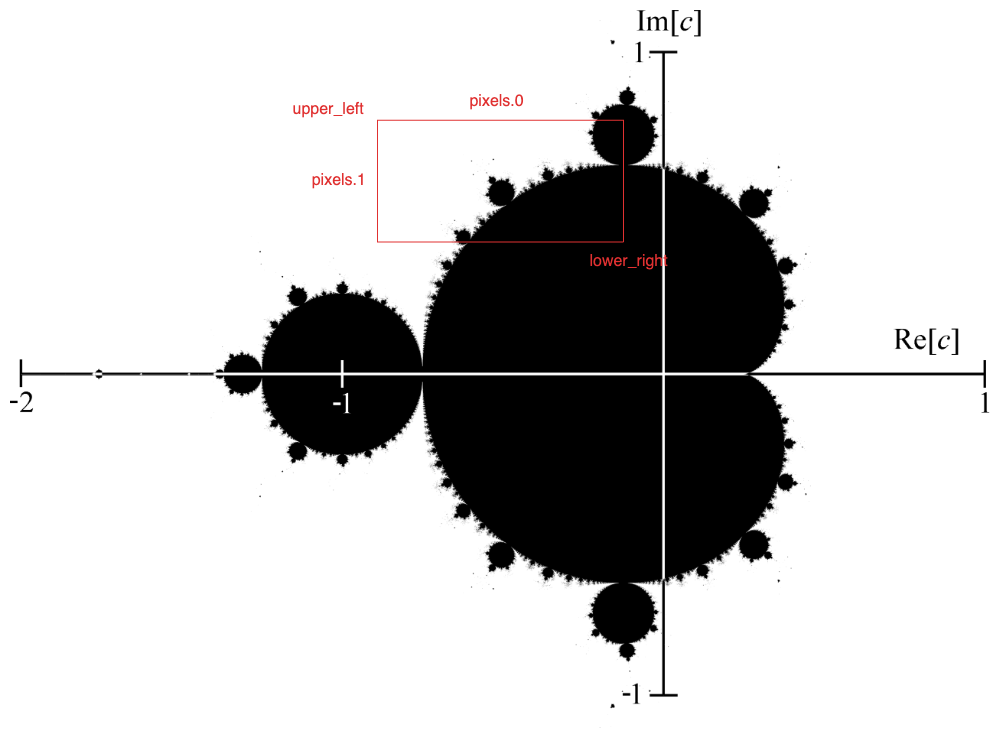
基于以上目标,我们拆分成几个问题:
- 如何表示复数?
- 如何解析分辨率和坐标?
- 如何将图上像素映射到复数?
- 如何生成曼德博集图?即如何找到那些符合曼德博集的点,并将其进行着色标注?
- 如何写入图片文件?
- 如何渲染曼德博集?
- 如何解析命令行参数?
- 如何并发写入图片文件?
能学到什么
- 曼德博集是什么?
- Rust 中的复数的原理与应用。
- Rust 泛型初探。
- Rust 中的 Option 和 Result 初探。
- Rust 并发初探。
- Rust 中如何解析命令行参数?
- Rust 如何写入图像文件?
- Rust 如何写测试用例?
- Rust 实用 crate
num、image、crossbeam。
版本
[package] name = "mandelbrot" version = "0.1.0" edition = "2021" [dependencies] image = {version = "0.13.0", features = ["default", "png"]} num = "0.4.1" crossbeam = "0.8" rayon = "1.10.0"完整代码:https://github.com/hedon-rust-road/mandelbrot/blob/master/src/main.rs
编码实现
0. 创建项目
cargo new mandelbrotcd mandelbrot1. 复数表示
使用复数,我们需要引入一个 crete:
num:cargo add num其中定义了一个复数类型
Complex:pub struct Complex<T> { /// 复数的实部 pub re: T, /// 复数的虚部 pub im: T, }这里
T是 Rust 中的泛型功能,表示任意类型T,确定好这个结构体的T的类型后,其中的属性re和im的类型也就随之确定了。2. 解析分辨率和坐标
- 分辨率格式为:4000x3000
- 坐标格式为:-1.0,2.0
2.1 解析数对
我们要做的就是,将分辨率拆成 (4000,3000),将坐标拆为 (-1.0, 2.0)。这里:
- 带解析的元素
s是一个字符串&str。 - 分隔符
separator是一个字符char。 - 返回值是一个元组
(T, T),其中T这里可以是 u64/f32 等数字,它们都需要能从字符串转化而来,即 - 因为解析可能出错,所以我们使用
Option来承载。
/// 把字符串 `s`(形如 `"400×600"` 或 ``"1.0,0.5")解析成一个坐标对 /// /// 具体来说,`s` 应该具有的格式,其中 是由`separator` 和 /// `separator` 必须是 ASCII 字符 /// /// 如果 `s` 具有正确的格式,就返回 `Some(x,y)`,否则返回 `None` fn parse_pair<T: FromStr>(s: &str, separator: char) -> Option<(T, T)> { match s.find(separator) { None => None, Some(index) => match (T::from_str(&s[..index]), T::from_str(&s[index + 1..])) { (Ok(l), Ok(r)) => Some((l, r)), _ => None, }, } }是可以被 `T:from_str` 解析的字符串。 我们可以写几个测试用例来验证一下这个函数的正确性,这里我们用到
#[test]和assert_eq!:#[test] fn test_parse_pair() { assert_eq!(parse_pair::<i32>("", ','), None); assert_eq!(parse_pair::<i32>("10,", ','), None); assert_eq!(parse_pair::<i32>(",10", ','), None); assert_eq!(parse_pair::<i32>("10,20", ','), Some((10, 20))); assert_eq!(parse_pair::<i32>("10,20xy", ','), None); assert_eq!(parse_pair::<f64>("0.5x", 'x'), None); assert_eq!(parse_pair::<f64>("0.5x1.5", 'x'), Some((0.5, 1.5))); }2.2 转为复数
我们需要的参数
upper_left和lower_right都是复平面中的一个点,所以从字符串中将数对解析完毕后,我们将其赋值到复数的实部和虚部,转为复数实例。// 把一对用逗号隔开的浮点数解析为复数 fn parse_complex(s: &str) -> Option<Complex<f64>> { match parse_pair(s, ',') { Some((re, im)) => Some(Complex { re, im }), None => None, } }3. 将像素点映射成复数
第 2 步我们其实确定了两件事:
- 确定截取曼德博集的哪一部分。
- 要在这个部分中画多少个点。
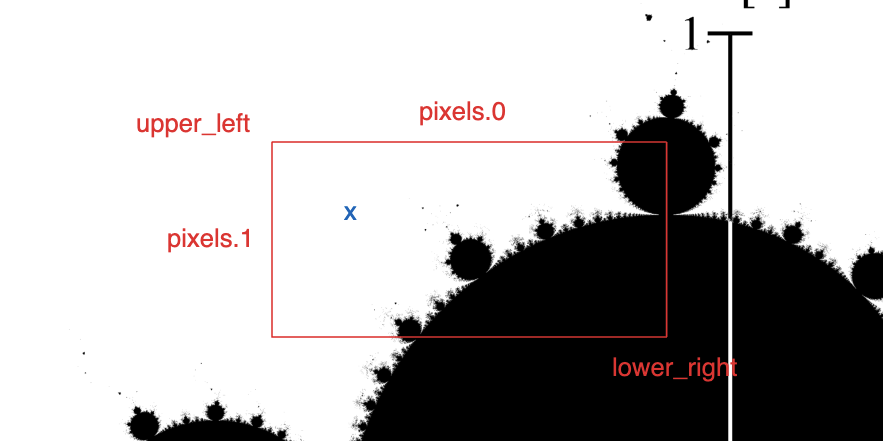
这一步我们需要把
x点转为复数,即确定它的横坐标和纵坐标。这部分可能需要发挥一下你的几何数学能力了(🤡🤡🤡)。/// 给定输出图像重像素的行和列,返回复平面中对应的坐标 /// /// `pixed` 是表示给图片中特定像素的 (column, row) 二元组。 /// `upper_left` 参数和 `lower_right` 参数是在复平面中表示指定图像覆盖范围的点。 fn pixed_to_point( /* ·--------------------> bounds.0 re 丨 丨 丨 bounds.1 im */ bounds: (usize, usize), pixed: (usize, usize), upper_left: Complex<f64>, lower_right: Complex<f64>, ) -> Complex<f64> { let (width, height) = ( lower_right.re - upper_left.re, // 右-左 upper_left.im - lower_right.im, // 上-下 ); Complex { re: upper_left.re + pixed.0 as f64 * width / bounds.0 as f64, im: upper_left.im - pixed.1 as f64 * height / bounds.1 as f64, } } #[test] fn test_pixed_to_point() { assert_eq!( pixed_to_point( (100, 200), (25, 175), Complex { re: -1.0, im: 1.0 }, Complex { re: 1.0, im: -1.0 } ), Complex { re: -0.5, im: -0.75, } ); }4. 寻找曼德博集点
什么是曼德博集点?看看上面的定义:曼德博集合由那些使得上述序列不趋于无限大的复数 c c c 组成。
现在我们可以来表示上述的公式 Z n + 1 = z n 2 + c Z_{n+1} = z_n^2 + c Zn+1=zn2+c 了:
fn complex_square_add_loop(c: Complex<f64>) { let mut z = Complex { re: 0.0, im: 0.0 }; loop { z = z * z + c } }其中我们将泛型结构体
Complex的T确定为f64,并使用loop关键字进行无限循环。所以我们的目标是什么?找到令
z不会“飞到”无穷远的c。由于复数 c c c 具有实部 re 和虚部 im,因此可以把它们视为笛卡尔平面上某个点的 x 坐标和 y 坐标,如果 c c c 在曼德博集中,就在其中用黑色着色,否则就用浅色。因此,对于图像中的每个像素,必须在复平面上相应点位运行前面的循环,看看它是否逃逸到无穷远还是永远绕着原点运行,并相应将其着色。
无限循环肯定是不现实的,我们总要找到退出循环的机会,有 2 个思路:
- 进行有限次数的迭代,这样可以获得该集合的一个不错的近似值,迭代的次数取决了精度的需要;
- 业界已证明,一旦
z离开了以原点为中心的半径 2 的圆,它最终一定会“飞到”无穷远。
所以我们最终确定的函数如下,其中
norm_sqr()会返回z跟复平面原点的距离的平方:/// 尝试测试 `c` 是否位于曼德博集中,使用最多 `limit` 次迭代来判定 /// /// 如果 `c` 不是集合成员之一,则返回 `Some(i)`,其中 `i` 是 `c` 离开以原点 /// 为中心的半径为 2 的圆时所需的迭代次数。如果 `c` 似乎是集群成员之一(确 /// 切而言是达到了迭代次数限制但仍然无法证明 `c` 不是成员),则返回 `None` fn escape_time(c: Complex<f64>, limit: usize) -> Option<usize> { let mut z = Complex { re: 0.0, im: 0.0 }; for i in 0..limit { if z.norm_sqr() > 4.0 { return Some(i); } z = z * z + c } None }5. 写入图片文件
我们可以使用
image这个 crate 来写入图片文件,它支持多种格式图片的读写,并内置了多种颜色色值。这里我们准备生成 png 图片,且需要对图片进行不同颜色的着色,所以我们引入
default和png这两个 feature。cargo add image --features default,png5.1 创建文件 File::create()
我们可以用标准库中的
File::create(filename)来创建一个文件,成功的话会返回一个文件句柄:let output = File::create(filename)?;5.2 写入图片 PNGEncoder
image中提供了PNGEncoder用于写入 png 图片,它有两个核心方法:impl<W: Write> PNGEncoder<W> { /// Create a new encoder that writes its output to ```w``` pub fn new(w: W) -> PNGEncoder<W> { PNGEncoder { w: w } } /// Encodes the image ```image``` /// that has dimensions ```width```and ```height``` /// and ```ColorType``````c``` pub fn encode(self, data: &[u8], width: u32, height: u32, color: ColorType) -> io::Result<()> { let (ct, bits) = color.into(); let mut encoder = png::Encoder::new(self.w, width, height); encoder.set(ct).set(bits); let mut writer = try!(encoder.write_header()); writer.write_image_data(data).map_err(|e| e.into()) } }new(w): 传进目标 writer,即我们上面创建的output。encode(): 写入图片信息,这里有几个参数:width: u32: 图片宽度。height: u32: 图片高度。color: ColorType: 颜色类型,可以是 RGB, Gray(8) 等。data: &[u8]: 像素色值列表,它的长度应该由上面 3 个字段共同决定,如果选取的颜色是 RGB,意味着需要 3 个 u8 才能表示一个像素点的颜色,所以长度为 width * height * 3,如果选取的颜色是 Gray(8),那么我们用 1 个 u8 就可以表示一个像素点的灰度值,所以长度为 width * height * 1。本文中我们会采用 Gray(8) 来汇总曼德博集的黑白图。
6. 渲染曼德博集
这一步我们需要来确定上述
PNGEncoder::encode()的 4 个参数:-
width: u32: 图片宽度由命令行参数中指定即可。 -
height: u32: 图片高度由命令行参数中指定即可。 -
color: ColorType: 本文我们只绘制黑白图,这里使用ColorType::Gray(8),它表示图像是一个灰度(单色)图像,每个像素用8位(即1个字节)来表示。在这种格式中,每个像素的灰度值范围是 0 到 255,其中 0 通常表示黑色,255 表示白色,中间值表示不同的灰度。 -
data: &[u8]: 像素色值列表,我们需要确定 width * height 个像素的灰度值。首先我们根据第 3 步将像素点映射成复数 c c c,然后使用第 4 步中的
escape_time()函数来判断复数 c c c 是否位于曼德博集中,如果是,则着黑色,即赋值0,如果不是,则看它迭代了多少次才失败,次数越多,则越接近曼德博集,颜色越深,即越靠近 0,所以赋值255-time。
最终我们实现的函数如下:
/// 将曼德博集对应的矩形渲染到像素缓冲区中 /// /// `bounds` 参数会给缓冲区 `pixels` 的宽度和高度,此缓冲区的每个字节都 /// 包含一个灰度像素。`upper_left` 和 `lower_right` 参数分别指定了 /// 复平面中对应于像素缓冲区左上角和右上角的点。 fn render( pixels: &mut [u8], bounds: (usize, usize), upper_left: Complex<f64>, lower_right: Complex<f64>, ) { assert_eq!(pixels.len(), bounds.0 * bounds.1); for raw in 0..bounds.1 { for column in 0..bounds.0 { let point = pixed_to_point(bounds, (column, raw), upper_left, lower_right); pixels[raw * bounds.0 + column] = match escape_time(point, 255) { None => 0, Some(count) => 255 - count as u8, } } } }7. 解析命令行参数
核心逻辑部分到这里其实就完成了,现在我们要做最后一步,就是解析命令行参数,让程序可以根据我们的要求绘制曼德博集图。
7.1 解析 std::env::args()
在 Rust 中解析命令行参数的一个常用方法是使用
std::env::args函数,这个函数返回一个迭代器,它包含了命令行上传递给程序的所有参数。对于更复杂的命令行参数解析,可以使用像clap或structopt这样的第三方库,这些库提供了更高级的功能和更好的错误处理。下面是一个使用
std::env::args的基本例子:use std::env; fn main() { let args: Vec<String> = env::args().collect(); for arg in args.iter() { println!("{}", arg); } }7.2 基础版程序
到这里,我们就可以实现完整的基础版程序了。
fn main() { // 读取参数 let args: Vec<String> = env::args().collect(); // 参数个数 = 1 + 4,其中第 1 个是应用程序名 if args.len() != 5 { eprintln!("Usage: {} FILE PIXELS UPPERLEFT LOWERRIGHT", args[0]); eprintln!( "Example: {} mandel.png 1000x700 -1.20,0.35 -1,0.20", args[0] ); std::process::exit(1); } // 解析参数 let bounds = parse_pair(&args[2], 'x').expect("error parsing image dimensions"); let upper_left = parse_complex(&args[3]).expect("error parsing upper left corner point"); let lower_right = parse_complex(&args[4]).expect("error parsing lower right corner point"); let mut pixels = vec![0; bounds.0 * bounds.1]; // 渲染曼德博集 render(&mut pixels, bounds, upper_left, lower_right); // 输出图片 write_image(&args[1], &pixels, bounds).expect("error writing PNG file"); }我们在项目根目录下编译一下程序:
cargo build --release会在 target/release 下生成可执行文件,执行:
./target/release/mandelbrot mandel.png 4000x3000 -1.20,0.35 -1,0.20执行后你应该可以看到我们生成的曼德博集图如下:

大概是处于这个位置:
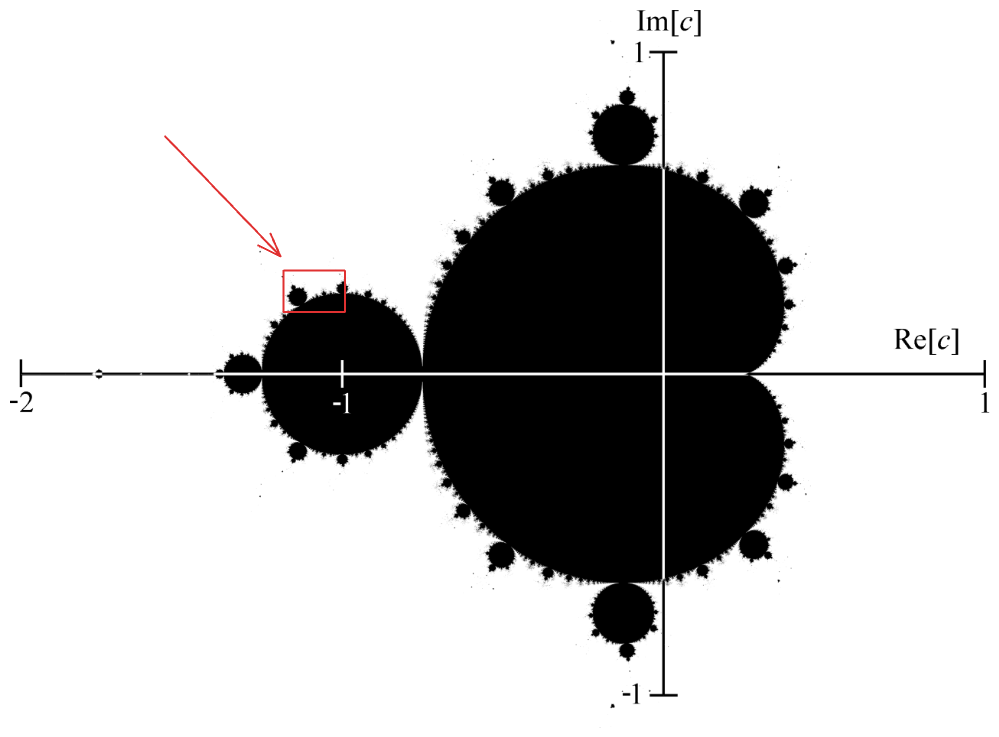
8. 并发渲染
在 macOS 或 linux 系统下,我们可以使用
time来输出程序的执行时间:time ./target/release/mandelbrot mandel.png 4000x3000 -1.20,0.35 -1,0.20 ./target/release/mandelbrot mandel.png 4000x3000 -1.20,0.35 -1,0.20 3.30s user 0.01s system 98% cpu 3.341 total笔者使用的电脑为 macbook Pro m2 max 芯片 32 G 内存 12 核,可以看到在单核模式下,差不多需要 3~4s 的时间。
几乎所有的现代机器都有多个处理器核心,而当前这个程序只使用了一个。如果可以把此工作分派个机器提供的多个处理器核心,则应该可以更快地画完图像。
为此,我们可以将图像划分成多个部分,每个处理器负责其中的一个部分,并让每个处理器为分派给它的像素着色。为简单起见,可以将其分成一些水平条带,如下图所示:

crossbeam 是 Rust 中的一个并发编程工具箱,它广泛用于提供各种并发和多线程编程的组件。
crossbeam::scope是 crossbeam 提供的一个非常有用的功能,它允许你安全地创建临时的线程,并确保这些线程在离开作用域之前结束。这里我们引入 crossbeam:
cargo add crossbeam我们将
fn main()中的:render(&mut pixels, bounds, upper_left, lower_right);替换成:
// 使用 8 个线程来并发执行 let threads = 8; // 计算每个线程负责渲染的高度,向上取整 let rows_per_band = bounds.1 / threads + 1; { // chunks_mut() 会返回一个迭代器,该迭代器会生成此缓冲区的可变且不可迭代的切片 let bands: Vec<&mut [u8]> = pixels.chunks_mut(rows_per_band * bounds.0).collect(); // crossbeam::scope 确保所有子线程在作用域结束之前完成, // 这防止了悬垂指针和其他数据竞争问题。 crossbeam::scope(|spawner| { // 遍历像素缓冲区的各个条带, // 这里 into_iter() 迭代器会为循环体的每次迭代赋予独占一个条带的所有权, // 确保一次只有一个线程可以写入它。 for (i, band) in bands.into_iter().enumerate() { // 确定每个条带的参数 let top = rows_per_band * i; let height = band.len() / bounds.0; let band_bounds = (bounds.0, height); let band_upper_left = pixed_to_point(bounds, (0, top), upper_left, lower_right); let band_lower_right = pixed_to_point(bounds, (bounds.0, top + height), upper_left, lower_right); // 创建一个线程,渲染图像 // move 表示这个闭包会接手它所用遍历的所有权, // 所以只有此闭关,即只有此线程可以使用可变切片 band。 spawner.spawn(move |_| { render(band, band_bounds, band_upper_left, band_lower_right); }); } }) .unwrap(); }再次执行:
time ./target/release/mandelbrot mandel.png 4000x3000 -1.20,0.35 -1,0.20 ./target/release/mandelbrot mandel.png 4000x3000 -1.20,0.35 -1,0.20 3.57s user 0.01s system 335% cpu 1.067 total可以看到虽然总共使用的 CPU 时间还是 3~4s,但是整个程序的执行时间只缩短到 1s 左右了。
9. rayon 工作窃取
前面我们使用 8 个工作线程优化了曼德博集的绘制速度,大概是 4 倍的速度提升。其实这还不够快。
问题的根源在于我们没有平均分配工作量。计算图像的一个像素相当于运行一个循环。事实上,图像的浅灰色部分(循环会快速退出的地方)比黑色部分(循环会运行整整 255 次迭代的地方)渲染速度要快得多。因此,虽然我们将整个区域划分成了大小相等的水平条带,但创建了不均等的工作负载,

使用 rayon 很容易解决这个问题。我们可以为输出中的每一行像素启动一个并行任务。这会创建数百个任务,而 rayon 可以在其线程中分配这些任务。有了工作窃取机制,任务的规模是无关紧要的。rayon 会对这些工作进行平衡。
我们先引入
rayon:cargo add rayon在
main.rs中引入rayon:use rayon::prelude::*;然后
main中并发绘制的部分替换为下面的代码:let bands: Vec<(usize, &mut [u8])> = pixels.chunks_mut(bounds.0).enumerate().collect(); bands.into_par_iter().for_each(|(i, band)| { let top = i; let band_bounds = (bounds.0, 1); let band_upper_left = pixed_to_point(bounds, (0, top), upper_left, lower_right); let band_lower_right = pixed_to_point(bounds, (bounds.0, top + 1), upper_left, lower_right); render(band, band_bounds, band_upper_left, band_lower_right); });首先,创建 bands,也就是要传给 rayon 的任务集合。每个任务只是一个元组类型 (usize, &mut [u8]):第一个是计算所需的行号,第二个是要填充的 pixels 切片。我们使用 chunks_mut 方法将图像缓冲区分成一些行,enumerate 则会给每一行添加行号,然后 collect 会将所有数值切片对放入一个向量中。(这里需要一个向量,因为 rayon 只能从数组和向量中创建并行迭代器。)
编译:
cargo build --release再次执行:
time ./target/release/mandelbrot mandel.png 4000x3000 -1.20,0.35 -1,0.20 ./target/release/mandelbrot mandel.png 4000x3000 -1.20,0.35 -1,0.20 3.96s user 0.01s system 973% cpu 0.408 total可以看到,这次速度提升更加明显,总共只用了 0.4s 左右的时间。
以上就是实用 Rust 绘制曼德博集实战的全部内容,enjoy,happy coding~
-
相关阅读:
java 基础语法
安信可IDE(AiThinker_IDE)编译ESP8266工程方法
R语言拟合ARIMA模型并使用拟合模型进行预测推理、使用autoplot函数可视化ARIMA模型预测结果、可视化包含置信区间的预测结果
java毕业设计项目struts实现的图书馆管理系统|图书借阅[包运行成功]
C++ 函数修改指针指向__fun(int *&pointer)
uniapp:使用百度API提取身份证信息(微信小程序适用)
supOS APP开发者课程练习册
计算机操作系统详解
Hive面试题系列第七题-同时在线问题
【数据库系统概论】第九章关系查询处理何查询优化
- 原文地址:https://blog.csdn.net/Hedon954/article/details/139676109