Meta Llama 3 RMSNorm（Root Mean Square Layer Normalization）

Meta Llama 3 RMSNorm（Root Mean Square Layer Normalization）

flyfish

先看LayerNorm和BatchNorm

展示计算的方向

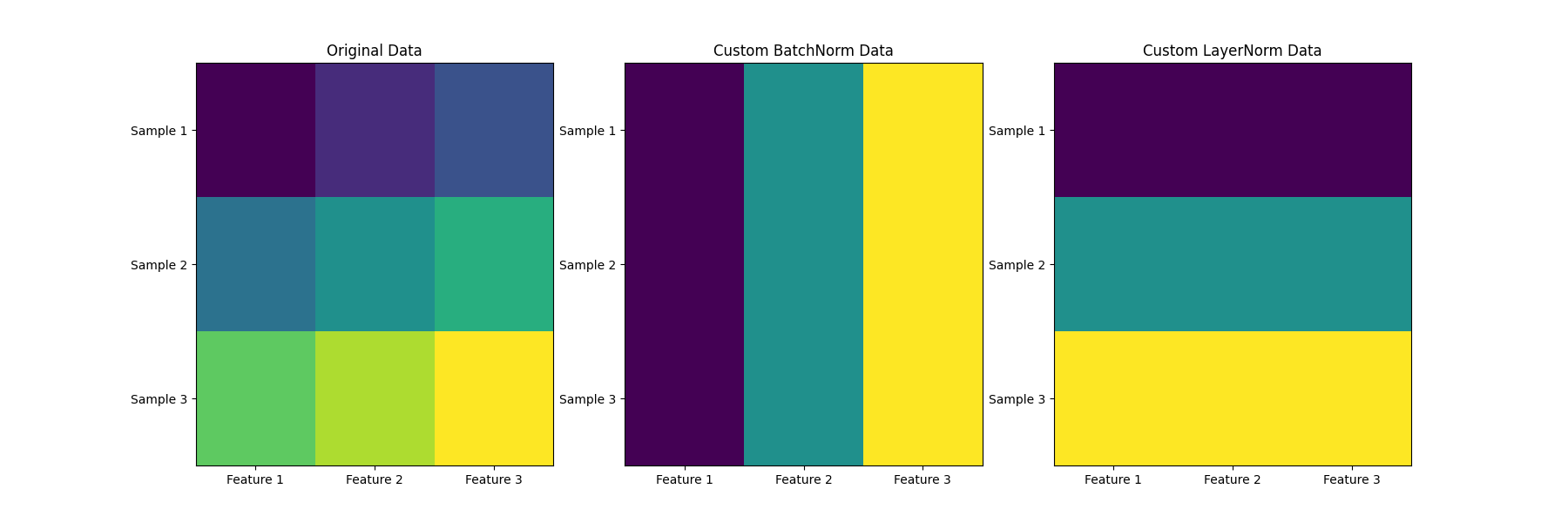
• axis=0 代表第一个轴，逐列处理数据。
• axis=1 代表第二个轴，逐行处理数据。在二维数组中，axis=-1 等同于 axis=1。
• axis=-1 代表最后一个轴。在二维数组中，axis=-1 等同于 axis=1，即最后一个轴。

在二维的情况 下，BatchNorm是按列算，LayerNorm按行算

import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn

class CustomLayerNorm:
    def __init__(self, eps=1e-5):
        self.eps = eps

    def __call__(self, x):
        mean = np.mean(x, axis=-1, keepdims=True)
        std = np.std(x, axis=-1, keepdims=True)
        normalized = (x - mean) / (std + self.eps)
        return normalized

class CustomBatchNorm:
    def __init__(self, eps=1e-5):
        self.eps = eps

    def __call__(self, x):
        mean = np.mean(x, axis=0)
        std = np.std(x, axis=0)
        normalized = (x - mean) / (std + self.eps)
        return normalized

# Original Data
data = np.array([[1.0, 2.0, 3.0],
                 [4.0, 5.0, 6.0],
                 [7.0, 8.0, 9.0]])

# Apply Custom LayerNorm
custom_layer_norm = CustomLayerNorm()
custom_layer_norm_data = custom_layer_norm(data)

# Apply Custom BatchNorm
custom_batch_norm = CustomBatchNorm()
custom_batch_norm_data = custom_batch_norm(data)

# Apply PyTorch LayerNorm
data_tensor = torch.tensor(data, dtype=torch.float32)
layer_norm = nn.LayerNorm(data_tensor.size()[1:])
pytorch_layer_norm_data = layer_norm(data_tensor).detach().numpy()

# Compare Custom and PyTorch LayerNorm
print("Original Data:\n", data)
print("Custom LayerNorm Data:\n", custom_layer_norm_data)
print("PyTorch LayerNorm Data:\n", pytorch_layer_norm_data)

Original Data:
 [[1. 2. 3.]
 [4. 5. 6.]
 [7. 8. 9.]]
Custom LayerNorm Data:
 [[-1.22472987  0.          1.22472987]
 [-1.22472987  0.          1.22472987]
 [-1.22472987  0.          1.22472987]]
PyTorch LayerNorm Data:
 [[-1.2247356  0.         1.2247356]
 [-1.2247356  0.         1.2247356]
 [-1.2247356  0.         1.2247356]]

举个例子计算 LayerNorm

具体步骤如下：

1. 计算每行的均值：

• 对每一行，计算其均值。
• 第1行: mean = (1 + 2 + 3) / 3 = 2
• 第2行: mean = (4 + 5 + 6) / 3 = 5
• 第3行: mean = (7 + 8 + 9) / 3 = 8

2. 计算每行的标准差：

• 对每一行，计算其标准差。
• 第1行: $std=sqrt(((1-2{)}^2+(2-2{)}^2+(3-2{)}^2)/3)=sqrt((1+0+1)/3)=sqrt(2/3)\approx 0.8165$
• 第2行: $std=sqrt(((4-5{)}^2+(5-5{)}^2+(6-5{)}^2)/3)=sqrt((1+0+1)/3)=sqrt(2/3)\approx 0.8165$
• 第3行: $std=sqrt(((7-8{)}^2+(8-8{)}^2+(9-8{)}^2)/3)=sqrt((1+0+1)/3)=sqrt(2/3)\approx 0.8165$

3. 标准化每一行：

• 对每一行，使用均值和标准差进行标准化。公式为：$(x-mean)/(std+eps)$。其中 eps 是一个小常数，防止除零，通常取值为 1e-5。
• 计算结果如下：

标准化公式: $normalized=(x-mean)/(std+eps)$

第1行: 
[(1-2)/(0.8165+1e-5), (2-2)/(0.8165+1e-5), (3-2)/(0.8165+1e-5)]
= [-1.2247, 0, 1.2247]

第2行: 
[(4-5)/(0.8165+1e-5), (5-5)/(0.8165+1e-5), (6-5)/(0.8165+1e-5)]
= [-1.2247, 0, 1.2247]

第3行: 
[(7-8)/(0.8165+1e-5), (8-8)/(0.8165+1e-5), (9-8)/(0.8165+1e-5)]
= [-1.2247, 0, 1.2247]

最终标准化结果矩阵为：

[[-1.2247, 0, 1.2247]
 [-1.2247, 0, 1.2247]
 [-1.2247, 0, 1.2247]]

RMSNorm 的整个计算过程

Meta Llama 3 使用了RMSNorm
假设我们有以下 2D 输入张量 $X$（为了简单起见，我们假设这个张量有 2 行 3 列）：
$$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\end{array}\right]$$
RMSNorm 的计算过程如下：

1. 计算每行的均方根 (RMS)：
   首先，对于每一行，我们计算该行元素的平方和的均值，然后取其平方根。
   对于第 1 行：
   $${\text{RMS}}_{\text{row1}}=\sqrt{\frac{1^2+2^2+3^2}{3}}=\sqrt{\frac{1+4+9}{3}}=\sqrt{4.67}\approx 2.16$$
   对于第 2 行：
   $${\text{RMS}}_{\text{row2}}=\sqrt{\frac{4^2+5^2+6^2}{3}}=\sqrt{\frac{16+25+36}{3}}=\sqrt{25.67}\approx 5.07$$
2. 使用均方根对输入进行归一化：
   将每行的元素除以该行的 RMS 值。这里的 epsilon 用于防止除以零的问题，我们假设 $ϵ=1e-6$。
   对于第 1 行：$${\text{Normed}}_{\text{row1}}=\left[\begin{array}{ccc}\frac{1}{2.16+ϵ}& \frac{2}{2.16+ϵ}& \frac{3}{2.16+ϵ}\end{array}\right]\approx \left[\begin{array}{ccc}0.462& 0.925& 1.387\end{array}\right]$$
   对于第 2 行：$${\text{Normed}}_{\text{row2}}=\left[\begin{array}{ccc}\frac{4}{5.07+ϵ}& \frac{5}{5.07+ϵ}& \frac{6}{5.07+ϵ}\end{array}\right]\approx \left[\begin{array}{ccc}0.789& 0.986& 1.183\end{array}\right]$$
3. 应用可学习的缩放参数：
   假设权重参数 $\text{weight}$ 为一个向量 $[1,1,1]$，表示每个元素的缩放因子。对于第 1 行：$${\text{Output}}_{\text{row1}}=\left[\begin{array}{ccc}0.462\cdot 1& 0.925\cdot 1& 1.387\cdot 1\end{array}\right]=\left[\begin{array}{ccc}0.462& 0.925& 1.387\end{array}\right]$$对于第 2 行：$${\text{Output}}_{\text{row2}}=\left[\begin{array}{ccc}0.789\cdot 1& 0.986\cdot 1& 1.183\cdot 1\end{array}\right]=\left[\begin{array}{ccc}0.789& 0.986& 1.183\end{array}\right]$$

实际代码实现

以下是使用 PyTorch 实现上述步骤的代码示例：

import torch
import torch.nn as nn

class RMSNorm(nn.Module):
    def __init__(self, dim: int, eps: float = 1e-6):
        super().__init__()
        self.eps = eps
        self.weight = nn.Parameter(torch.ones(dim))

    def _norm(self, x):
        return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)

    def forward(self, x):
        output = self._norm(x.float()).type_as(x)
        return output * self.weight

# 示例数据
data = torch.tensor([[1.0, 2.0, 3.0],
                     [4.0, 5.0, 6.0]])

# 实例化 RMSNorm 层
rms_norm = RMSNorm(dim=data.size(-1))

# 计算归一化后的输出
normalized_data = rms_norm(data)

print("Original Data:\n", data)
print("RMSNorm Normalized Data:\n", normalized_data)

结果

运行上述代码后，我们将得到归一化后的数据：

 tensor([[1., 2., 3.],
        [4., 5., 6.]])
RMSNorm Normalized Data:
 tensor([[0.4629, 0.9258, 1.3887],
        [0.7895, 0.9869, 1.1843]], grad_fn=)