二叉树的基础讲解

二叉树在遍历，查找，增删的效率上面都很高，是数据结构中很重要的，下面我们来基础的认识一下。(高级的本人还没学，下面的代码用伪代码或C语言写的)我会从树，树的一些专有名词，树的遍历，二叉树，二叉树的遍历以及后面升级的树进行一部分的介绍。

树

首先我们从最开始的树来进行讲解，我们知道链表是节点上一个连下一个形成一条长链，一个节点只能连接一个节点。而我们的树就是一个节点连接多个节点，就和我们生活中的树相似，一个点可以分出很多枝干。

下面就是开头节点连接四个节点的树，而树可以有很多的节点。

那么树的结构这么复杂多变，需要理清他们的结构关系。例如A我们要叫什么，H我们要叫什么?

树的相关专业名词

这里的名词是通过日常的树的一些名词和我们人与人之间关系组合形成的。所以结合这两部分可以更好记忆。我也会结合上面的这颗树来进行举例。

这里面打勾的是比较重要的。

节点✔

节点我们在链表里面就有讲过，不多说明。这里的A B C D E F G H都是节点

根节点

根节点就是树的起点节点。这里的A就是根节点

双亲节点或父亲节点✔

一个节点的上一个节点就是他的父亲节点或双亲节点。例如A是B的父亲节点或双亲节点

孩子节点或子节点✔

一个节点的直接连接的下一个节点就是它的子节点或孩子节点。例如B C D E都是A的孩子节点或子节点

节点的度

一个节点含有子树（或者可以说孩子节点）个数就是节点的度。例如这里A的度是4，因为有B C D E四个树或者四个孩子节点。

树的度✔

根节点的度就是树的度。例如上面的这颗树的度就是4。

非终端节点或分支节点

度不为零的节点，通俗说就是有孩子的节点。这里除了F H D E都是分支节点。

兄弟节点

父亲节点是同一个的节点是兄弟节点，这里可以结合家庭关系理解并记忆。例如这里B C是兄弟，F G不是兄弟，但是是下面要说的堂兄弟节点。

节点的层次

就是节点在第几层，这里层次从上往下增长，一般定义根节点是第一层或者第零层。这里的B是第二层或者第一层（分别对应根节点的第一层和第零层）。

树的高度或深度✔

树的最大层次。如图的最大层次是4。

堂兄弟节点

双亲在同一层的节点互为堂兄弟。例如F G就是堂兄弟。

节点的祖先

从根到该节点所经分支上的所有节点。例如A是所有节点的祖先

子孙

以某节点为根的子树中任一节点都称为该节点的子孙。上如除了A的节点都是A的子孙。

森林

由m（m>0）棵互不相交的树的集合称为森林。

多叉树的遍历

因为树的节点个数不缺定，所以我们要借助其他的数据结构来存储我们一个节点的子节点。

例如我们要遍历上图的A，我们先遍历A里面的内容，然后再将A的所有节点写进栈里面，或者队列里面，然后我们进行循环，如果栈或者队列为空我们就停止循环。每次出数据的时候我们就将它的子节点全部存进这个数据结构里。这样我们就可以完成所有节点的遍历。

伪代码如此，我不会写伪代码，大概看看吧。

第二种是比较厉害的处理办法，不需要运用的任何数据结构，但是树的创建结构需要改变一下

我们将上面的树结构改成这样，我们增强层之间的联系，而亲子之间只让两个之间有联系。这样遍历的顺序就是A->B里面所有节点->C里面所有节点->D里面所有节点->E里面所有节点。这个需要用到递归来处理。这里我用C语言来写一下

首先是树的定义和树的创建，结构和上面图是一样的：

这里结构体的创建孩子的节点决定于所有节点中节点最大孩子数。

然后是遍历函数和main函数

结果也是对的

树的运用

像我们电脑、手机里面的文件夹就是一个多叉树，一个文件夹就相当于一个节点，文件夹里面的内容就是子文件夹

二叉树

二叉树是树里面特殊的一种树，每个节点的孩子节点<=2。二叉树因为只分了左右节点可以很好的控制数据关系，更好的进行相关的数据操作。

下面就是二叉树的一些主要出现的操作，如果能自主写的到这些，那么二叉树的基础部分掌握的相对牢固：

二叉树的三种特殊情况

满二叉树

设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个树，第 h 层所有的结点都连续集中在最左边，而满二叉树是完全二叉树的一种

完全二叉树

深度为k且有2^k-1个结点的二叉树

平衡二叉树

 １，左子树与右子树的高度之差的绝对值小于等于１；

 ２，左子树和右子树也是平衡二叉树．

二叉树里面的恒等式

1，叶子节点数=度为2的节点的个数+1

二叉树的遍历

二叉树的遍历是认识二叉树最重要的一点，或许大家在大学里面学习了二叉树的遍历——前中后序遍历，但是大多数人是没有真正了解三个序具体过程是怎么来的。

二叉树因为涉及多叉也是要用递归来遍历的，或者用数据结构进行存储。

我们一下面这颗二叉树来进行分析三个序。

这颗树的手工创建代码如下

前序

前序遍历遵从的是先遍历节点的内容，再遍历节点的左子树，在遍历节点的右子树。

下面进行分析：

首先声明：这颗树有点大，如果下面的分析看不懂可以先从黑体字开始看，就是A左子树B的遍历。

要遍历这颗二叉树，先要遍历A节点，那么先遍历A节点的值是'A'，然后遍历A的左子树B。遍历B先遍历它的值是'B'，然后遍历B的左子树D，遍历D先遍历值'D'，然后遍历D的左子树G，遍历G先遍历它的值'G'，然后遍历G的左子树，G的左子树是NULL，所以为空，再遍历G的右子树也是空的。G遍历完了，标志D的左子树遍历完了，我们要遍历D的右子树，右子树为NULL，D遍历完，标志B的左子树遍历完了。现在要遍历B的右子树E，欲遍历E要遍历E的值'E'，然后遍历E的左子树H，要遍历H先遍历H的值然后依次遍历左右子树都为空，那么E的左子树遍历完了遍历E的右子树I，I也是同样操作，欲遍历I先遍历I的值'I',然后遍历I的左子和右子树都为空，遍历完标志E的右子树遍历完了，就标志B的右子树遍历完了，即B树遍历完了，就标志A的左子树遍历完了。然后就要遍历A的右子树，先遍历C，先遍历C的值'C'，然后遍历C的左子树为空，然后遍历C的右子树F，先遍历F的值'F'，然后遍历F的左子树J,先遍历J的值'J'，然后遍历J左右子树都为空，然后遍历F右子树K，先遍历K的值'K'，然后遍历K的左右子树都是空，然后F遍历完，标志C的右子树遍历玩标志A的右子树遍历完。最后标志这颗树遍历完。

最终的遍历顺序是A->B->D->G->NULL->NULL->NULL->E->H->NULL->NULL->I->NULL->NULL->C->NULL->F->J->NULL->NULL->K->NULL->NULL

而我现在写的过程也是递归调用的全过程。

那么我们开始写它的递归代码:

就是这么简单，其实打印NULL的代码也不需要，但这里主要是看遍历的流程。函数的递归流程是和上面流程一模一样的。

我们也可以看到程序遍历的和我们分析出来的是一样的。

中序

中序是先遍历左子树，再遍历节点数据，再遍历右子树。

只要把前序看懂了，中序就是水到渠成的事。

依然是上面的这张图，我们再分析一下。这次我只分析A的左子树B：

要遍历B，先遍历B的左子树D，要遍历D先遍历左子树G，要遍历G先遍历G左子树为空，然后遍历G值，然后遍历G右子树，G遍历完了标志D左子树遍历完了，然后遍历D值，然后遍历D右子树为空，然后D树遍历完标志B的左子树遍历完，然后遍历B值，然后遍历B的右子树E，先遍历E的左子树H，先遍历H左子树为空，然后遍历H值，然后遍历H的右子树为空，然后H遍历完标志E的左子树遍历完了，然后遍历E值，然后E的右子树I，先遍历I左子树为空，然后遍历I值，然后遍历右子树为空，然后标志E遍历完，标志B右子树遍历完，标志B树遍历完。

A的右树你们自己来试一试，最后结果是：

NULL->G->NULL->D->NULL->B->NULL->H->NULL->E->NULL->I->NULL->A->NULL->C->NULL->J->NULL->F->NULL->K->NULL

写代码也很好写，交换一下位置就行了

后序

先遍历节点左子树，然后遍历节点右子树，然后是遍历节点的值。

后序我不会说过程了，请大家自己尝试。

答案是

NULL->NULL->G->NULL->D->NULL->NULL->H->NULL->NULL->I->E->B->NULL->NULL->NULL->J->NULL->NULL->K->F->C->A

然后是代码和运行结果:

下面我再出几个题

答案：

前：A B NULL E H NULL NULL I NULL NULL C NULL F J NULL NULL K NULL NULL

中：NULL B NULL H NULL E NULL I NULL A NULL C NULL J NULL F NULL K NULL

后：NULL NULL NULL H NULL NULL I E B NULL NULL NULL J NULL NULL K F C A

答案：

前：A B D G NULL NULL I NULL NULL NULL C H NULL NULL F J NULL NULL K NULL NULL

中：NULL G NULL D NULL I NULL B NULL A NULL H NULL C NULL J NULL F NULL K NULL

后：NULL NULL G NULL NULL I D NULL B NULL NULL H NULL NULL J NULL NULL K F C A

模拟前序(深搜)

我们在树的遍历就说到用数据结构存储节点，这里我们就来用栈来实现实现。

栈的函数就自己写或者CV一下，不会的可以看我的相关博客。

（忘记栈的销毁了，记得销毁，养成习惯）

层序(广搜)

层序就是一层一层遍历，就是按顺序遍历，那么这个按顺序我们就想到了队列。

层序我们发现了一个规律，它遍历出来的数据是一层一层从上到下从左到右遍历的，数据提现的很直观，我们可以通过结果很轻松的知道二叉树大概长什么样子，但是可能底层的数据不准确。但是完全二叉树就是一个例外，如果告诉了是完全二叉树，又告诉了它层序的结果，那么这颗树就已知了。而这个和我们堆的结构是密切相关的。

（忘记队列的销毁了，记得销毁，养成习惯）

二叉树的其他函数

这些函数也是需要会写的

这里面有几个已经写了就不写了

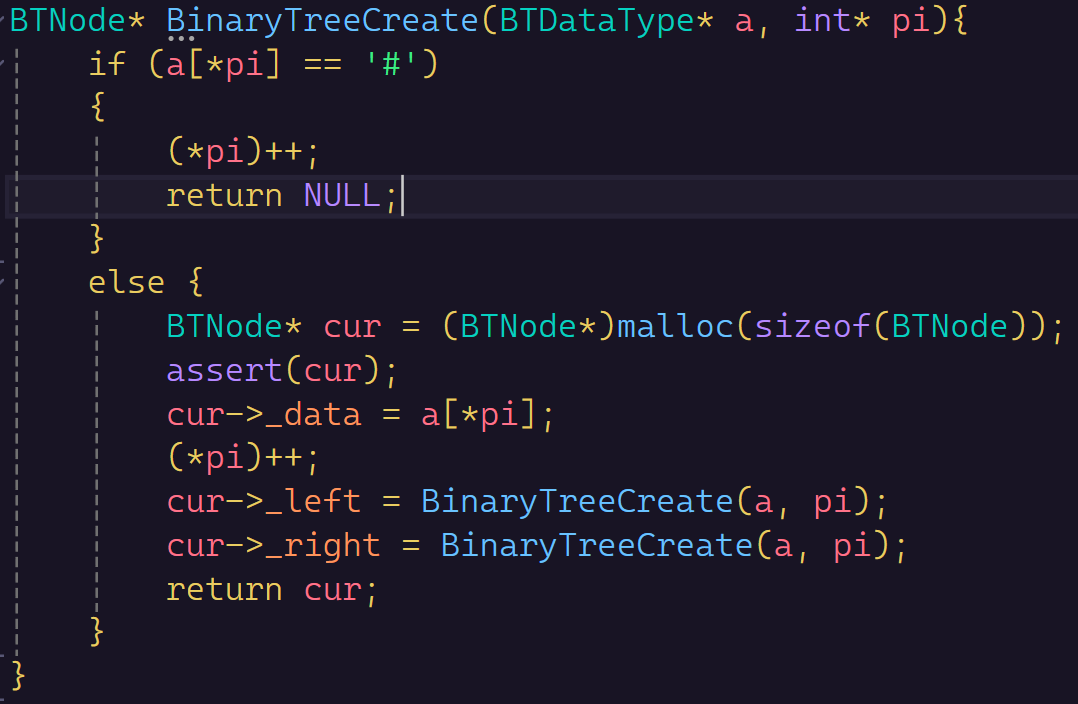
首先是二叉树的构建

二叉树销毁

二叉树节点个数

二叉树叶子节点个数

二叉树第k层节点个数

二叉树查找值为x的节点

判断二叉树是否是完全二叉树

这个需要讲一下，完全二叉树是最后一个层序值前面都不能有NUL，当出现NULL看后面还有没有NULL就行了.

普通二叉树的缺陷

我们创造二叉树最后是为了查找快速，二叉树的查找是类似于二分的，时间复杂度是logN，速度非常快。但是如果我们二叉树建立的比较特殊，所有的节点都是在上一个节点的做子树上，将会变成一条链表，时间复杂度也降为N。所以会有更高级的二叉树来弥补这个缺陷。

高级数据结构里面的树

据我现在了解后面会有平衡二叉树（AVL树），红黑树(二叉树），B树，B+树（多叉）等树。这些树我也不知道长什么样，但是可以时刻保持logN的时间复杂度。

另外这些高阶树会和哈西表进行结合，将红黑树挂到哈西表的每个格子上，让时间复杂度进一步减小。总之学习数据结构的道路还很漫长.......

求赞和关注

都看到这里了，求大家点赞关注一下吧😊