数据结构试题 20-21

 真需要就死记吧

---

---

---

 

 

二叉树遍历-先序(非递归)【图解+代码】_哔哩哔哩_bilibili

 

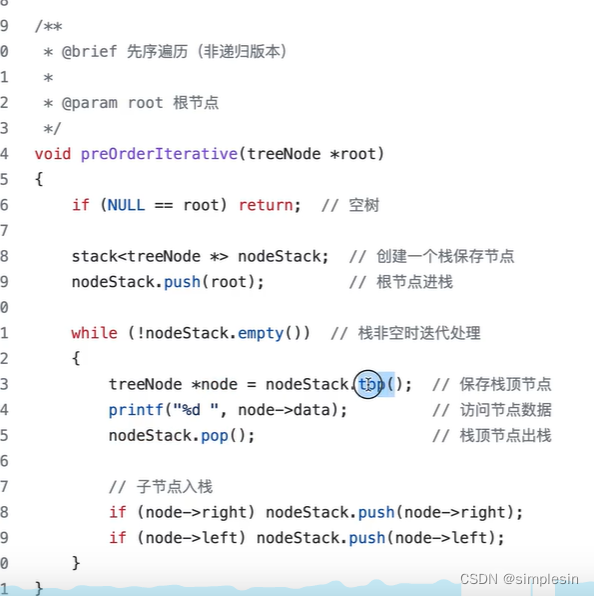
 解释一下步骤：

一个循环为：

1.取节点

2.放右子树

3.放左子树

每次循环，都要从栈里取出一个节点

先放右子树，再放左子树

那这道题就是，先放1（根节点）

然后开始循环

没东西可出

放3，放2

第一次循环结束

拿出2

放4

第二次循环结束

拿出4

放7

第三次循环结束

拿出7

没东西可放

第四次循环结束

拿出3

放6，放5

第五次循环结束

拿出5

没东西可放

第六次循环结束

拿出6

---

---

---

1、假设线性表L采用单链表存储结构，设计一个算法，在L的数据元素最大值之前插入（假设L的各个数据元素值不同）数据元素x。

基本思想，先查找到最大元素对应的结点，再在之前插入x对应的结点；

设计算法时要考虑用到两组指针变量，一组（maxp,maxpre）记录最大元素的结点及其前驱，另一组结点用来遍历各个数据元素对应的结点及其前驱，（pre,p）

void insertmaxnode(LinkNode *&L, Elemtype x)
{   LinkNode *p=L->next，*pre=L，*maxp=p，*maxpre=pre;
LinkNode *p=L->next,*pre=L; 
LinkNode *maxp=p,*maxpre=L,*s; 
while (p!=NULL) 
{ 
if (maxp->datadata) 
{ 
maxp=p; 
maxpre=pre; 
} 
pre=p; p=p->next; 
} 
s=(LinkNode *)malloc(sizeof(LinkNode)); 
s->data=x; 
s->next=maxpre->next; 
maxpre->next=s; 
}
 

---

LinkNode *p=L->next：p指向链表的第一个数据节点。

LinkNode *pre=L：pre指向头节点，用于记录p的前驱。

LinkNode *maxp=p：maxp初始化为第一个数据节点，用于记录当前最大值所在的节点。

LinkNode *maxpre=pre：maxpre初始化为头节点，用于记录最大值节点的前驱。

---

s=(LinkNode *)malloc(sizeof(LinkNode));

这行代码的作用是为新的链表节点分配内存，并将分配到的内存地址赋给指针s。这样一来，s就可以作为新节点的地址，通过它我们可以访问和操作这个新节点。

---

1. 插入新节点:

   • 在循环结束后，找到了链表中的最大值节点及其前驱。接下来，创建一个新的节点s，用于存储新插入的数据元素x：s=(LinkNode *)malloc(sizeof(LinkNode)); s->data=x;
   • 调整指针，将新节点s插入到最大值节点前：s->next=maxpre->next; maxpre->next=s;。这样，s就成为了原最大值节点的新前驱，而原最大值节点的前驱变为了s。

 

---

---

---

 

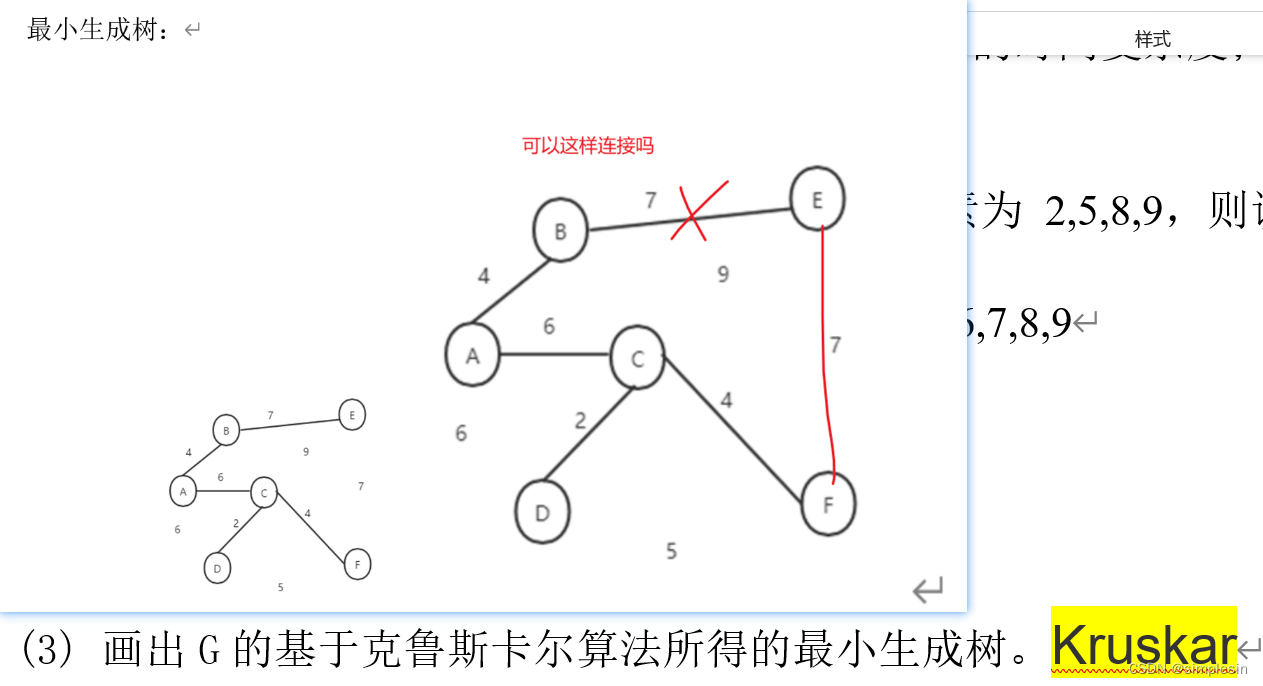
该怎么只利用二叉排序树的定义以及后续遍历序列来找出中序和前序遍历。 

---

---

---

2、假设二叉树采用二叉链存储结构，设计一个算法，求二叉树中第k层结点个数。

void Lnodenum(BTNode *b，int h，int k，int &n)

{  if (b==NULL)   //空树直接返回

      return;

   else           //处理非空树

   {  if (h==k) n++; //当前访问的结点在第k层时，n增1

      else if (h

      {  Lnodenum(b->lchild，h+1，k，n);

      Lnodenum(b->rchild，h+1，k，n);

      }

   }

}

为什么当前访问的结点在第k层时，n增1？

在这个算法中，参数b表示当前正在访问的二叉树节点，h表示该节点当前所在的层次（高度），k是要查找的层数，n是一个引用参数，用于记录在第k层的节点总数。函数的目标是计算并返回二叉树中第k层节点的个数。

当执行到条件if (h==k)时，这意味着当前访问的节点正好位于我们感兴趣的第k层。因此，如果要准确统计第k层的节点数量，每当遇到一个这样的节点，就需要将计数器n的值增加1。这是因为在二叉树的递归遍历过程中，每遇到一个节点，我们都能确切知道它处于哪一层，所以当层数匹配我们寻找的目标层数时，就应当累加计数。这样，通过遍历整棵树并应用这个逻辑，最终n中存储的就是第k层节点的总数。

 若当前结点层次小于k，递归处理左、右子树，因为说明这个结点层次不是我要求的那层