算法 java 排序和查找

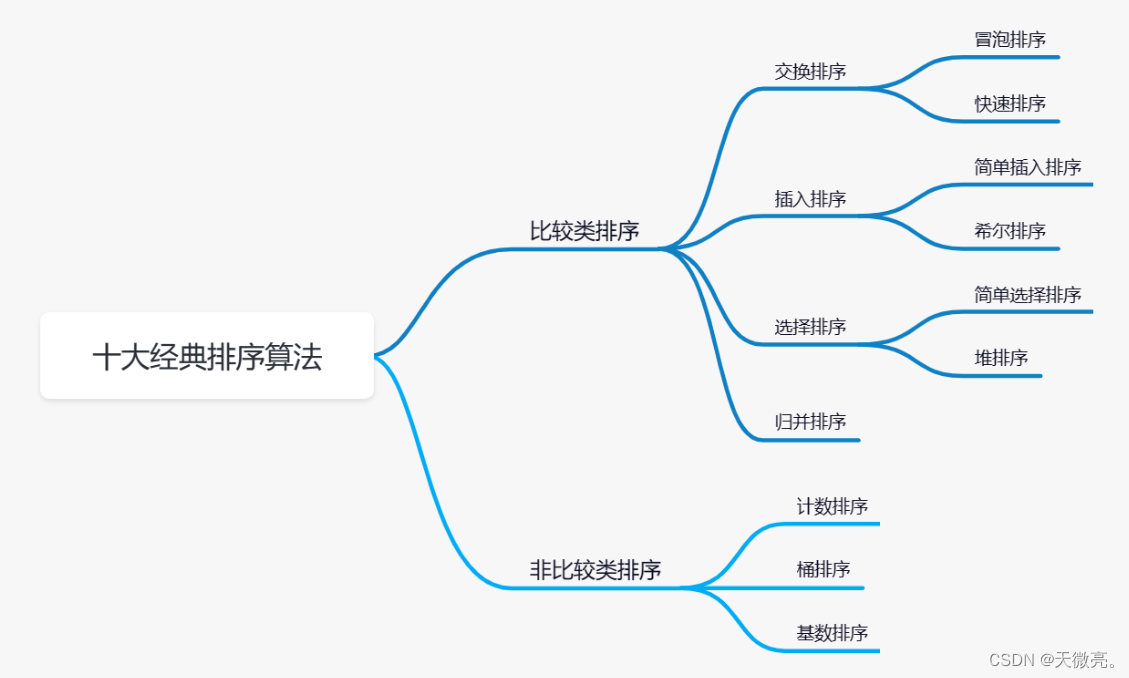
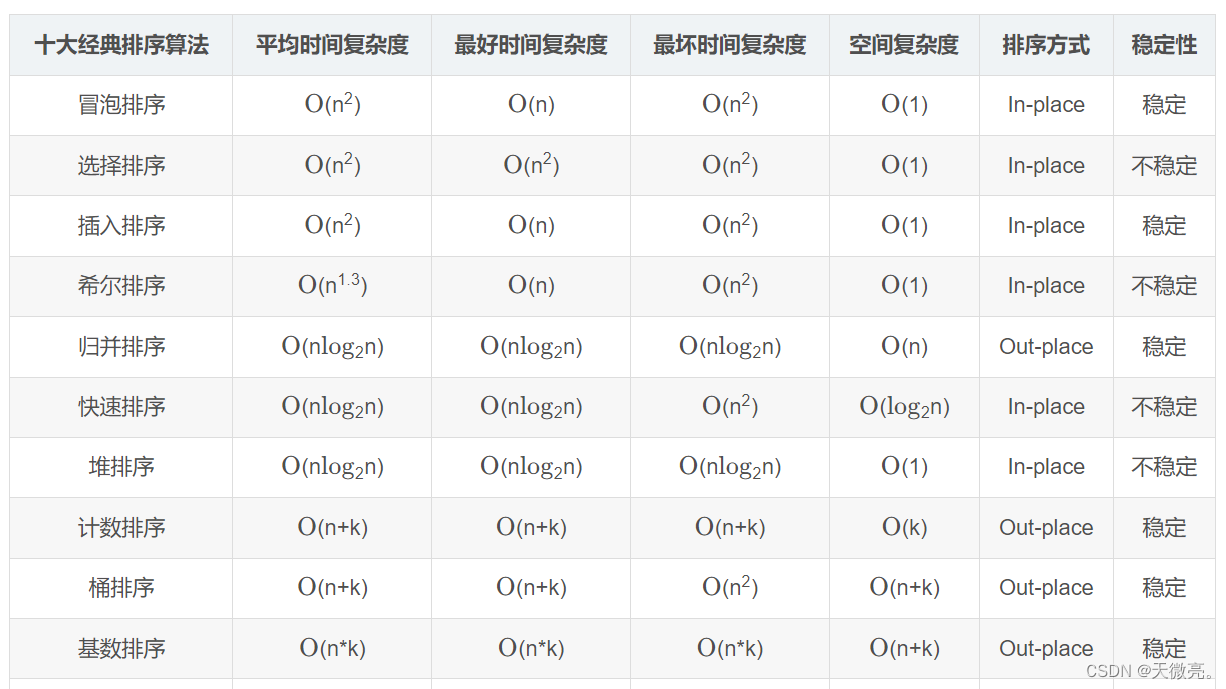
参考： 排序算法总结

冒泡排序（稳定）

经过多次迭代，通过相邻元素之间的比较与交换，使值较小的元素逐步从后面移到前面，值较大的元素从前面移到后面。

这个过程就像水底的气泡一样从底部向上「冒泡」到水面，这也是冒泡排序法名字的由来。

接下来，我们使用「冒泡」的方式来模拟一下这个过程。

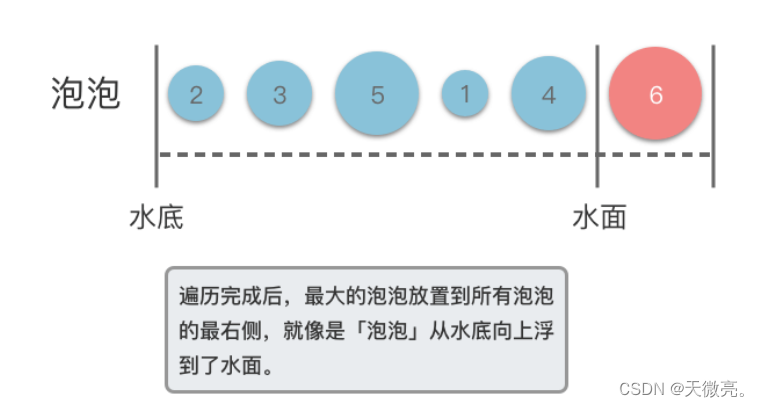
首先将数组想象是一排「泡泡」，元素值的大小与泡泡的大小成正比。
然后从左到右依次比较相邻的两个「泡泡」：
如果左侧泡泡大于右侧泡泡，则交换两个泡泡的位置。
如果左侧泡泡小于等于右侧泡泡，则两个泡泡保持不变。

这趟遍历完成之后，最大的泡泡就会放置到所有泡泡的最右侧，就像是「泡泡」从水底向上浮到了水面。

public class BubbleSort {
    public static void bubbleSort(int[] arr) {
        int len = arr.length;
        for (int i = 0; i < len - 1; i++) {
            boolean flag = true;
            for (int j = 0; j < len - i - 1; j++) {
                if (arr[j] > arr[j + 1]) {
                    int tmp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = tmp;
                    flag = false;
                }
            }
            if (flag) {
                break;
            }
        }
    }
}

选择排序（不稳定）

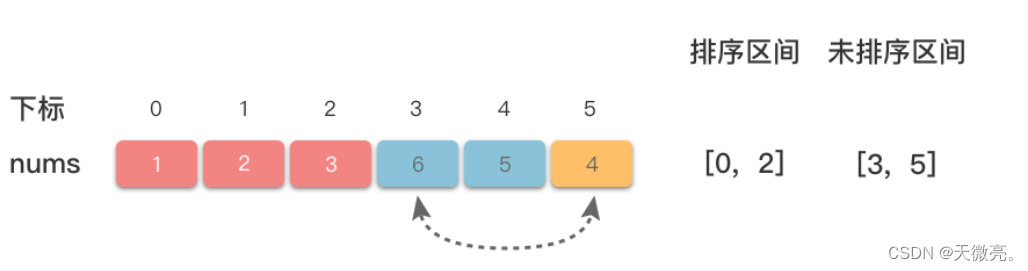
将数组分为两个区间：左侧为已排序区间，右侧为未排序区间。每趟从未排序区间中选择一个值最小的元素，放到已排序区间的末尾，从而将该元素划分到已排序区间。

算法步驟

1. 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置；
2. 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾；
3. 重复第2步，直到所有元素均排序完毕。
   

public class SelectionSort {
    public static void selectionSort(int[] arr) {
        int len = arr.length;
        for (int i = 0; i < len - 1; i++) {
            int minVal = i;
            for (int j = i + 1; j < len; j++) {
                if (arr[minVal] > arr[j]) {
                    minVal = j;
                }
            }
            if (minVal != i) {
                int tmp = arr[i];
                arr[i] = arr[minVal];
                arr[minVal] = tmp;
            }
        }
    }
}

插入排序（稳定）

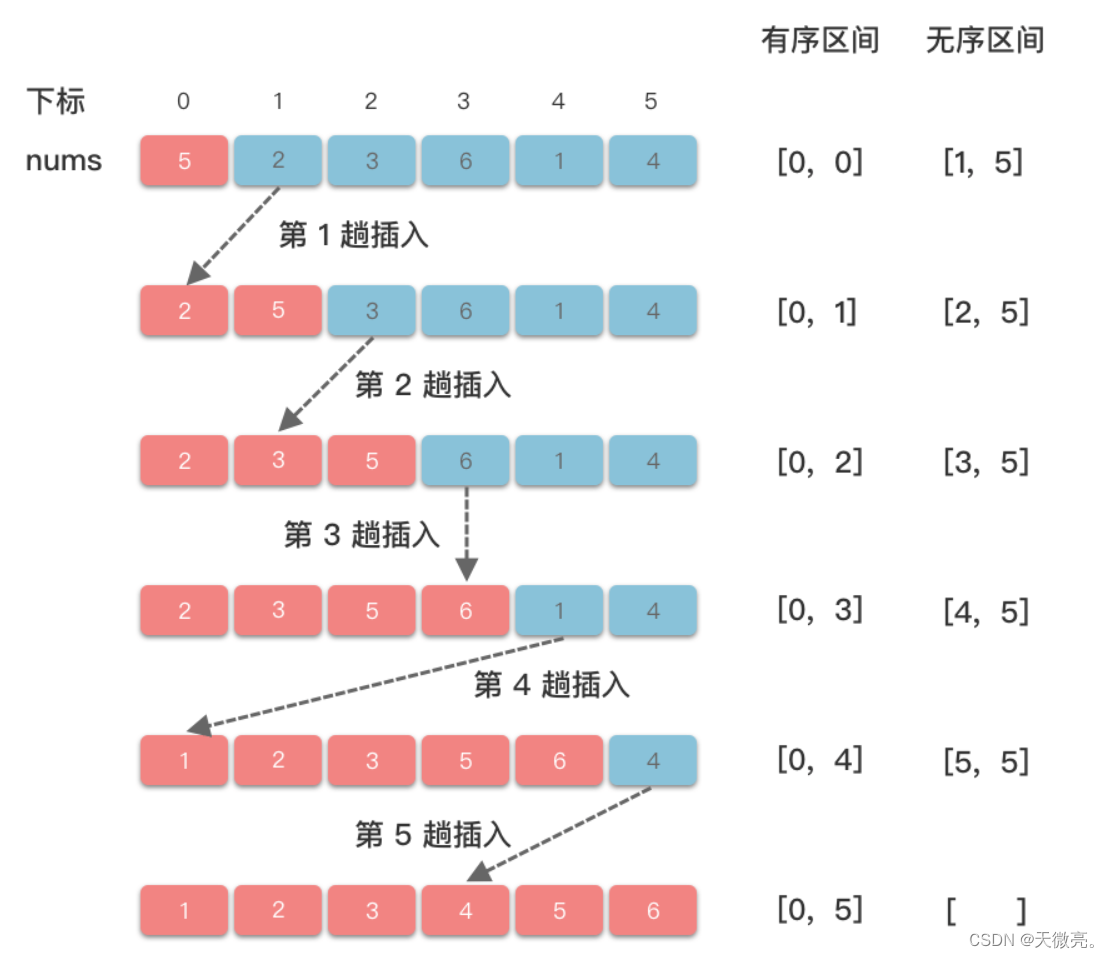
将数组分为两个区间：左侧为有序区间，右侧为无序区间。每趟从无序区间取出一个元素，然后将其插入到有序区间的适当位置。

算法步骤

1. 首先从第一个元素开始，该元素被认为是有序的；
2. 取出下一个元素，在已经排序的元素序列中从后往前进行扫描；
3. 如果该已排好序的元素大于新元素，则将该元素移到下一位置；
4. 重复步骤3一直往前进行扫描比较，直到找到已排序的元素小于或者等于新元素的位置；
5. 将新元素插入到该位置后；
6. 重复步骤2~5。
   

public class InsertionSort {
    public static void insertionSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            int val = arr[i], j = i;
            while (j > 0 && val < arr[j - 1]) {
                arr[j] = arr[j - 1];
                j--;
            }
            arr[j] = val;
        }
    }
}

希尔排序（不稳定）

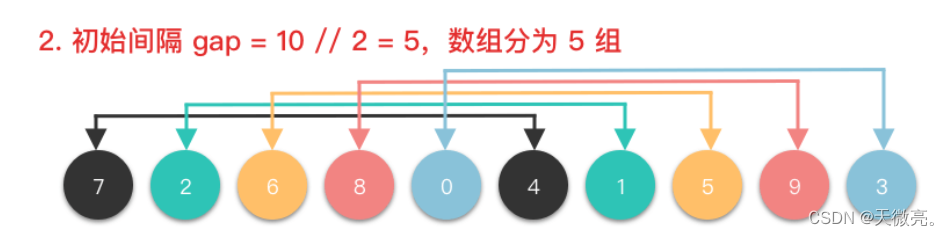
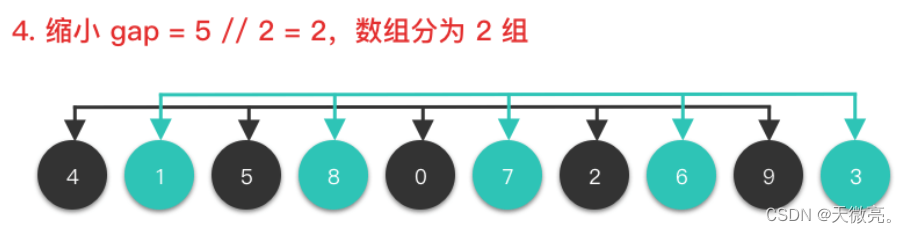
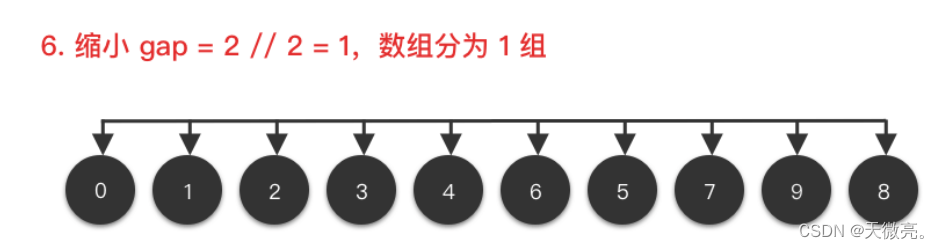
将整个数组切按照一定的间隔取值划分为若干个子数组，每个子数组分别进行插入排序。然后逐渐缩小间隔进行下一轮划分子数组和对子数组进行插入排序。直至最后一轮排序间隔为1，对整个数组进行插入排序。

算法步驟

1. 选择一个增量序列{t1, t2, …, tk}；
2. 按增量序列个数k，对序列进行k趟排序；
3. 每趟排序，根据对应的增量t，将待排序列分割成若干长度为m的子序列，分别对各子表进行直接插入排序。仅增量因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度。
   其中，增量gap=length/2，缩小增量继续以gap = gap/2的方式，这种增量选择我们可以用一个序列来表示，{n/2, (n/2)/2, …, 1}，称为增量序列。一般的增量序列都选择以上说明的这个，但不一定是最优的。

public class ShellSort {
    public static void shellSort(int[] arr) {
        int len = arr.length, tmp, j;
        for (int gap = len / 2; gap >= 1; gap = gap / 2) {
            for (int i = gap; i < len; i++) {
                tmp = arr[i];
                j = i - gap;
                while (j >= 0 && arr[j] > tmp) {
                    arr[j + gap] = arr[j];
                    j -= gap;
                }
                arr[j + gap] = tmp;
            }
        }
    }
}

归并排序（稳定）

采用经典的分治策略，先递归地将当前数组平均分成两半，然后将有序数组两两合并，最终合并成一个有序数组。

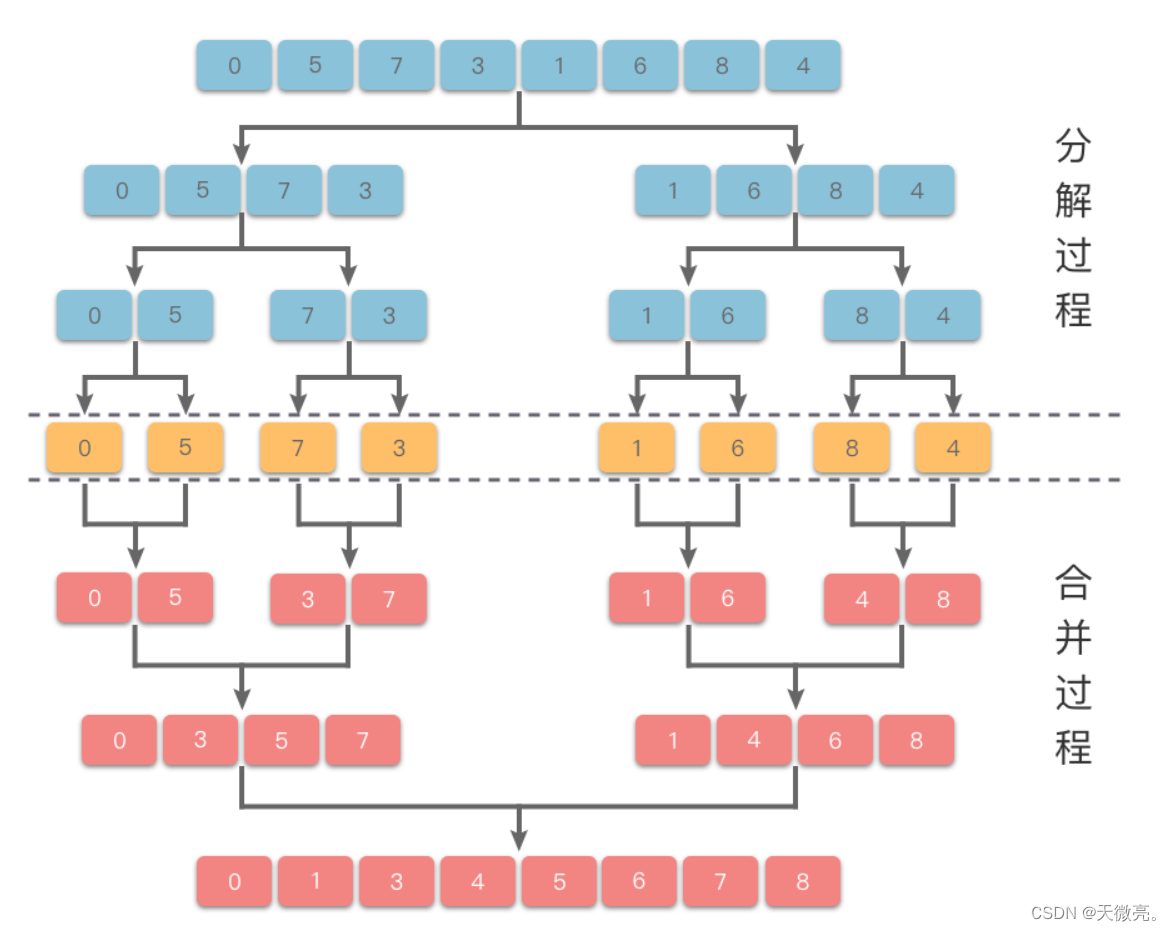
以下是ACWing版本的java模板

public class MergeSort {
 // 归并排序
    private static void merge_sort(int[] arr, int l, int r) {
        // 递归结束条件
        if (l >= r) return;

        // 以下都为逻辑部分
        int mid = l + r >> 1;
        merge_sort(arr, l, mid);
        merge_sort(arr, mid + 1, r);

        int[] tmp = new int[r - l + 1]; // 临时数组, 用于临时存储 [l,r]区间内排好序的数据
        int i = l, j = mid + 1, k = 0;  // 两个指针
        // 进行归并
        while (i <= mid && j <= r) {
            if (arr[i] <= arr[j]) 
                tmp[k++] = arr[i++];
            else
                tmp[k++] = arr[j++];
        }

        while (i <= mid) tmp[k++] = arr[i++];
        while (j <= r) tmp[k++] = arr[j++];

        // 进行赋值
        for (i = l, j = 0; i <= r; i++, j++)
            arr[i] = tmp[j];
    }
}

快速排序（不稳定）

采用经典的分治策略，选择数组中某个元素作为枢轴，通过一趟排序将数组分为独立的两个子数组，一个子数组中所有元素值都比枢轴小，另一个子数组中所有元素值都比枢轴大。然后再按照同样的方式递归的对两个子数组分别进行快速排序，以达到整个数组有序。

以下是ACWing版本的java模板

// 快速排序算法模板（选用）
    public static void quickSort(int[] q,int l,int r){
        if(l>=r)return;
        int i = l-1, j = r+1, x = q[l+r>>1]; //2. 因为j不能取到右边界,所以取下界(q[l]或q[l+r>>1])
        while(i<j){
            do i++; while(q[i]<x);
            do j--; while(q[j]>x);
            if(i<j){
                int tmp = q[i];
                q[i]=q[j];
                q[j]=tmp;
            }
        }
        quickSort(q,l,j);  //1. j不能取到右边界，若取到则会无限递归下去 此时q[j]<=x，q[j+1]>=x而x是2.中定义的
        quickSort(q,j+1,r); 
    }

// 快速排序算法模板（其他）
    public static void quickSort(int[] q,int l,int r){
        if(l>=r)return;
        int i = l-1, j = r+1, x = q[l+r+1>>1]; //2. 因为i不能取到左边界,所以取上界(q[r]或q[l+r+1>>1])
        while(i<j){
            do i++; while(q[i]<x);
            do j--; while(q[j]>x);
            if(i<j){
                int tmp = q[i];
                q[i]=q[j];
                q[j]=tmp;
            }
        }
        quickSort(q,l,i-1);  
        quickSort(q,i,r); //1. i不能取到左边界，若取到则会无限递归下去 此时q[i-1]<=x，q[i]>=x，而x是2.中定义的
    }

堆排序

计数排序

桶排序

基数排序

二分查找

二分查找算法（Binary Search Algorithm）：也叫做折半查找算法、对数查找算法，是一种用于在有序数组中查找特定元素的高效搜索算法。

二分查找的基本算法思想为：通过确定目标元素所在的区间范围，反复将查找范围减半，直到找到元素或找不到该元素为止。

假设所有元素不重复：

public int search(int[] nums, int target) {
        int len = nums.length;
        if (target < nums[0] || target > nums[len - 1]) {
            return -1;
        }
        int left = 0, right = len - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }

整数二分法模板(ACWing版)
二分的本质是边界
二分法用于查找, 每次都选择答案所在的区间再次进行查找, 当区间长度为 1时, 就是答案
可以用来寻找左右边界

// 模板一
//左边界，返回的是第一个>=x的数
// 区间[l, r]被划分成 [l, mid] 和 [mid+1, r]时使用
int bsearch_1(int l, int r) {
    while (l < r) {
        int mid = l + r >> 1;
        //返回的是第一个>=x的数，左边界
        if (q[mid] >= x])  // 可以用check(q[mid]) 判断 mid是否满足性质
            r = mid; 
        else
            l = mid + 1;
    }
    if (q[l] != x) return -1;
    else return l;
}

// 模板二
//右边界，第一个<=x的数
// 区间[l, r]被划分成 [l, mid-1] 和 [mid, r]时使用
int bsearch_2(int l, int r) {
    while (l < r) {
        int mid = l + r + 1 >> 1;   // 注意（+1是为了后面mid-1>=0）
        //右边界
        if (q[mid] <= x)  // check() 判断 mid是否满足性质
            l = mid;
        else
            r = mid - 1;
    }
    if (q[l] != x) return -1;
    else return l;
}
/* 如何选择模板：
根据 check(mid)来判断 r和 l的取值范围
根据取值范围选择 mid是否有 + 1操作
mid归于左边, r = mid, mid选择 不 +1
mid归于右边, l = mid, mid选择 +1 */