图搜索算法 - 深度优先搜索法（DFS）

图搜索算法

图搜索算法也可以叫图的遍历，指从图上任意一个顶点出发，访问图上的所有顶点，而且只能访问一次。这和上一节树的遍历功能类似。但由于图没有层级结构，也没有类似树的根结点那样的特殊顶点，因此相对要复杂一些。本文主要介绍深度优先搜索法（DFS）。

深度优先搜索法（DFS）

根据字面意思，就是顺着起始顶点访问一个没有访问过的顶点，一直走到没有新的顶点可以访问的时候，才往后退回上一个顶点，看一下有没有新的顶点可以访问，如果有又继续深入，直到所有顶点都被访问。这个过程类似浏览网页，点开新闻，再点开体育新闻，然后再看足球新闻，看完今天的足球新闻，那就回到体育新闻，然后访问下一个栏目－篮球新闻。看完了体育新闻，就回到新闻首页，找下一个新闻栏目，如娱乐新闻。

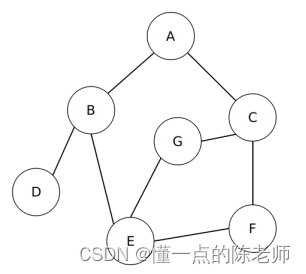
利用深度优先搜索法，从【A】顶点出发来遍历所以结点。然后利用之前学过的栈结构来存储访问记录，下面模拟计算机的访问过程。
（1）首先访问【A】顶点，同时把【A】顶点入栈，如图所示。

（2）顺着【A】顶点，找到未访问的顶点【B】，同时把【B】顶点入栈，如图所示。

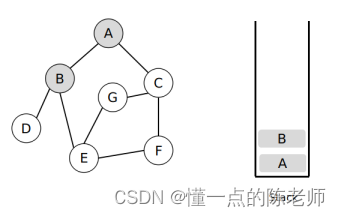
（3）顺着【B】顶点，找到未访问的顶点【D】，同时把【D】顶点入栈，如图所示。

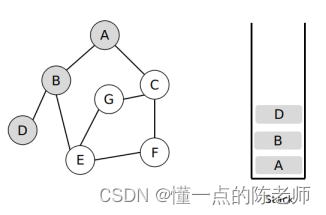
（4）顺着【D】顶点，没有发现未访问的顶点，那么把【D】顶点出栈，然后继续访问栈的头，也就是回到【B】顶点，又发现另外一个未访问的顶点【E】，同时把【E】定入栈，如图所示。

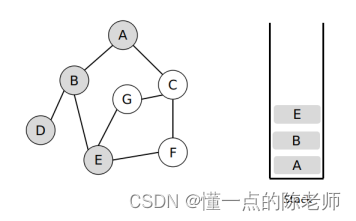
后面的过程也是这样重复下去，最终结果如图所示。

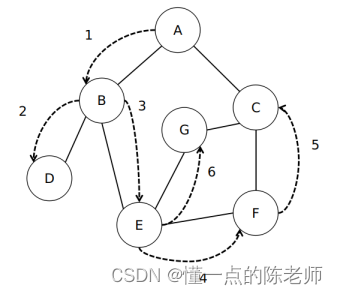
那么现在用代码来表示刚才这个遍历过程。

# 根据图1-43创建无权无向图的邻接列表
graph = {'A': ['B', 'C'],
         'B': ['A', 'D', 'E'],
         'C': ['A', 'F', 'G'],
         'D': ['B'],
         'E': ['B', 'F', 'G'],
         'F': ['C', 'E'],
         'G': ['C', 'E']}
def graph_dfs(adjacency_list, start_point):
    """图的深度优先搜索法"""
    visited = [start_point]      # 保存已经访问过的顶点
    stack = [[start_point, 0]]   # 用栈数据结构来记录访问历史，
    #result = [start_point]
    while stack: # 当栈为空，说明全部顶点已经遍历完成
        (current_point, next_point_index) = stack[-1]  # 获取当前访问的顶点
        if (current_point not in adjacency_list) or (next_point_index >= len(adjacency_list[current_point])):
            stack.pop() # 当前顶点没有新的可以访问关联顶点，那么就出栈
            continue
        next_point = adjacency_list[current_point][next_point_index]
        stack[-1][1] += 1            # 记录当前访问的顶点的这个关联顶点已经被访问
        if next_point in visited:    # 若已经访问了，继续找下一个
            continue
        visited.append(next_point)   # 若是新的顶点，那就添加到已访问顶点
        stack.append([next_point, 0])# 新的顶点入栈　
    return visited  # 返回访问顶点的结果
#------------测试--------------------
res = graph_dfs(graph, 'A')
print("->".join(res))
#------------结果--------------------
A->B->D->E->F->C->G
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30