c++ set 容器详解 附例题题解

声明

本文中题解部分内容一部分转载自 @sonnety 的这篇博客中，本文为为方便复习而写的结论类文章，读者可自行跳转至原文处阅读。

---

PART 1 set

什么是 set

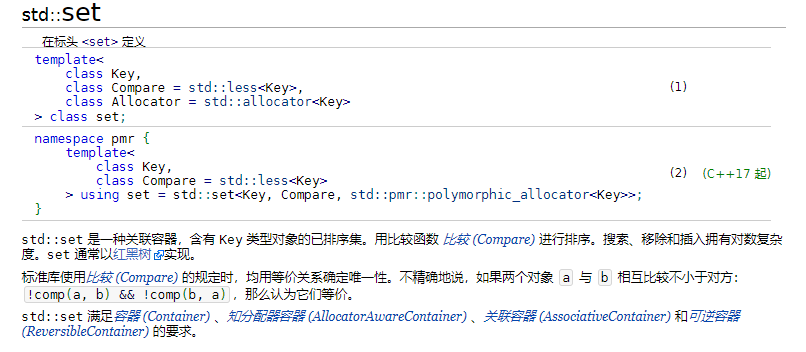
——来源cppreference

简言之，它就是一种存进去就可以自动按升序排列的特殊容器，通常的 set 还具有自动去重的功能。

定义方式：

std::set<int>s;
'set'+<存储数据类型>+容器名

注意的是，这里存储数据类型不仅包含常用的int，long long，double等易想到的，也可以是char，string这些非数值类的，排序标准为字典序（强者处处是惊喜）。

怎么使用 set

首先，我们要了解几个 set 的常用方法：

指针类
s.begin()//返回 s 的起始迭代器
s.end()//返回 s 的超尾迭代器
/*
update：通用性更高的两个推荐函数
s.begin()——>std::begin(s)
s.end()——>std::end(s)
*/
容量类
s.empty()//检查容器是否为空
s.size()//返回元素数（返回值类型为 std::size_t 通常情况下是 unsigned long long ）
修改类
s.insert(w)//向容器中插入 w 这个元素
s.erase(w)//在容器中删除 w 这个元素
          //参数为迭代器，并返回新的迭代器
s.clear()//将 s 清空
swap(s1,s2)//交换 s1 与 s2 两个容器内的元素
查找类
s.find(w)//在容器中查找 w 这个元素所在的迭代器
         //若不存在该元素，则返回 s.end()
s.lower_bound(w)//在容器中寻找第一个不小于 w 的元素迭代器
                //若不存在则返回 s.end()

我们可以观察到，很多 set 的返回值类型都是迭代器，因此还存在一个迭代器set::iterator，它是一个指向 set 中元素的仿指针，可以通过迭代器访问 set 中的元素，并能够进行迭代器运算，如自增等操作。

注：迭代器的功能比指针多得多，并且安全性也更高。

我们在调用 s 中的值的时候，可以如下操作：

输出 s 中的所有值
set<int>::iterator it;
for(it=s.begin();it!=s.end();it++)
    cout<<*it<<' ';// *it 是获取当前迭代器指向的元素的值

自 c++11 引入了类型 auto 以及 range-for 语法后，我们可以更加简便地完成上面的操作。

for(auto it:s)
	cout<' ';//这里 auto 的类型等同于我们定义 s 时的数据类型，也就是 int 
所以它等同于：
for(int it:s)
	cout<' ';

set 和 multiset

multiset 在 cppreference 中定义如下：

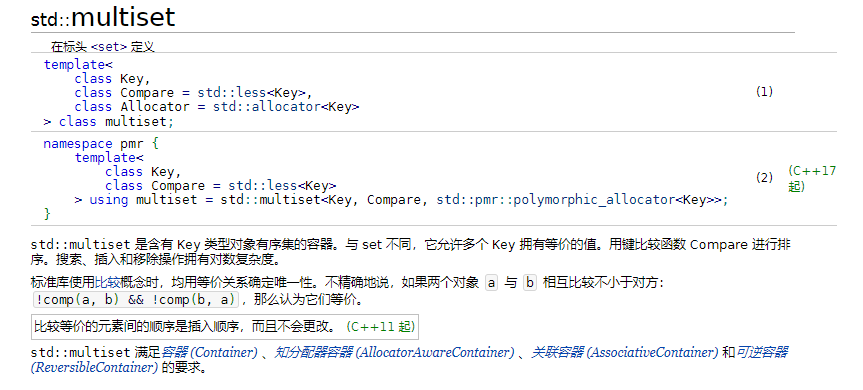
简言之， multiset 的特性有：

1. 可以保留重复的元素，也就是没有自动去重的性质。
2. multiset 支持插入、删除和查找操作的平均时间复杂度均为 $O(logn)$，而 set 只支持插入和查找操作的平均时间复杂度为 $O(logn)$，删除操作的平均时间复杂度为 $O(1)$。
3. multiset 在删除时只会删除元素值相同的元素中的一个，而不是全部删除或删除一些。

通常情况下，我们多使用 set ，因为它在进行查找等操作时更快；而只有在需要保留重复元素的少数情况下，我们使用 multiset ，下题就是一个例子。

一些其他性质

由于这位不小心故意把代码打错了，于是有了这一框，后续发现奇特的性质也会添加。

错误代码部分：

if(s[1][2])
	swap(s[1],s[2]);

意外地发现题目能过，初步猜测对两个 set 比较返回的是 $size$ 之间的比较。

但经过一定的探讨后发现，这里比较的是两个容器队首元素的字典序（神奇）！

探究过程

假说演绎法？

s[1].insert(99);
s[1].insert(2);
s[2].insert(3);
s[2].insert(55);
s[2].insert(66);
if(s[1]2])
	cout<<"1";
else
	cout<<"2";

如果排序准则为 size ，那么这里有 $s[i].size()=2$，$s[2].size()=3$，应该输出2，但结果输出的是1；

我们将代码第二行改为 s[1].insert(4) 后，输出结果变成了2；

于是我们发现，这里的比较与 $s.size()$ 无关，而与队首元素值有关，经过一些资料的搜寻，我们得到结论：

将两个 set 容器进行比较，实质为比较两个容器队首元素的字典序。

PART 2 大根堆

题面

题库

思路

常规办法为线段树合并，但太长了不想写 但总感觉有更优的做法，所以就有了下面基于 set 优化的启发式合并做法。

我们可以通过 dp 引入，固定一点作为根结点，用f[u][i]表示以 $u$ 为树根的子树里结点权值小于 $i$ 的个数，其中 $i\le v_u$；用 $siz{e}_u$ 表示以 $u$ 为根的树的大小。

那么很容易能想到状态转移方程为：

$$f[u][i]=\sum _{siz{e}_u}f[u][i]，i\le v_u$$

$$f[u][i]=max(\sum _{siz{e}_u}f[u][i],\sum _{siz{e}_u}f[u][i+1]-1),i\ge v_u$$

那么如何存储？ multiset ！

set 自带的查找功能可以很方便的判断条件是否成立， $size$ 函数也直接提供了上述 $size$ 数组。

使用 dfs 进行遍历，由子结点逐个回溯至根节点，最后根节点的 $size$ ，即为答案。

代码中加入了部分注释，供参考。

code:

#include
inline int qr()
{
	char ch=getchar();int x=0,f=1;
	for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;
	for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<3)+(x<<1)+(ch^48);
	return x*f;
}
#define qr qr()
using namespace std;
const int Ratio=0;
const int N=500005;
int n,cnt;
int va[N],hh[N],to[N],ne[N];
multiset<int>f[N];
namespace Wisadel
{
	void Wadd(int u,int v)
	{//加边 
		to[++cnt]=v;
		ne[cnt]=hh[u];
		hh[u]=cnt;
	}
	void Wdfs(int u,int fa)
	{
		for(int i=hh[u];i!=-1;i=ne[i])
		{//遍历 
			int t=to[i];
			if(t==fa)
				continue;
			Wdfs(t,u);
			if(f[u].size()size())
				swap(f[u],f[t]);
			//堆，所以父节点的大小应大于子节点 
			for(auto j:f[t])
				f[u].insert(j);
			//合并
			f[t].clear();
			//擦去被合并了的树
		}
		if(f[u].size()>0&&f[u].lower_bound(va[u])!=f[u].end())
			f[u].erase(f[u].lower_bound(va[u]));
		//因为是大根堆，所以子应小于父
		//那么若存在比父大的元素，这个堆便不成立
		//擦去它 
		f[u].insert(va[u]);
		//把当前结点（根节点）插入 
	}
	short main()
	{
		memset(hh,-1,sizeof hh);
		n=qr;
		for(int i=1;i<=n;i++)
		{
			va[i]=qr;int b=qr;
			if(i!=1)
				Wadd(i,b),Wadd(b,i);
		}
		Wdfs(1,-1);
		printf("%d\n",(int)f[1].size());
		//我们所用dfs的遍历形式，保证了会先将尽头的子树遍历尽
		//所以每个结点遍历后的结果，是包含了它以及它子树的最优解
		//所以经过交换，最后答案会体现在f[1]容器内元素的个数 
		return Ratio;
	}
}
int main(){return Wisadel::main();}

PART 3 领导集团问题

题面

洛谷 题库

思路

与上题大根堆思路基本一致，这道题要求形成小根堆，只需加一点修改即可。

1. 输入是分步输入，连边时改成了 $v_i$ 与 $i+1$ 连边（不会有人注意不到吧 除了我）；
2. 由于小根堆子大于父，应擦去比父小的元素，也就是判断时改为与 f.begin() 进行比较；
3. 删除元素时，由于 lower_bound 返回的是第一个不小于的值，应删除的是找到的元素的上一个，需要用到上面提到过的 iterator 迭代器，详见代码。

另外，这道题的数据范围明显增大，由于用到了 set 容器，不能随心所欲一次开最大（悲，所以要稍微缩小一点。

code:

为防止篇幅过长，我仅保留了主要的代码部分。

const int N=2000005;
int n,cnt;
int va[N],hh[N<<1],to[N<<1],ne[N<<1];
multiset<int>f[N];
namespace Wisadel
{
	void Wadd(int u,int v)
	{//加边 
		to[++cnt]=v;
		ne[cnt]=hh[u];
		hh[u]=cnt;
	}
	void Wdfs(int u,int fa)
	{
		for(int i=hh[u];i!=-1;i=ne[i])
		{//遍历 
			int t=to[i];
			if(t==fa)
				continue;
			Wdfs(t,u);
			if(f[u].size()size())
				swap(f[u],f[t]);
			for(auto j:f[t])
				f[u].insert(j);
			f[t].clear();
		}
		multiset<int>::iterator it=f[u].lower_bound(va[u]); 
		//使用iterator迭代器先找到 lower_bound(va[u]) 的位置 
		if(f[u].size()>0&&it!=f[u].begin())
			f[u].erase(--it);
		//这个迭代器可以进行自增，自减等运算，很方便 
		f[u].insert(va[u]);
	}
	short main()
	{
		memset(hh,-1,sizeof hh);
		n=qr;
		fo(i,1,n)
			va[i]=qr;
		fo(i,2,n)
		{
			int a=qr;
			Wadd(i,a),Wadd(a,i);
		}
		Wdfs(1,-1);
		printf("%d\n",(int)f[1].size());
		return Ratio;
	}
}
int main(){return Wisadel::main();}

---

完结撒花~