【数据结构】二叉树（定义、性质、存储、遍历、构造）解析+完整代码

1.树的基本概念

• 定义

  

  • 空树：结点数为0的树
  • 非空树：有且仅有一个根结点
  • 叶子结点：没有后继的结点（终端结点）
  • 分支节点：有后继的结点（非终端结点）
  • 根节点没有前驱，其他任何一个结点都有且仅有一个前驱

• 基本术语

  • 1.度

    结点的度：树中一个结点的孩子个数。

    树的度：树中结点的最大度数。

  • 2.结点的深度（层次）

    从上往下数，在第几层。

  • 3.结点的高度

    从下往上数，在第几层。

  • 4.树的高度（深度）

    总共多少层。

  • 5.有序树和无序树

    有序树：树中各子树从左至右是有次序的，不能互换。

    无序树：子树无次序，可以互换。

  • 6.森林

    森林是m棵互不相交的树的集合

• 树的性质

  • 1.结点数=总度数+1

    度数即孩子的个数，加一的那个为根结点

  • 2.度为m的树、m叉树的区别

    

  • 3.度为m的树第i层至多有$m^{i-1}$个结点

    ​ m叉树第i层至多有$m^{i-1}$个结点

    

  • 4.高度为h的m叉树至多有$\frac{m^h-1}{m-1}$个结点

    

  • 5.高度为h的m叉树至少有h个结点

    高度为h、度为m的树至少有h+m-1个结点

    

  • 6.具有n个结点的m叉树的最小高度为$\lceil lo{g}_m(n(m-1)+1)\rceil$

    根据不等式求解：

    

2.二叉树的概念

2.1 二叉树定义和特性

• 定义

  1.每个结点至多有两棵子树；

  2.左右子树不能颠倒（二叉树是有序树）。

• 特殊二叉树

  • 1.满二叉树

    一棵高度为h，且含有$2^h-1$个结点的二叉树。

    特点：

    （1）只有最后一层有叶子结点；

    （2）不存在度为1的结点；

    （3）按层序从1开始编号，结点i的左孩子为$2i$，右孩子为$2i+1$；结点i的父节点为$\lfloor i/2\rfloor$。

    

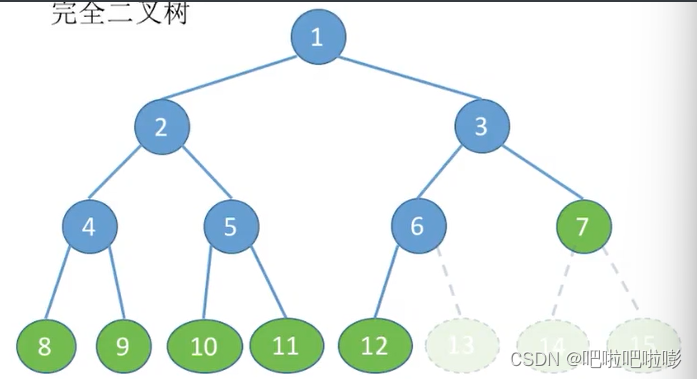
  • 2.完全二叉树

    当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时，称为完全二叉树。

    即 在满二叉树的基础上，最后一层可以不满。

    特点：

    （1）只有最后两层可能有叶子结点；

    （2）最多只有一个度为1的结点；

    （3）和满二叉树相同：按层序从1开始编号，结点i的左孩子为$2i$，右孩子为$2i+1$；结点i的父节点为$\lfloor i/2\rfloor$。

    （4）$i<\lfloor n/2\rfloor$为分支结点，$i>\lfloor n/2\rfloor$为叶子结点。

    （5）如果一个结点只有一个孩子，那一定是左孩子不是右孩子。

    

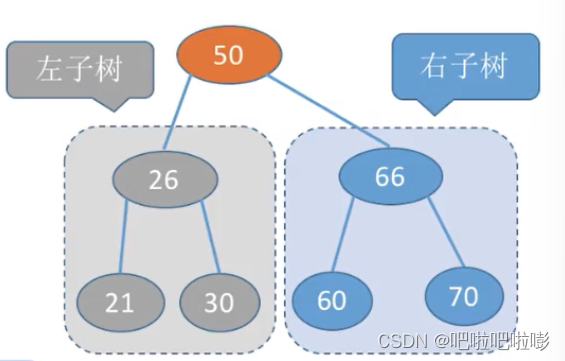
  • 3.二叉排列树

    若一棵二叉树满足：左子树的元素<根节点<右子树

    

  • 4.平衡二叉树

    树上任一结点的左子树和右子树的深度之差不超过1。

    

2.2 二叉树性质

• 1.设非空二叉树中度为0，1，2的结点个数分别为$n_0、n_1、n_2$，则$n_0=n_2+1$。（叶子结点比二分支结点多一个）

  推导：

• 2.二叉树第i层至多有$2^{i-1}$个结点

  ​ （m叉树第i层至多有$m^{i-1}$个结点）

  

• 3.高度为h的二叉树至多有$2^h-1$个结点（满二叉树）

  

• 4.对于完全二叉树，具有n个结点的完全二叉树的高度h为$\lceil lo{g}_2(n+1)\rceil$或$\lfloor lo{g}_{2}n\rfloor +1$

  推导：
  

• 5.对于完全二叉树，可以由结点数n推出度为0，1，2的结点个数为$n_0、n_1、n_2$，完全二叉树最多只有一个度为1的结点，即

  $n_1=0或1$

  $n_0=n_2+1$ —> $n_0+n_2$一定是奇数

  ====》

  若完全二叉树有2k个（偶数）个结点，则必有 $n_1=1,n_0=k,n_2=k-1$

  若完全二叉树有2k-1个（奇数）个结点，则必有$n_1=0,n_0=k,n_2=k-1$

2.3 二叉树的存储

2.3.1 顺序存储

• 结构体

  struct TreeNode{
      ElemType value; //结点中的数据元素
      bool isEmpty; //结点是否为空
  };
  1
  2
  3
  4

• 用数组定义，按从上至下（一层层）、从左至右的顺序依次存储完全二叉树中各个结点

  TreeNode t[MaxSize];
  1

• 初始化时标记所有结点为空

  for(int i=0;i<MaxSize;i++){
      t[i].isEmpty=true;
  }
  1
  2
  3

  

• 完全二叉树 顺序存储后的几个基本操作

  • i的左孩子 —— $2i$
  • i的右孩子 —— $2i+1$
  • i的父节点 —— $\lfloor i/2\rfloor$
  • i所在层次 —— $\lceil lo{g}_2(n+1)\rceil$或$\lfloor lo{g}_{2}n\rfloor +1$

• 若完全二叉树中共有n个结点，则

  • 判断i是否有左孩子？

    $2i<=n$

  • 判断i是否有右孩子？

    $2i+1<=n$

  • 判断i是否是叶子/分支结点？

    $i>\lfloor n/2\rfloor$

• 非完全二叉树中，，把二叉树的结点编号与完全二叉树的对应起来：

  

  • 这种存储方式会浪费很多空间。

  • 最坏情况：高度为h且只有h个结点的单支树（所有结点只有右孩子），也至少需要$2^h-1$个存储单元。

  ∴ 二叉树的顺序存储只适合存储完全二叉树。

2.3.2 链式存储

• 结构体

  typedef struct BiTNode{
      ElemType data;
      struct BiTNode *lchild,*rchild; //每个结点都有左右两个孩子的指针
      struct BiTNode *parent; //可不加父指针
  }BiTNode,*BiTree;
  1
  2
  3
  4
  5

• 注：n个结点的二叉链表共有n+1个空链域：

  

3.二叉树的遍历

• 遍历：按照某种次序把所有结点都访问一次。

• 分类

  先序遍历：根左右（NLR）

  中序遍历：左根右（LNR）

  后序遍历：左右根（LRN）

  

• 手算方法：分支节点逐层展开法

  

• 复杂度

  • 时间复杂度：

    ∵ 每个结点都访问一次且只访问一次，

    ∴ 时间复杂度$O(n)$。

  • 空间复杂度：

    ∵ 最坏情况下，二叉树是有n个结点且深度为n的单支树，计算机中递归实现用栈存储，

    ∴ 空间复杂度为$O(n)$。

3.1 先序遍历

• 先序遍历过程：根左右（NLR）

  1.若二叉树为空，什么都不做；

  2.若二叉树非空：

  ​ （1）访问根结点；

  ​ （2）先序遍历左子树；

  ​ （3）先序遍历右子树。

typedef struct BiTNode{
    ElemType data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

void PreOrder(BiTree T){
    if(T!=NULL){
        visit(T); //访问根结点
        PreOder(T->lchild); //递归遍历左子树
        PreOrder(T->rchild); //递归遍历右子树
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

3.2 中序遍历

• 中序遍历过程：左根右（LNR）

  1.若二叉树为空，什么都不做；

  2.若二叉树非空：

  ​ （1）先序遍历左子树；

  ​ （2）访问根结点；

  ​ （3）先序遍历右子树。

typedef struct BiTNode{
    ElemType data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

void InOrder(BiTree T){
    if(T!=NULL){
        PreOder(T->lchild); //递归遍历左子树
        visit(T); //访问根结点
        PreOrder(T->rchild); //递归遍历右子树
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

3.3 后序遍历

• 后序遍历过程：左右根（LRN）

  1.若二叉树为空，什么都不做；

  2.若二叉树非空：

  ​ （1）先序遍历左子树；

  ​ （2）先序遍历右子树。

  ​ （3）访问根结点。

typedef struct BiTNode{
    ElemType data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

void PostOrder(BiTree T){
    if(T!=NULL){
        PreOder(T->lchild); //递归遍历左子树
        PreOrder(T->rchild); //递归遍历右子树
        visit(T); //访问根结点
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

3.4 层序遍历

• 算法思想

  • 层序遍历 就是从上往下一层一层访问

  1.初始化一个辅助队列；

  2.根结点入队；

  3.若队列非空，则队头结点出队，访问该节点，并将其左右孩子插入队尾；

  4.重复第三次直到队列空。

void LevelOrder(BiTree T){
    LinkQueue Q;
    InitQueue(Q);
    BiTree p;
    EnQueue(Q,T); //将根结点入队
    while(!IsEmpty(Q)){ //队列不空则循环
        DeQueue(Q,p); //队头结点出队
        visit(p); //访问出队结点
        if(p->lchild!=NULL)
            EnQueue(Q,p->lchild); //左孩子入队
        if(p->rchild!=NULL)
            EnQueue(Q,p->rchild); //右孩子入队
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

• 补充代码：链式队列结点

  typedef struct LinkNode{
      BiTNode *data;
      struct LinkNode *next;
  }LinkNode;
  
  typedef struct{
      LinkNode *front,*rear; //队头队尾指针
  }LinkQueue;
  1
  2
  3
  4
  5
  6
  7
  8

3.5 由遍历序列构造二叉树

• 若只给出一棵二叉树的 前中后层 序遍历中的一种，不能唯一确定一棵二叉树。

  • 构造的三种方法：
    1. 前序+中序
    2. 后序＋中序
    3. 层序+中序

A.前序+中序遍历序列

• 步骤

  1.找到根结点：先序序列第一个结点==根节点；

  2.在中序序列中找到根结点，根据根结点把序列分成：左子树+根结点+右子树；

  3.左右子树分别重复第1、2步。

• 方法：根据根结点推，前序遍历序列的第一个就是根节点。

  

B.后序+中序遍历序列

• 方法：根据根结点推，后序遍历序列的最后一个一个就是根结点。

  

C.层序+中序遍历序列

• 方法：

  

*完整代码 二叉树

#include 
#include 
#include 

#define ElemType int

// 二叉树链式存储结构
typedef struct BiTNode {
    ElemType data; // 数据域
    struct BiTNode *lchild, *rchild; // 左右孩子指针
} BiTNode, *BiTree;

// 访问结点
void visit(BiTNode *Node) {
    printf("%d ", Node->data);
}

// 先序遍历：根左右
void PreOrder(BiTree T) {
    if (T != NULL) {
        visit(T); // 访问根结点
        PreOrder(T->lchild);
        PreOrder(T->rchild);
    }
}

// 中序遍历：左根右
void InOrder(BiTree T) {
    if (T != NULL) {
        InOrder(T->lchild);
        visit(T);
        InOrder(T->rchild);
    }
}

// 后序遍历：左右根
void PostOrder(BiTree T) {
    if (T != NULL) {
        PostOrder(T->lchild);
        PostOrder(T->rchild);
        visit(T);
    }
}

// 层序遍历：借助队列
// 链式队列结点
typedef struct LinkNode {
    BiTNode *data;
    struct LinkNode *next;
} LinkNode;

typedef struct {
    LinkNode *front, *rear;
} LinkQueue;

void InitQueue(LinkQueue *Q) {
    Q->front = Q->rear = (LinkNode *)malloc(sizeof(LinkNode));
    Q->front->next = NULL; // 将头节点的 next 指针初始化为 NULL
}

void Push(LinkQueue *Q, BiTNode *x) {
    LinkNode *p = (LinkNode *)malloc(sizeof(LinkNode));
    p->data = x;
    p->next = NULL;
    Q->rear->next = p;
    Q->rear = p;
}

void Pop(LinkQueue *Q, BiTNode **x) {
    LinkNode *p = Q->front->next;
    *x = p->data;
    Q->front->next = p->next;
    if (Q->rear == p) Q->rear = Q->front;
    free(p);
}

bool Empty(LinkQueue *Q) { // 修改函数参数
    if (Q->rear == Q->front)
        return true;
    else
        return false;
}

void LevelOrder(BiTree T) {
    LinkQueue Q;
    InitQueue(&Q);
    BiTree p;
    Push(&Q, T); // 根结点入队
    while (!Empty(&Q)) {
        Pop(&Q, &p); // 队头结点出队
        visit(p);
        // 若左孩子不为空，则入队
        if (p->lchild != NULL) {
            Push(&Q, p->lchild);
        }
        // 若右孩子不为空，则入队
        if (p->rchild != NULL) {
            Push(&Q, p->rchild);
        }
    }
}

// 中序加先序遍历构造二叉树
BiTree InPreCreateBiTree(ElemType in[], ElemType pre[], int inStart, int inEnd, int preStart, int preEnd) {
    if (inStart > inEnd || preStart > preEnd) return NULL;
    BiTree root = (BiTNode *)malloc(sizeof(BiTNode));
    root->data = pre[preStart]; // 根节点为先序遍历的第一个节点
    int rootIndex;
    for (rootIndex = inStart; rootIndex <= inEnd; rootIndex++) {
        if (in[rootIndex] == pre[preStart]) // 在中序遍历中找到根节点位置
            break;
    }
    int leftLength = rootIndex - inStart; // 左子树长度
    root->lchild = InPreCreateBiTree(in, pre, inStart, rootIndex - 1, preStart + 1, preStart + leftLength); // 递归构造左子树
    root->rchild = InPreCreateBiTree(in, pre, rootIndex + 1, inEnd, preStart + leftLength + 1, preEnd); // 递归构造右子树
    return root;
}

// 中序加后序遍历构造二叉树
BiTree InPostCreateBiTree(ElemType in[], ElemType post[], int inStart, int inEnd, int postStart, int postEnd) {
    if (inStart > inEnd || postStart > postEnd) return NULL;
    BiTree root = (BiTNode *)malloc(sizeof(BiTNode));
    root->data = post[postEnd]; // 根节点为后序遍历的最后一个节点
    int rootIndex;
    for (rootIndex = inStart; rootIndex <= inEnd; rootIndex++) {
        if (in[rootIndex] == post[postEnd]) // 在中序遍历中找到根节点位置
            break;
    }
    int leftLength = rootIndex - inStart; // 左子树长度
    root->lchild = InPostCreateBiTree(in, post, inStart, rootIndex - 1, postStart, postStart + leftLength - 1); // 递归构造左子树
    root->rchild = InPostCreateBiTree(in, post, rootIndex + 1, inEnd, postStart + leftLength, postEnd - 1); // 递归构造右子树
    return root;
}

int main() {
    ElemType in[] = {4, 7, 2, 1, 5, 3, 8, 6}; // 中序序列
    ElemType pre[] = {1, 2, 4, 7, 3, 5, 6, 8}; // 先序序列
    ElemType post[] = {7, 4, 2, 5, 8, 6, 3, 1}; // 后序序列
    ElemType level[] = {1, 2, 3, 4, 5, 6, 7, 8}; // 层序序列

    BiTree rootInPre = InPreCreateBiTree(in, pre, 0, 7, 0, 7);
    BiTree rootInPost = InPostCreateBiTree(in, post, 0, 7, 0, 7);
    // 中序加层序构造二叉树需要给定中序和层序序列，由于层序序列不是标准的输入序列，无法直接用现有函数构造，暂不实现

    printf("InPreOrder: ");
    PreOrder(rootInPre);
    printf("\n");

    printf("InOrder: ");
    InOrder(rootInPre);
    printf("\n");

    printf("InPostOrder: ");
    PostOrder(rootInPost);
    printf("\n");

    printf("LevelOrder: ");
    LevelOrder(rootInPre);
    printf("\n");

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162