动态规划——斐波那契数列模型：面试题08.01.三步问题

题目描述

题目链接：面试题08.01.三步问题

如果n是0走法可能是1也可能是0，所以本题范围并不需要考虑直接从1开始即可

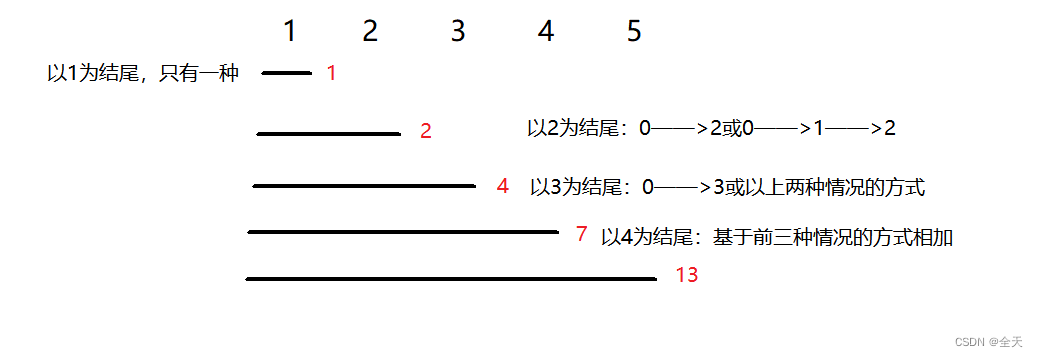
因为以3为结尾有直接从0到3的方式，其他的方式则需要经过前面的阶梯，所以则是基于前面的方式来计算当前位置的方式，以此类推。
PS：答案可能过大，所以题目要求需要取模1e9 + 7。

算法原理

1.状态表示

经验+题目要求：经验一般是以…开始，以…结尾。
dp[i]:表示到达i位置时，一共有多少种方式。

2.状态转移方程

dp[i] = dp[i -1] + dp[i - 2] + dp[i - 3]

3.初始化

dp[1] = 1,dp[2] = 2,dp[3] = 4

4.填表顺序

从左往右

5.返回值

dp[n]

代码实现

C++

class Solution {
public:
    int waysToStep(int n) {
        //单独处理边界条件
        if(n < 3)return n;
        else if(n == 3)return 4;
        //1.创建dp表
        vector<int> dp(n + 1);
        const int MOD = 1e9 + 7;
        //2.初始化
        dp[1] = 1,dp[2] = 2,dp[3] = 4;
        //3.填表
        for(int i = 4;i <= n;++i){
        	//处理溢出问题
            dp[i] = ((dp[i - 3] + dp[i - 2]) % MOD + dp[i - 1]) % MOD;
        }
        //4.返回值
        return dp[n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Java

class Solution {
    public int waysToStep(int n) {
        // 1. 创建 dp 表
        // 2. 初始化
        // 3. 填表
        // 4.返回值
        int MOD = (int) 1e9 + 7;

        // 处理⼀下边界情况
        if (n == 1 || n == 2)
            return n;
        if (n == 3)
            return 4;

        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 4;
        for (int i = 4; i <= n; i++)
        	//处理溢出问题
            dp[i] = ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;
        return dp[n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24