GAN 生成对抗神经网络

GAN

GAN的结构

GAN的设计灵感来源于博弈论中的零和博弈（Zero-sum Game），在零和博弈中，参与双方的收益是完全相反的，一方的收益必然导致另一 方的损失，总收益为零。

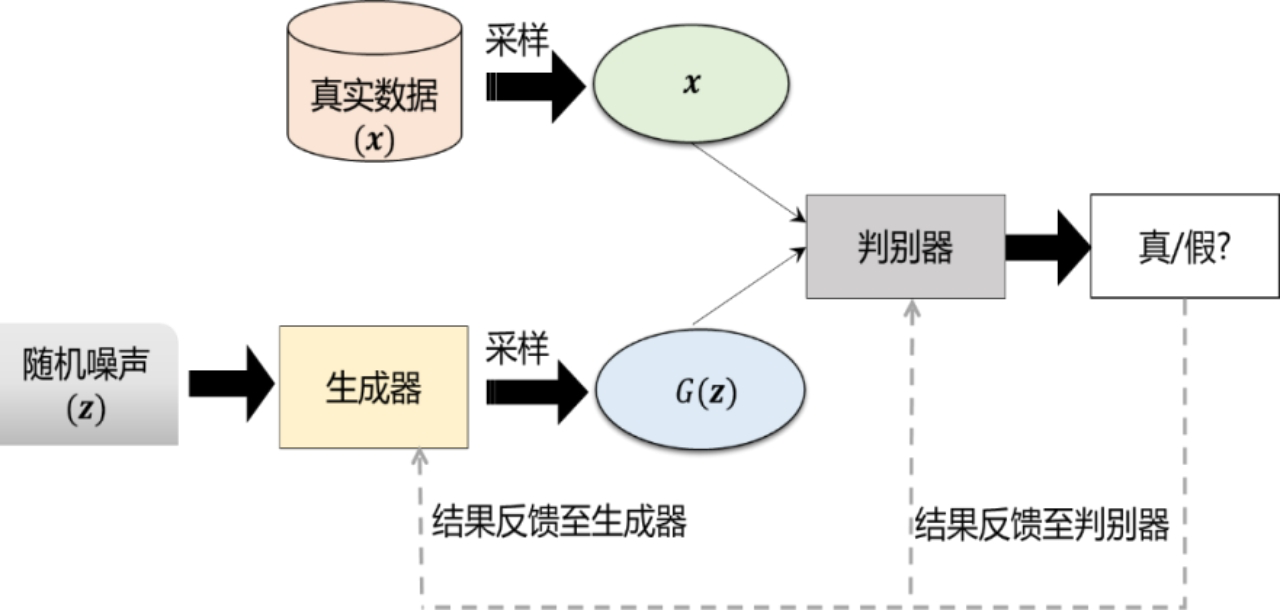
GAN 主 要 由 两 部 分 组 成 ： 生 成 器 （ Generator ） 和 判 别 器 （Discriminator），它们分别扮演了两个不同的角色。 生成器的任务是生成接近真实数据分布的样本，而判别器的任务则是尽可 能地区分真实的样本和生成器生成的样本。 通过生成器和判别器之间的对抗，GAN可以学习到生成高质量样本的能力。

以图片生成为例： 生成器是一个生成图片的网络，它使用服从某一分布（均匀分布或高斯 分布）的噪声生成一个类似真实训练数据的图片，记作𝐺(𝒛)，追求效果 是越像真实图片越好。 判别器是一个二分类器，用来判断一个图片是不是“真实的” ，它的输入是采样的真实图片𝒙以及生成器生成的图片𝐺(𝒛)，输出是输入图片是真实图片的概率，如果输入图片来自真实数据，那么判别器输出大的概率，否则，输出小的概率。

GAN的目标函数

GAN的目标是使生成器生成的数据能够骗过判别器，因此需要定义一个目标函数，使得判别器判断真实样本为“真” 、生成样本为“假”的概率最小化。
$$\underset{G}{\min }\underset{D}{\max }V(D,G)=E_{\mathbf{x}\sim p_{data}(\mathbf{x})}[logD(\mathbf{x})]+E_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}[\log (1-D(G(\mathbf{z})))]$$
其中，$V(D,G)$表示真实样本和生成样本的差异程度；$p_{data}(x)$表示真实数据$x$的分布，$p_z(z)$表示噪声z的分布，$D(x)$表示判别器认为$x$是真实样本的概率，$D(G(\mathbf{z}))$表示判别器认为生成样本$G(\mathbf{z})$是假的概率。

训练GAN的时候，判别器希望目标函数最大化，也就是使判别器判断真实样本为“真” 、判断生成样本为“假”的概率最大化，要尽量最大化自己的判别准确率。可以写作损失函数的形式：
$$L(G,D)=-E_{x\sim p_{data}(x)}[\log D(x)]-E_{z\sim p_z(z)}[\log (1-D(G(z)))]$$
与判别器相反，生成器希望目标函数最小化，也就是迷惑判别器，降低其对数据来源判断正确的概率，也就是最小化判别器的判别准确率。如果采用零和博弈，生成器的目标是最小化𝑉(𝐷, 𝐺)，而实际操作时发现零和博弈的训练效果并不好，生成模型一般采用最小化公式：
$$E_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}[\log \left(1-D(G(\mathbf{z}))\right)]$$

GAN的训练

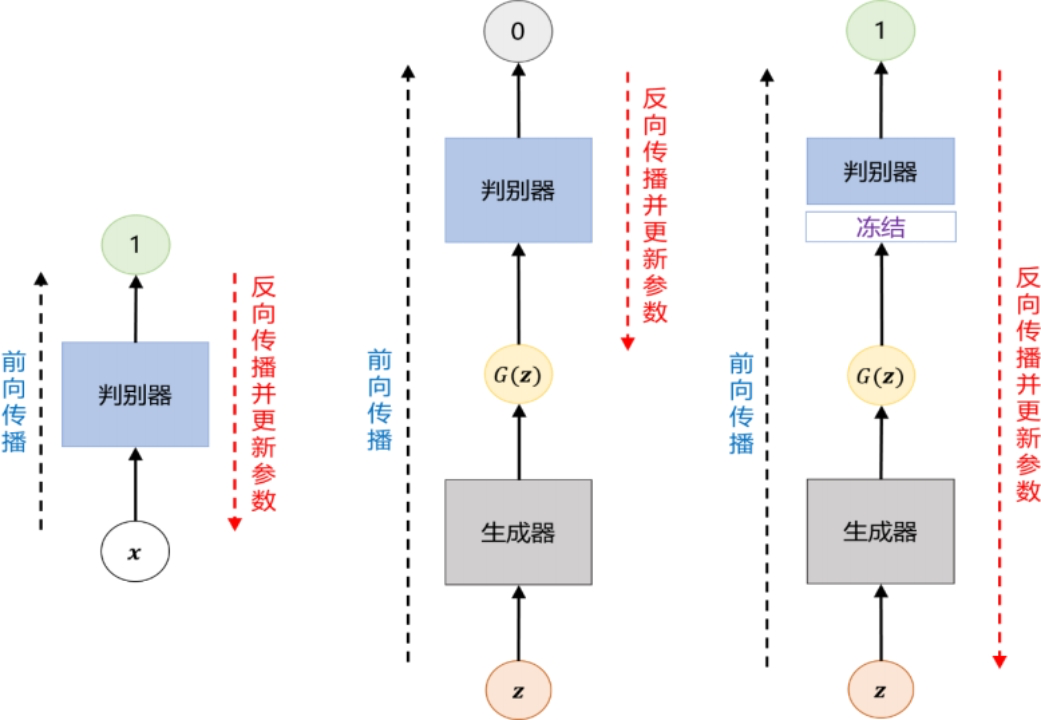
GAN的训练过程包含三个步骤：

1. 使用采样的真实数据𝒙训练判别器，即输入真实数据𝒙到判别器，前向传播，得到输出为1（表示判断结果为真），之后使用反向传播算法更新判别器的参数。
2. 使用生成器生成的数据𝐺(𝒛)训练判别器，即输入生成器生成的数据𝐺(𝒛)到判别器，前向传播，得到输出为0（表示判断结果为假），之后使用反向传播算法再次更新判别器的参数。
3. 最后，使用生成器生成的数据𝐺(𝒛)训练生成器，即输入生成器生成的数据𝐺(𝒛)到判别器，采用上一步训练好的判别器的参数（冻结判别器的参数）前向传播，得到输出为1（表示判断结果为真），之后使用反向传播算法更新生成器的参数，这一步的目的在于训练更好的生成器，以迷惑判别器，使之将生成器生成的数据判别为真。

在这个过程中，双方都极力优化自己的网络，从而形成竞争对抗，直到双方达到一个动态的平衡。此时，生成器生成的数据分布无限接近真实数据的分布，判别器判别不出输入的是真实数据还是生成的数据，输出概率都是百分之五十。

训练算法如下

GAN的优势和不足

优势

1. 任何一个可微分函数都可以参数化D和G（如深度神经网络）
2. 支持无监督方法实现数据生成，减少了数据标注工作
3. 生成模型G的参数更新不是来自于数据样本本身（不是对数据的似然性进行优化），而是来自于判别模型D的一个反传梯度。

不足

1. 无需预先建模，数据生成的自由度太大
2. 得到的是概率分布，但是没有表达式，可解释性差。
3. D与G训练无法同步，训练难度大，会产生梯度消失问题。