MATLAB非均匀网格梯度计算

在matlab中，gradient函数可以很方便的对均匀网格进行梯度计算，但是对于非均匀网格，但是gradient却无法求解非均匀网格的梯度，这一点我之前犯过错误。我之前以为在gradient函数中指定x，y等坐标，其求解的就是非均匀网格梯度了，然而并不是。

于是，今天下午开始写非均匀网格求梯度的函数。
首先，函数的要求为：
1、边界处采用二阶偏心差分
2、内部网格点采用二阶中心差分
3、计算三维矩阵的梯度

明确目标之后，我们首先进行理论推导：

理论推导

1、内部网格点

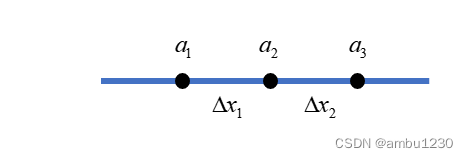
对a1和a3两点分别进行泰勒展开，公式如下：
$$\begin{gathered} a_3=a_2+{\dot{a}}_2\Delta x_2+\frac{1}{2}{\ddot{a}}_2\Delta x_2^2+O(\Delta x_2^3)\stackrel{◯}{1} \\ {a}_1=a_2-{\dot{a}}_2\Delta x_1+\frac{1}{2}{\ddot{a}}_2\Delta x_1^2+O(\Delta x_1^3)\stackrel{◯}{2} \end{gathered}$$

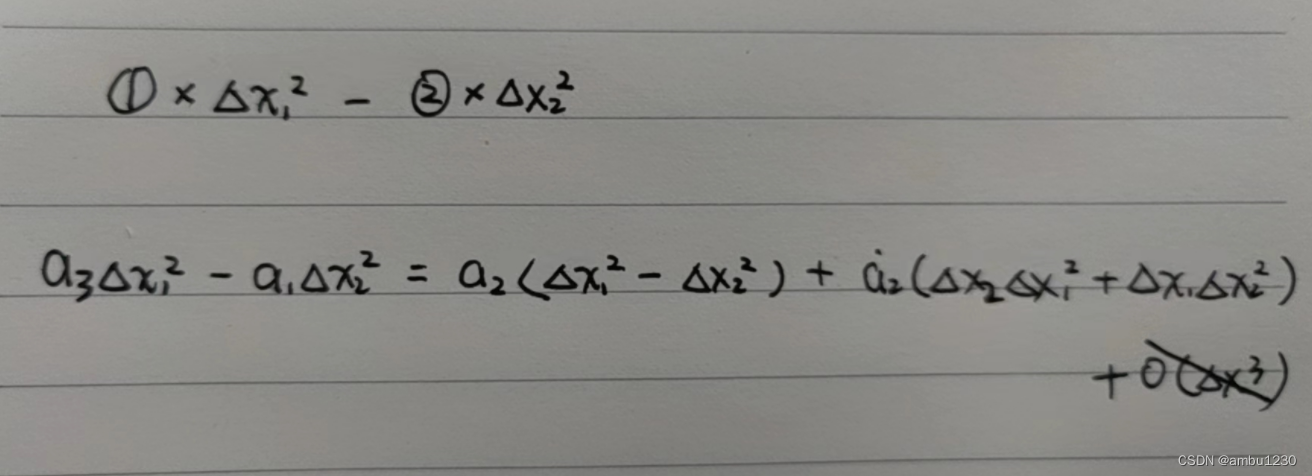
最终得到

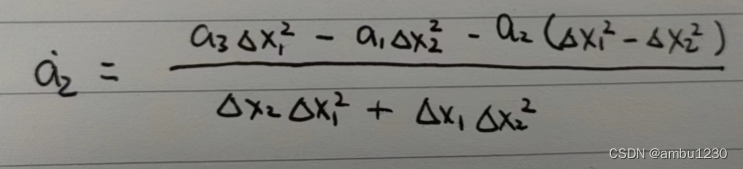
2、边界点

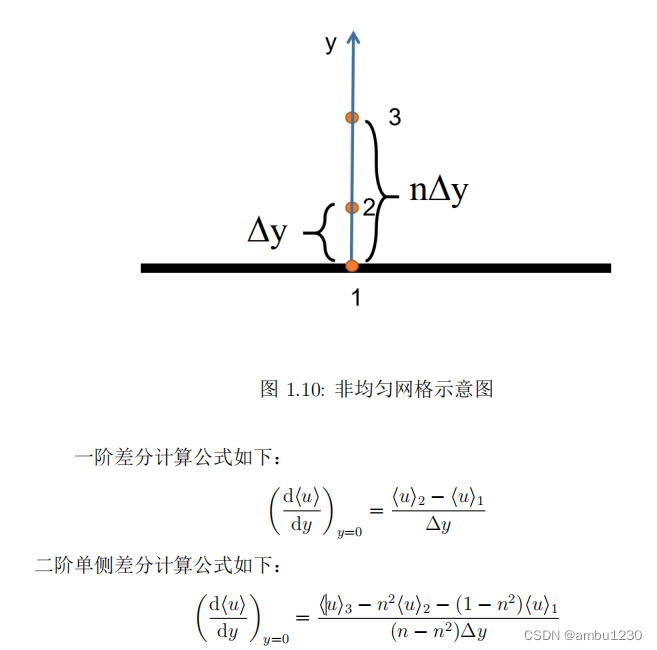
理论部分结束，下面进入代码部分

代码部分

首先，我写了一个1D的函数

function dydx = calc_grad_1D(x,y)
%% 求解一维数组的梯度
%% input1:一维函数坐标-->x
%% input2：一维函数值-->y
dydx = zeros(1,length(x));
for i = 1:length(x)
    if i>1 && i<length(x)
        deltax1 = x(i)-x(i-1);
        deltax2 = x(i+1)-x(i);
        son = (y(i+1)*deltax1^2-y(i-1)*deltax2^2-y(i)*(deltax1^2-deltax2^2));
        mom = (deltax2*deltax1^2+deltax1*deltax2^2);
        dydx(i) = son/mom;
    elseif i==1
        n = (x(3)-x(1))/(x(2)-x(1));
        son = y(i+2)-y(i+1)*n^2-(1-n^2)*y(i);
        mom = (n-n^2)*(x(i+1)-x(i));
        dydx(i)=son/mom;
    elseif i==length(x)
        n = (x(i)-x(i-2))/(x(i)-x(i-1));
        son = y(i-2)-y(i-1)*n^2-(1-n^2)*y(i);
        mom = (n-n^2)*(x(i)-x(i-1));
        dydx(i)=-son/mom;
    end
end
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

接下来验证该函数的准确性

x = [1 2 4 7 10];
y = x.^2;
%%
dydx = calc_grad_1D(x,y);
%%
dydx_ana = 2.*x;
plot(x,dydx_ana,'-*')
hold on
plot(x,dydx,'-o')
xlabel('x');ylabel('dydx')
legend('理论值','数值解')
1
2
3
4
5
6
7
8
9
10
11

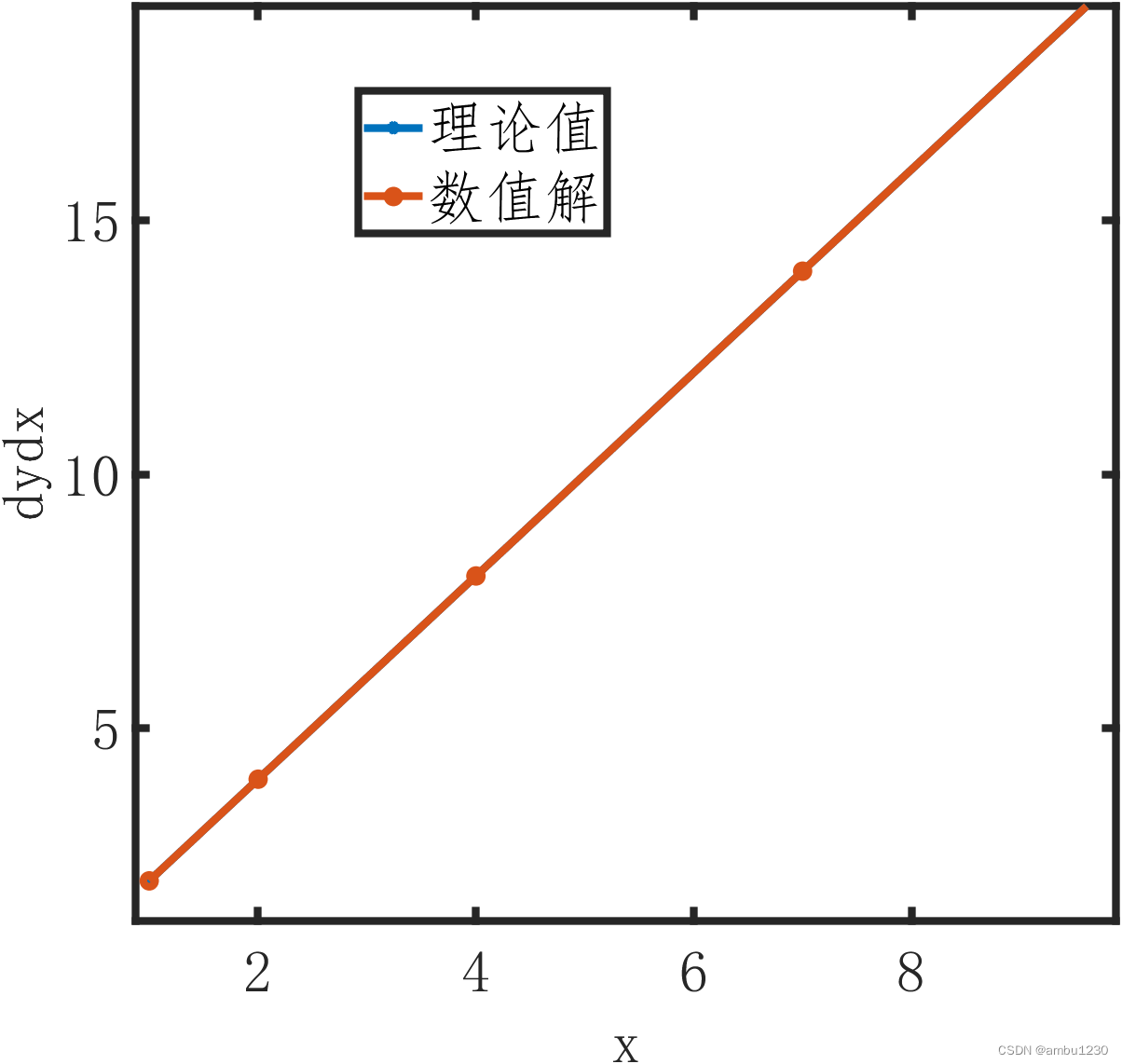
接下来我们进行3D矩阵的梯度求解，思想是调用上述的1D求解函数。
代码如下：

function [dfdx,dfdy,dfdz] = calc_grad_3D(F,X,Y,Z)
%UNTITLED26 此处提供此函数的摘要
%   此处提供详细说明
nx = size(X,1);ny = size(Y,2);nz = size(Z,3);
dfdx = zeros(nx,ny,nz);dfdy = zeros(nx,ny,nz);dfdz = zeros(nx,ny,nz);
for j = 1:ny
    for k = 1:nz
        dfdx(:,j,k) = calc_grad_1D(X(:,j,k),F(:,j,k));
    end
end
for i = 1:nx
    for k = 1:nz
        dfdy(i,:,k) = calc_grad_1D(Y(i,:,k),F(i,:,k));
    end
end
for i = 1:nx
    for j = 1:ny
        dfdz(i,j,:) = calc_grad_1D(Z(i,j,:),F(i,j,:));
    end
end
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

具体案例是求解函数$F=x^2+y^2+z^2$在三个方向的梯度

clc;clear
x = 1:10;y = x;z = x;
[X,Y,Z] = ndgrid(x,y,z);
F = X.^3+Y.^2+Z.^3;
%%
[dFdy,dFdx,dFdz] = gradient(F,Y(1,:,1),X(:,1,1),Z(1,1,:));
%%
[dfdx,dfdy,dfdz] = calc_grad_3D(F,X,Y,Z);
%% 理论解与数值解对比
dfdy_ana = 2.*(Y);
dfdy_ana = reshape(dfdy_ana,1000,1);
dfdy = reshape(dfdy,1000,1);
dFdy = reshape(dFdy,1000,1);
c = abs(dfdy-dfdy_ana);
d = abs(dFdy-dfdy_ana);
plot(c,'-o')
hold on
plot(d,'-o')
%% 绘图设置
axis([0 1000 0 2])
legend('My code','MATLAB gradient')
ylabel('误差')


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

结果如下：
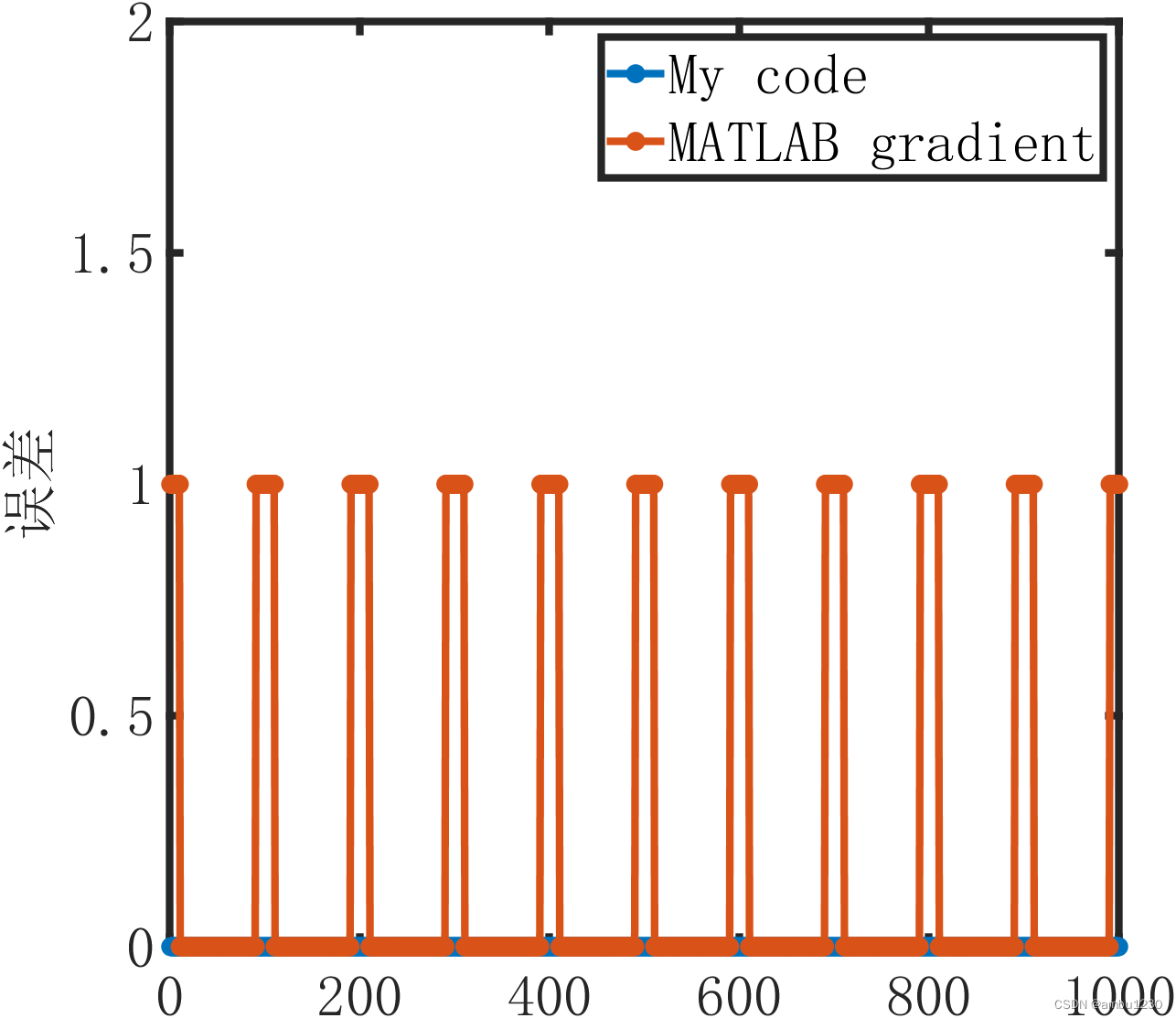可以看出，matlab里的gradient函数由于在边界上采用一阶差分，因此存在误差，而我们的函数内部点和边界点都采用二阶精度，因此误差为0。