数据结构 第六章 树与二叉树（一）

🚀 【考纲要求】树的基本概念

一、树的基本概念

1.1树的定义

如下所示就是一个树，需要知道树是递归的数据结构，同时树仍然是一个逻辑结构。（对于树是递归定义的数据结构，在后面我们会有更深刻的体会）

树的特点：

• 最上面的R称为树的根节点，树的根节点没有前驱，除去树的根节点以外的所有节点都有唯一的前驱节点。
• 树中的节点都有零个或者多个后继节点，对于树的最下面一排的节点，他们的后继节点都为零，即称之为树的叶子节点，其余的又有前驱节点又有后继节点的称为分支节点。

树这种逻辑结构适用于表示具有层次结构的数据，如我们电脑中的文件系统，采用的就是层次结构。

1.2 树中的基本术语

①祖先、子孙、双亲、孩子、兄弟、和堂兄弟。

• 祖先：以G节点为例，其祖先位D、A。

• 子孙：以A节点为例，其子孙是B、C、D、E、F、G。

• 双亲：以E节点为例，其双亲是B，B也叫做E的父节点。

• 孩子：以B节点为例，E、F就为其孩子节点。

• 兄弟：以B为例，其兄弟节点是B、C、D。

• 堂兄弟：以G为例，其唐兄弟节点是B、D。
  
  ②节点的度和树的度

• 📕 节点的度是其的孩子节点的个数；

• 📕 而树的度是一个树中节点度最大的度称为树的度。

下图中，其B节点的度为2，该树的度也是2，因为该树中节点的度最大为2。

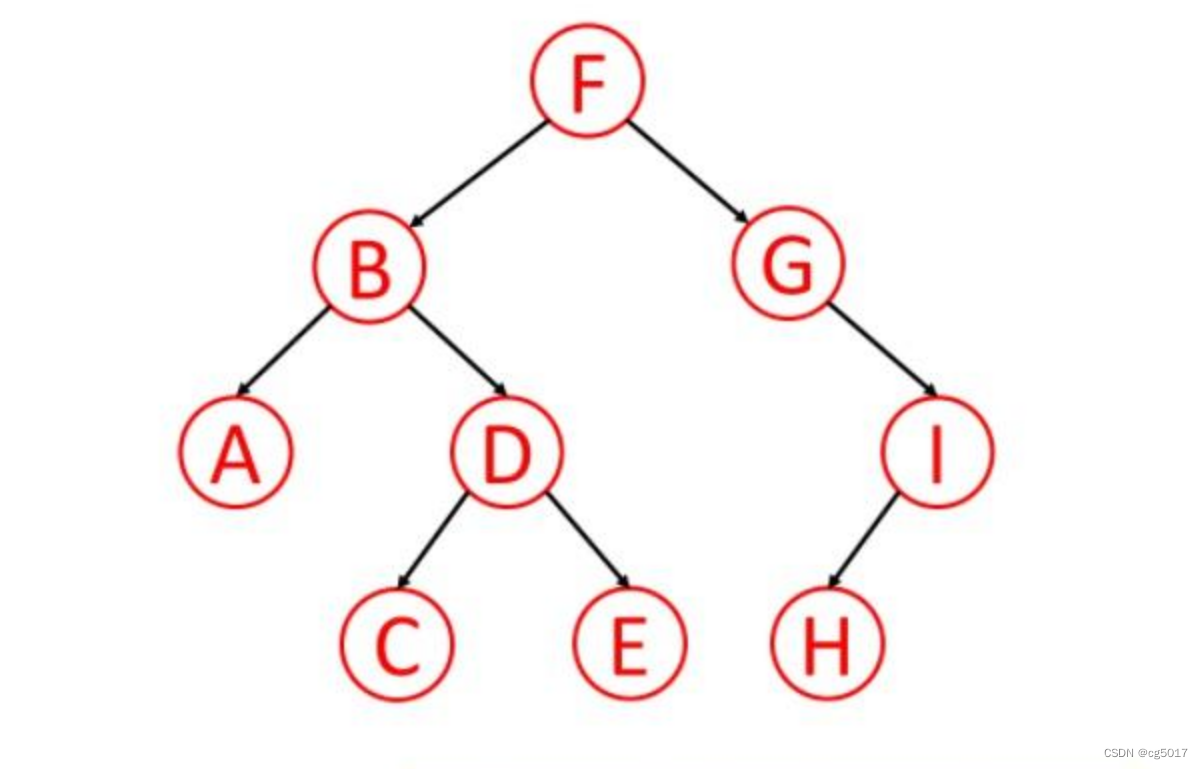
③分支节点、叶子节点、根节点

• ❀ 分支节点：他有前驱和后继节点。
• ❀ 叶子节点：只有前驱节点，无后继节点。
• ❀ 根节点：只有后继节点，无前驱节点。

仍然以上图为例，其中A、C、E、H为叶子节点，他们只有前驱节点；其中B、D、G、I是分支节点，他们既有前驱节点，也有后继节点；其中F为根节点，它没有前驱节点。

④节点的深度、节点的层次、树的高度、节点的高度

• ❀ 节点的层次：从上往下数，第一层、第二层、、、
• ❀ 节点的深度：就从上往下数，深度就是节点所在的层次。
• ❀ 树的高度：树总共有多少层。
• ❀ 节点的高度：是以该节点为根节点的子树的高度。

仍然以上图为例，其D节点的层次为第3层，该节点的深度为3。该树的高度为4；D的节点的高度为2。

⑤有序树和无序树

有序树就如下图所示，父亲、二叔、三叔的位置不能换、从左到右有顺序就为有序树。而无序树就是从左到右没有顺序，可以随意互换。

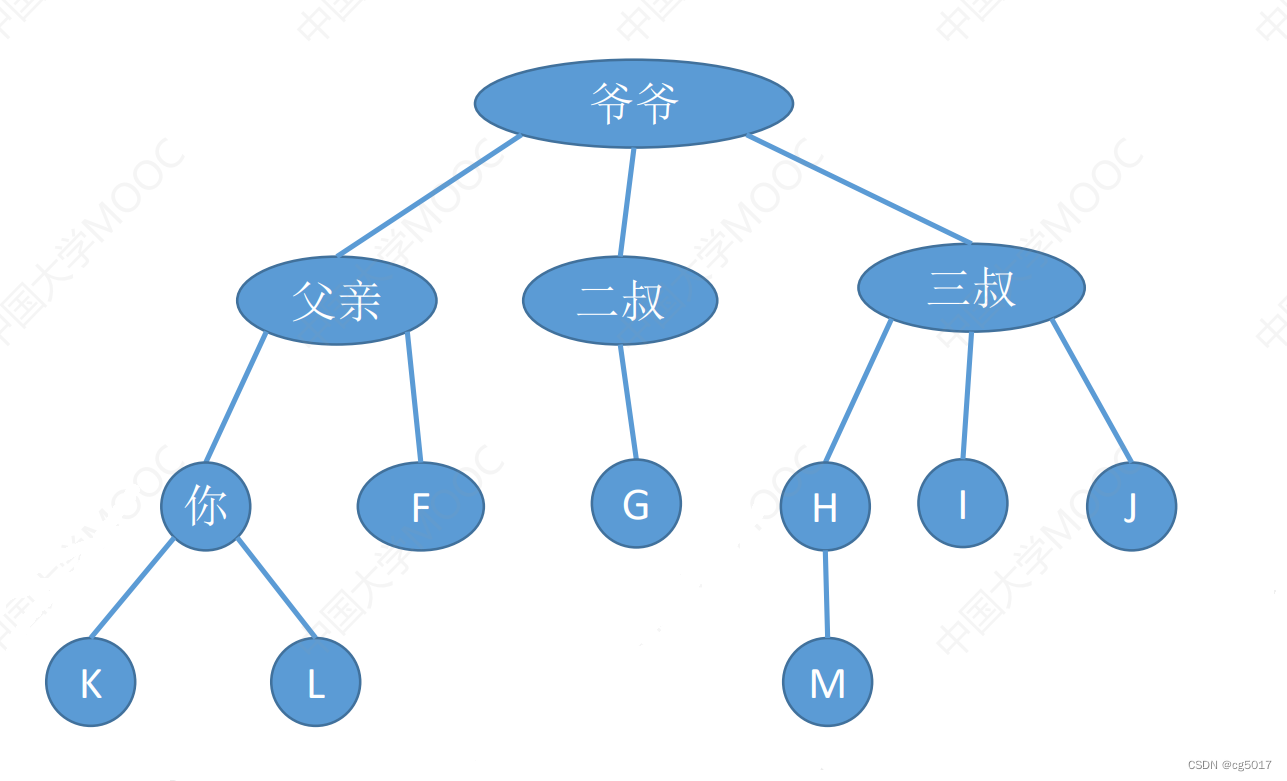
⑥路径和路径长度

• ❀ 路径是两个节点之间的节点，例如上图爷爷节点和你节点直接的路径为{父亲}。
• ❀而路径长度描述的从爷爷节点到你节点所要经过的边的个数，此时该路径长度就为2。

1.3树的性质

• ①树的节点数$n$等于所有节点度数之和加1。
• ②度为$m$的树中第$i$层上至多有$m^{i-1}$个节点
• ③高度为$h$的$m$叉树至多有$(m^h-1)/(m-1)$个节点。这个其实就是$m^0+m^1+m^2+...+m^{n-1}$，将每一个最多的给加起来。
• ④高度为$h$的$m$叉树至少有$h+m-1$个节点。
• ⑤度为$m$、具有$n$个节点的树的最小高度h如下计算公式。$$h=\lceil lo{g}_m(n(m-1)+1)\rceil$$
• ⑥度为$m$、具有$n$个节点的树的最大高度为$n-m+1$

Gamma公式展示 $\Gamma (n)=(n-1)!\forall n\in \mathbb{N}$ 是通过 Euler integral