C. Left and Right Houses

本题链接：Problem - C - Codeforces

题目：

样例：

7
3
101
6
010111
6
011001
3
000
3
110
3
001
4
1100

思路：

        根据题目意思。

        寻找一条道路进行分割该字符串，设该道路分割位置为 i  ，使得满足以下条件：

        1、左侧有 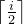   个  0，右侧有  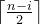个 1

        2、如果有多个位置满足 条件一，我们就要选择最小的位置 .

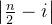        读懂意思后，暴力枚举一遍即可。通过前缀和记录每个位置 1 的数量，遍历判断以下即可。

代码详解如下：

#include 
#include 
#include 
#include 
#include 
#include 
#define endl '\n'
#define int long long
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;
inline void solve();
 
signed main()
{
//	freopen("a.txt", "r", stdin);
	IOS;
	int _t = 1;
	cin >> _t;
	while (_t--)
	{
		solve();
	}
	return 0;
}
 
inline void solve()
{
	string s;
	int n,ans = -1;
	cin >> n >> s;
	vector<int>sum(n + 10,0);
	
	// 这里是根据前缀和记录相应位置 1 的数量
	// 这里从下标 1 开始记录的前缀和数量，是由于 道路有可能会在最左侧。
	for(int i = 1;i <= n;++i)
	{
		sum[i] = sum[i - 1] + bool(s[i - 1] == '1');
	}
	
	// 开始遍历判断 这里 i <= n 是有可能道路也会在最右侧
	for(int i = 0;i <= n;++i)
	{
		// 如果 道路是 i 的时候，左侧 1 的数量没有超过 i / 2  说明 左侧至少有 i / 2 个 0
		// 并且  右侧 1 的个数  >= (n - i) / 2 那么满足了 条件一
		if((sum[i] << 1) <= i and ((sum[n] - sum[i]) << 1) >= n - i)
		{
			// 这里是判断寻找最小化位置 |n / 2 - i|
			if(abs(n - (i << 1)) < abs(n - (ans << 1))) ans = i;
		}
	}
	cout << ans << endl;
}

最后提交：