3、你真的把MPC搞懂了吗

        MPC是模型预测控制（Model Predictive Control）的缩写，也叫做滚动时域控制（receding horizon control）。在机器人领域，MPC主要应用于运动控制和路径规划、轨迹跟踪。

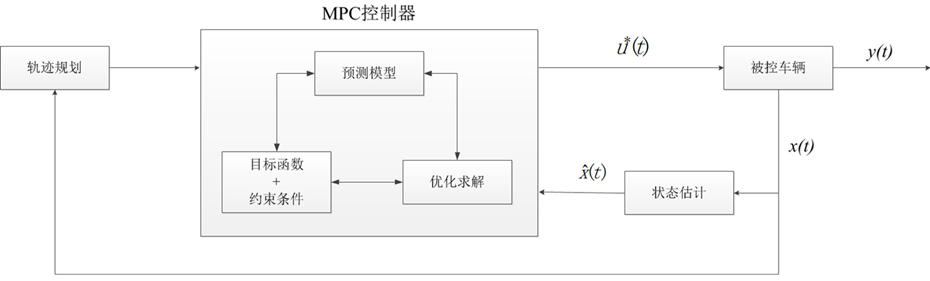
一、组成部分：
        1、模型：要解决问题的对象所在领域的模型，数学上表现为问题对象的状态和输入控制量。以小车轨迹跟踪为例，包括小车的位置、方向，控制小车需要的转向和速度，以及与运动相关的公式，如路程、速度、时间、加速度相关的公式。
        2、预测：根据已有的模型、系统当前的状态、期望的状态和未来的控制量，来预测系统未来的输出。接上例，由小车当前的位置和方向，需要到达的目标位置，未来施加的速度和转向角，来预测小车下一时刻的位置、方向和速度、转向角。一般会输出未来一个时间段上的多个值，这个未来时间段就叫预测区间（Predictive Horizon）。
        3、控制：将预测的输出与期望的输出做比较，要使得这个差别最小化，这就是代价函数。施加一些约束条件，通过优化的方法，优化出未来控制量，使得代价函数最小。最后只取多个输出值中的第一个值。接上例，执行小车代价函数后，得到多个时刻的位置、方向和速度、转向角，只取第一个时刻的值来控制小车，保证汽车始终保持在道路中央。

二、案例说明 

1、以无人车轨迹跟踪为例，建立模型；

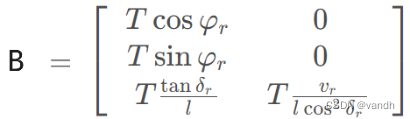C, Q, Qf, R矩阵等；

X上面1点是路程一次求导为速度，2点是加速度；

三、一言不合（说不清楚）上代码

将江湖流传的代码进行了面向对象的封装，并删繁就简，去掉了许多不便理解的无用的边角料算法与变量，修复了一些bug，加上了详细得令人发指的注解，希望能一码绝后尘，

• Q，Qf：状态偏差代价矩阵（最终），不同的运动模型值不一样；
•         R：输入偏差代价矩阵，不同的运动模型值不一样；

  • 2、求状态偏差Ẋ和控制量偏差u。

    x,y,fai=平面坐标，偏航角；v，delta=速度，前轮转角；

    其中ẋ是当前状态的平面x坐标, xr是期望状态的平面x坐标，其它类推；

  • 

  • 3、计算代价函数与约束

  • 

• N：时间范围(Time Horizon)，即预测的区间，包含N个时间段；
• Ẋ(k)TQẊ(k)：衡量状态偏差
• u(k)TRu(k)：衡量输入大小
• Ẋ(N)TQfẊ(k)：衡量最终状态偏差
• X(k+1)是在k+1时刻的系统状态，uk是k时刻的控制量。

三、一言不合（说不清楚）上代码

        把江湖上流传最广的MPC代码进行了面向对象的封装，修正了一些小bug，去掉了一些令人难以理解的边角料变量和小算法，完美贴合了第二部分的理论，特别是加入了令人详细得发指的注解，希望能一码绝后码，成为全网最易理解的源码实现，拿走不谢，不解可询。

from celluloid import Camera
import numpy as np
import matplotlib
matplotlib.use('TkAgg') # matplotlib切换图形界面显示终端TkAgg
import matplotlib.pyplot as plt
import cvxpy
import math
import sys
 
#一、无人车轨迹跟踪运动学模型
class Vehicle:
    def __init__(self):  # 车辆
        self.x = 0  # 初始x
        self.y = -4  # 初始y
        self.psi = 0  # 初始航向角
        self.v = 2  # 初始速度
        self.av = 1 # 加速度，为0就是恒速；
        self.L = 2 # 车辆轴距，单位：m
        self.dt = 0.1  # 时间间隔，单位：s
        self.R = np.diag([0.1, 0.1])  # [[0.1,0],[0,0.1]]  input cost matrix, 控制区间的输入权重，输入代价矩阵，Ru(k)
        self.Q = np.diag([1, 1, 1])  # state cost matrix 预测区间的状态偏差，给定状态代价矩阵， Qx(k)
        self.Qf = np.diag([1, 1, 1])  # state final matrix = 最终状态代价矩阵
        self.MAX_STEER = np.deg2rad(45.0)  # maximum steering angle [rad] 最大转向角
        self.MAX_VEL = 100.0  # maximum accel [m/s]  最大速度
 
    def update_state(self, delta_f):
        self.x = self.x+self.v*math.cos(self.psi)*self.dt
        self.y = self.y+self.v*math.sin(self.psi)*self.dt
        self.psi = self.psi+self.v/self.L*math.tan(delta_f)*self.dt
        self.v = self.v + self.av * self.dt
 
    def get_state(self):
        return self.x, self.y, self.psi, self.v
 
    def state_space(self, ref_delta, ref_yaw):
        """Args: ref_delta (_type_): 参考的转角控制量;  ref_yaw (_type_): 参考的偏航角 """
        A = np.matrix([
            [1.0, 0.0, -self.v * self.dt*math.sin(ref_yaw)],
            [0.0, 1.0, self.v * self.dt*math.cos(ref_yaw)],
            [0.0, 0.0, 1.0]])
        B = np.matrix([
            [self.dt*math.cos(ref_yaw), 0],
            [self.dt*math.sin(ref_yaw), 0],
            [self.dt*math.tan(ref_delta)/self.L, self.v*self.dt /(self.L*math.cos(ref_delta)*math.cos(ref_delta))]
        ])
        C = np.eye(3)  # 3x3的单位矩阵
        return A, B, C
 
# 二、道路模型，虚拟道路上1000个点，给出每个点的位置（x坐标, y坐标，轨迹点的切线方向, 曲率k）
class VPath:
    def __init__(self, util):
        self.refer_path = np.zeros((1000, 4))
        self.refer_path[:, 0] = np.linspace(0, util.x_xis, 1000)  # x 间隔起始点、终止端，以及指定分隔值总数，x的间距为0.1
        self.refer_path[:, 1] = 2*np.sin(self.refer_path[:, 0]/3.0) + 2.5*np.cos(self.refer_path[:, 0]/2.0)  # y
        # 使用差分的方式计算路径点的一阶导和二阶导，从而得到切线方向和曲率
        for i in range(len(self.refer_path)):
            if i == 0:
                dx = self.refer_path[i+1, 0] - self.refer_path[i, 0]
                dy = self.refer_path[i+1, 1] - self.refer_path[i, 1]
                ddx = self.refer_path[2, 0] + self.refer_path[0, 0] - 2*self.refer_path[1, 0]
                ddy = self.refer_path[2, 1] + self.refer_path[0, 1] - 2*self.refer_path[1, 1]
            elif i == (len(self.refer_path)-1):
                dx = self.refer_path[i, 0] - self.refer_path[i-1, 0]
                dy = self.refer_path[i, 1] - self.refer_path[i-1, 1]
                ddx = self.refer_path[i, 0] + self.refer_path[i-2, 0] - 2*self.refer_path[i-1, 0]
                ddy = self.refer_path[i, 1] + self.refer_path[i-2, 1] - 2*self.refer_path[i-1, 1]
            else:
                dx = self.refer_path[i+1, 0] - self.refer_path[i, 0]
                dy = self.refer_path[i+1, 1] - self.refer_path[i, 1]
                ddx = self.refer_path[i+1, 0] + self.refer_path[i-1, 0] - 2*self.refer_path[i, 0]
                ddy = self.refer_path[i+1, 1] + self.refer_path[i-1, 1] - 2*self.refer_path[i, 1]
            self.refer_path[i, 2] = math.atan2(dy, dx)  # yaw
            self.refer_path[i, 3] = (ddy * dx - ddx * dy) / ((dx ** 2 + dy ** 2)**(3 / 2))  # 曲率k计算
 
# 三、MPC
class MPC:
    def __init__(self):
        self.NX = 3  # 状态x = x, y, yaw = x，y坐标，偏航角
        self.NU = 2  # 输入变量u = [v, delta] = [速度，前轮转角]
        self.T = 8  # horizon length  预测区间=时间范围=8个dt
 
    """找出车辆当前实际位置(x,y)与距离道路最近的点
    返回结果：将计算出的横向误差 e、曲率 k、最近目标位置所在路径段处的航向角yaw 和最近目标位置所在路径段的下标 s
    """
    def calc_track_error(self, util, path, x, y):
        # 计算小车当前位置与参考路径上每个点之间的距离，找到距离小车最近的参考路径点，将该点的下标保存为 s
        d_x = [path.refer_path[i, 0]-x for i in range(len(path.refer_path))]
        d_y = [path.refer_path[i, 1]-y for i in range(len(path.refer_path))]
        d = [np.sqrt(d_x[i]**2+d_y[i]**2) for i in range(len(d_x))]
        s = np.argmin(d)  # 求最小值对应的索引
        yaw = path.refer_path[s, 2]
        k = path.refer_path[s, 3]  # 将参考路径上距离小车最近的点的曲率 k 作为小车所在路径段的曲率
        # 将小车当前位置与距离最近的参考路径点之间的连线,与参考路径在该点处的方向角之差,作为小车当前位置与参考路径之间的方向角误差 angle。
        angle = util.normalize_angle(yaw - math.atan2(d_y[s], d_x[s]))
        e = d[s]  # 将小车当前位置与参考路径上距离最近的点之间的距离作为小车的横向误差 e
        if angle < 0:  # 根据 angle 的符号将横向误差 e 取正或取负：如果 angle 小于 0，则将横向误差 e 取负
            e *= -1
        return k, s
 
    """由当前小车的位置实际值(x,y)，取离道路最近的几个目标值
        参数：robot_state是车辆的当前状态(x,y,yaw,v); 
        返回值：xref=3行9列共九段预测区间的(x,y,yaw), ind=当前路径段的下标, dref=二行八列(v, 前轮转角)
    """
    def calc_ref_trajectory(self, util, vehicle, path, robot_state):
        # 曲率 k、小车所在路径段的下标 s
        k, ind = self.calc_track_error(util, path, robot_state[0], robot_state[1])
        # 初始化参考轨迹：定义一个 3 行 T+1=9 列的数组 xref，用于存储参考轨迹。将第一列的值设为当前小车位置所在路径段的值(x,y,yaw)
        xref = np.zeros((self.NX, self.T + 1))
        ncourse = len(path.refer_path)  # 1000
        # 参考控制量，由车辆轴距和曲率，计算前轮转角
        ref_delta = math.atan2(vehicle.L*k, 1)
        # 二行八列 的第 0 行所有列车速，第 1 行所有列是转角
        dref = np.zeros((self.NU, self.T))
        dref[0, :] = robot_state[3]
        dref[1, :] = ref_delta
        travel = 0.0
        for i in range(self.T + 1):
            if (ind + i) < ncourse:
                xref[0, i] = path.refer_path[ind + i, 0]  # x坐标
                xref[1, i] = path.refer_path[ind + i, 1]  # y坐标
                xref[2, i] = path.refer_path[ind + i, 2]  # v速度
        return xref, ind, dref
 
    """
    通过二次线性规划算法，由几个目标点的状态和控制量，计算未来最优的几个点的状态和控制量
    xref: reference point=shape(3,9)=(x,y,yaw; 0~8)
    x0: initial state，(x,y,yaw), 
    delta_ref: reference steer angle 参考转向角 =(2,8)=(v,转角；0~7 )
    ugv:车辆对象
    mpc控制的代价函数 
        minJ(U)=sum(u^T R u + x^T Q x + x^T Qf x)
    约束条件 
        x(k+1) = Ax(k) + Bu(k) + C
        x(k)=[x-xr, y-yr, yaw-yawr]
        u(k)=[v-vr, delta-deltar]
        x(0)=x0
        u(k)<=umax
    """
    def linear_mpc_control(self, util, vehicle, xref, x0, delta_ref):
        x = cvxpy.Variable((self.NX, self.T + 1))  # 定义状态变量9维向量x，具体数值不确定
        u = cvxpy.Variable((self.NU, self.T))      # 定义控制变量 u=[速度，前轮转角]
        cost = 0.0  # 代价函数
        constraints = []  # 约束条件
        for t in range(self.T):
            cost += cvxpy.quad_form(u[:, t] - delta_ref[:, t], vehicle.R)  # 衡量输入大小=u^T R u
            if t != 0:
                cost += cvxpy.quad_form(x[:, t] - xref[:, t], vehicle.Q)  # 衡量状态偏差=x^T Q x
            A, B, C = vehicle.state_space(delta_ref[1, t], xref[2, t]) # (转角，偏航角)
            constraints += [x[:, t + 1]-xref[:, t+1] == A @ (x[:, t]-xref[:, t]) + B @ (u[:, t]-delta_ref[:, t])]
        cost += cvxpy.quad_form(x[:, self.T] - xref[:, self.T], vehicle.Qf)  # 衡量最终状态偏差=x^T Qf x
 
        constraints += [(x[:, 0]) == x0]
        constraints += [cvxpy.abs(u[0, :]) <= vehicle.MAX_VEL]
        constraints += [cvxpy.abs(u[1, :]) <= vehicle.MAX_STEER]
        # 定义了一个“问题”，“问题”函数里填写凸优化的目标，目前的目标就是cost最小
        prob = cvxpy.Problem(cvxpy.Minimize(cost), constraints)
        # 求解，运行完这一步才能确定x的具体数值
        prob.solve(solver=cvxpy.ECOS, verbose=False)
        # # prob.value储存的是minimize(cost)的值，就是优化后目标的值; 查看变量x使用x.value
        if prob.status == cvxpy.OPTIMAL or prob.status == cvxpy.OPTIMAL_INACCURATE:
            opt_x = util.get_nparray_from_matrix(x.value[0, :])
            opt_y = util.get_nparray_from_matrix(x.value[1, :])
            opt_yaw = util.get_nparray_from_matrix(x.value[2, :])
            opt_v = util.get_nparray_from_matrix(u.value[0, :])
            opt_delta = util.get_nparray_from_matrix(u.value[1, :])
        else:
            opt_v, opt_delta, opt_x, opt_y, opt_yaw = None, None, None, None, None,
        return opt_v, opt_delta, opt_x, opt_y, opt_yaw
 
# 工具类
class Util:
    def __init__(self):
        self.x_xis = 100  # x轴的长度100,共1000个点
    # 展示动图
    def draw(self, ugv, path, mpc):
        x_ = []
        y_ = []
        fig = plt.figure(1)  # 图像编号1
        for i in range(sys.maxsize):
            robot_state = np.zeros(4)  # [0, 0, 0, 0]
            robot_state[0] = ugv.x
            robot_state[1] = ugv.y
            robot_state[2] = ugv.psi
            robot_state[3] = ugv.v
            x0 = robot_state[0:3]
            xref, target_ind, dref = mpc.calc_ref_trajectory(self, ugv, path, robot_state)
            opt_v, opt_delta, opt_x, opt_y, opt_yaw = mpc.linear_mpc_control(self, ugv, xref, x0, dref)
            # 速度v与x,y坐标不需要传递，只能按车辆指定的速度来计算
            ugv.update_state(opt_delta[0])
            x_.append(ugv.x)
            y_.append(ugv.y)
 
            plt.cla()  # cla清理当前的axes，以下分别绘制蓝色-.线，红色-线，绿色o点
            plt.plot(path.refer_path[:, 0], path.refer_path[:, 1], "-.b",  linewidth=1.0, label="course")
            plt.plot(x_, y_, "-g", label="trajectory")
            plt.plot(x_, y_, ".r", label="target")
            plt.grid(True)  # 显示网格线 1=True=默认显示；0=False=不显示
            plt.pause(0.001) # 图形会间隔0.001秒后重新绘制
            if ugv.x > self.x_xis:  # 判断是否到达最后一个点
                break
 
    # Normalize an angle to [-pi, pi]
    def normalize_angle(self, angle):
        while angle > np.pi:
            angle -= 2.0 * np.pi
        while angle < -np.pi:
            angle += 2.0 * np.pi
        return angle
 
    def get_nparray_from_matrix(self, x):
        return np.array(x).flatten()
 
if __name__=='__main__':
    util = Util()
    ugv = Vehicle()
    path = VPath(util)
    mpc = MPC()
    util.draw(ugv, path, mpc)