时间复杂度和空间复杂度

引言：本篇博客介绍了时间复杂度和空间复杂度的基本概念，并且附带有各种例题加深理解，有问题欢迎私信或者评论区讨论，如果有帮助，希望大家点赞👍评论和收藏。

        更多有关C语言的知识详解可前往个人主页：计信猫

一，时间复杂度

1，时间复杂度的定义

        时间复杂度：算法的时间复杂度是一个函数，它表示着某算法中的基本操作执行的次数。

        我们来看一个例题：请问该函数中++count执行了多少次？

// 请计算一下Func1中++count语句总共执行了多少次？
void Func1(int N)
{
	int count = 0;
	for (int i = 0; i < N; ++i)
	{
		for (int j = 0; j < N; ++j)
		{
			++count;
		}
	}
 
	for (int k = 0; k < 2 * N; ++k)
	{
		++count;
	}
	int M = 10;
	while (M--)
	{
		++count;
	}
	printf("%d\n", count);
}

        从该函数中，我们不难看出，++count的执行次数与形参N有关，因此不难写出++count的执行次数F（N）与形参N的关系了。

        但是在我们实际进行时间复杂度的计算时，我们并不需要十分精确的N值来进行计算，我们只需要使用大O的渐进表示法对时间复杂度进行表示就可以了。

2，大O的渐进表示法

        大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。推到大O的方法遵循着三条法则：

法则1：用常数1取代运行时间中的所有加法常数。

例：请计算下列函数中++count的执行次数

// 请计算一下Func2中++count语句总共执行了多少次？
void Func2(int N)
{
	int count = 0;
	int M = 10;
	while (M--)
	{
		++count;
	}
	printf("%d\n", count);
}

        在该函数中我们不难看出，++count的执行次数为10次，所以该函数的F（N）=10为常数，那么该函数的大O的渐进表示法为O（1）。

 法则2：在修改后的运行次数函数中，只保留最高阶项。

         在程序的运行之中，如果我们的N值比较小的时候，其实不同的代码的运行速度都不会有太大的差异，那么就无法比较不同代码算法的时间效率。所以我们一般都会将N视为无穷大，而当N无穷大时，我们就只需要保留F（N）函数中的最高阶项，其他的项相较于最高阶项来说影响较小，故可以忽略省去。

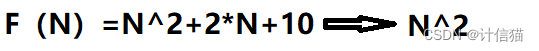
        如图该函数的最高阶项为N^2,故我们只保留最高阶项，那么时间复杂度则为O（N^2）。

法则3：如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

例：请计算下列函数中++count的执行次数

// 请计算一下Func3中++count语句总共执行了多少次？
void Func3(int N)
{
	int count = 0;
	for (int k = 0; k < 2 * N; ++k)
	{
		++count;
	}
}

         显而易见，该函数的F（N）=2*N，而当我们进行大O阶的推导时，N为无穷大，那么此时系数2的影响非常的小，那么我们可以直接忽略，故该函数的时间复杂度为O（N）。

3，时间复杂度为最坏情况

算法的时间复杂度存在最好、平均和最坏情况：
• 最坏情况：任意输入规模的最大运行次数(上界)
• 平均情况：任意输入规模的期望运行次数
• 最好情况：任意输入规模的最小运行次数(下界) 

 让我们先来一个简单的例子：计算strchr的时间复杂度

// 计算strchr的时间复杂度？
const char * strchr ( const char * str, int character );
//即查找一个字符串中某个字符

        而在这个函数中，则存在着上文所提到的三种情况：

• 最坏情况：字符串中最后一个才为该字符或者根本不存在该字符
• 平均情况：在字符串的中间个数找到该字符
• 最好情况：第一个就为所要寻找的字符

        在实际中一般情况关注的是算法的最坏运行情况，所以该函数搜索某字符的时间复杂度为O(N) 。

4，时间复杂度的计算例题

Ⅰ，冒泡排序的时间复杂度

冒泡排序的函数代码如下：

// 计算BubbleSort的时间复杂度
void BubbleSort(int* a, int n)
{
	assert(a);
	for (size_t end = n; end > 0; --end)
	{
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

        那我们可以知道，冒泡排序的最好和最坏情况如下：

        所以我们以最坏的情况进行讨论，F（N）则可以使用等差数列的公式进行计算，最后根据大O的推导法则可以得到冒泡排序的时间复杂度为O（N^2）。

 Ⅱ，二分查找的时间复杂度

二分查找的代码如下：

// 计算BinarySearch的时间复杂度
int BinarySearch(int* a, int n, int x)
{
	assert(a);
	int begin = 0;
	int end = n - 1;
	// [begin, end]：begin和end是左闭右闭区间，因此有=号 
    while (begin <= end)
	{
		int mid = begin + ((end - begin) >> 1);
		if (a[mid] < x)
			begin = mid + 1;
		else if (a[mid] > x)
			end = mid - 1;
		else
			return mid;
	}
	return -1;
}

        所以我们依然可以列出二分查找的最好与最坏情况：

        所以最坏的情况可以表示为：

•N/2/2/2……/2=1 

        那么假如查找了x次，就除以了x个2，则二分查找的时间复杂度为O（logN）。(ps：logN在算法分析中底数为2) 

二，空间复杂度

1，空间复杂度的定义

        空间复杂度：算法的空间复杂度也是一个函数，它表示的是为解决某个问题所需要的变量个数。   

        当然，空间复杂度也遵循前面所讲到的大O的渐进表示法。由于现在的科技发展，内存的缺少的问题逐渐得到解决，进而导致空间复杂度不为我们对某个算法的算法效率的主要考虑因素。对于某个算法的算法效率，我们还是以时间复杂度为主。

2，空间复杂度的计算例题

例题：冒泡排序的空间复杂度为多少？

// 计算BubbleSort的空间复杂度
void BubbleSort(int* a, int n)
{
	assert(a);
	for (size_t end = n; end > 0; --end)
	{
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

        显而易见，我们为了成功进行冒泡排序，我们创建了end，i，exchange三个变量，所以这个函数的空间复杂度为常熟，则为O（1）。