-
数据结构——二叉树
目录
前言
我们之前讲了二叉树的顺序存储的一种——堆,今天我们来了解二叉树的链式存储。了解二叉树的遍历,和二叉树的节点。通过递归分治的思想来实现二叉树的功能。
一、二叉树链式结构
为了先了解到二叉树的基本操作,我们先手动创造一个二叉树(与后面的二叉树的创建无关)。等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
二叉树的节点:
- typedef int BTDataType;
- typedef struct BTDataType {
- BTDataType val;
- struct BTDataType* left;//左子树
- struct BTDataType* right;//右子树
- }BTNode;
创建一个节点:
- // 创建节点
- BTNode* BuyNode(BTDataType x) {
- BTNode* n = (BTNode*)malloc(sizeof(BTNode));
- if (n == NULL)
- {
- perror("malloc fail");
- }
- n->val = x;
- n->right = n->left = NULL;
- return n;
- }
现在我们可以手动创建一个二叉树了
- //手动创建树
- BTNode* CreatBinaryTree()
- {
- BTNode* n1 = BuyNode(1);
- BTNode* n2 = BuyNode(2);
- BTNode* n3 = BuyNode(3);
- BTNode* n4 = BuyNode(4);
- BTNode* n5 = BuyNode(5);
- BTNode* n6 = BuyNode(6);
- n1->left = n2;
- n1->right = n4;
- n2->left = n3;
- n4->left = n5;
- n4->right = n6;
- return n1;
- }
再看二叉树基本操作前,再回顾下二叉树的概念,二叉树是:1. 空树2. 非空:根节点,根节点的左子树、根节点的右子树组成的。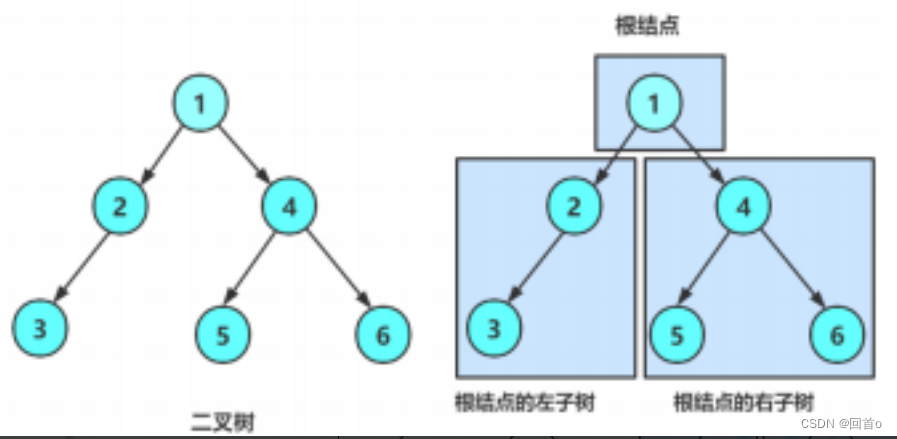
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
二、二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉 树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历 是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。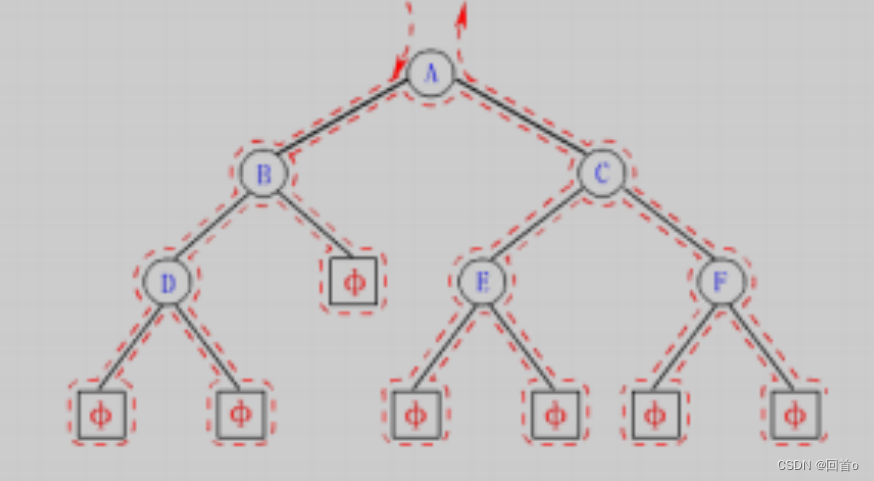 按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:1. 前序遍历 (Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。2. 中序遍历 (Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。3. 后序遍历 (Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:1. 前序遍历 (Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。2. 中序遍历 (Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。3. 后序遍历 (Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。- // 二叉树前序遍历
- void PreOrder(BTNode* root);
- // 二叉树中序遍历
- void InOrder(BTNode* root);
- // 二叉树后序遍历
- void PostOrder(BTNode* root);
2.1 前序遍历
- // 二叉树前序遍历
- void PreOrder(BTNode* root) {
- if (root == NULL)
- {
- printf("N ");
- return;
- }
- printf("%d ", root->val);
- PreOrder(root->left);
- PreOrder(root->right);
- }
前序遍历的遍历顺序为:根 左子树 右子树

2.2 中序遍历
- //二叉树中序遍历
- void InOrder(BTNode* root) {
- if (root == NULL)
- {
- printf("N ");
- return;
- }
- InOrder(root->left);
- printf("%d ", root->val);
- InOrder(root->right);
- }
中序遍历的遍历顺序为:左子树 根 右子树
2.3 后序遍历
- // 二叉树后序遍历
- void PostOrder(BTNode* root) {
- if (root == NULL)
- {
- printf("N ");
- return;
- }
- PostOrder(root->left);
- PostOrder(root->right);
- printf("%d ", root->val);
- }
后序遍历的遍历顺序为:左子树 右子树 根
三种遍历的运行结果为(其中N代表节点为空):

2.4 层序遍历
除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在 层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
与上面三种通过递归来遍历二叉树的不同,层序遍历使用的循环来遍历二叉树。
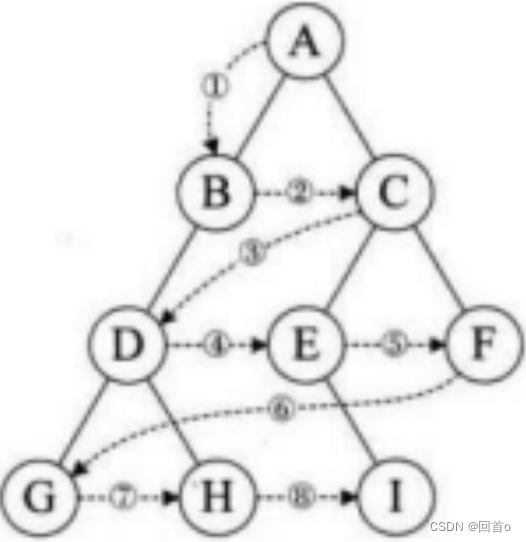
为了实现二叉树的层序遍历,我们通过之前学到的队列先进先出的特性来实现。
- //层序遍历
- void BinaryTreeLevelOrder(BTNode* root) {
- Queue pq;//创建队列
- QueueInit(&pq);
- if (root != NULL)
- QueuePush(&pq, root);
- while (!QueueEmpty(&pq))
- {
- BTNode* foront = QueueFront(&pq);//保存根节点
- QueuePop(&pq);
- if (foront != NULL)
- {
- printf("%d ", foront->val);//根节点出队列它的左右子树入队列
- QueuePush(&pq, foront->left);
- QueuePush(&pq, foront->right);
- }
- else
- {
- printf("N ");
- }
- }
- QueueDestroy(&pq);
- }
运行结果:

三、二叉树的节点
了解到二叉树的遍历后,我们来求二叉树节点个数以及高度等,实现这些我们需要理解递归分治。
找到递归子问题和返回条件(最小子问题)
以下图为例:

3.1 二叉树节点个数
- // 二叉树节点个数
- int BinaryTreeSize(BTNode* root) {
- return root==NULL?0:BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
- }
递归子问题:找根的左右子树的节点数
返回条件:当节点为空时

3.2 二叉树的深度
- int BinaryTreedepth(BTNode* root)
- {
- if (root == NULL)
- return 0;
- int leftdepth = BinaryTreedepth(root->left);
- int rightdepth = BinaryTreedepth(root->right);
- return leftdepth > rightdepth ? leftdepth + 1 : rightdepth + 1;
- }
递归子问题:找左右子树的深度最大的
返回条件:当节点为空时
注意:返回时本节点深度也要算,即返回深度要加1。

3.3 二叉树叶子节点个数
- // 二叉树叶子节点个数
- int BinaryTreeLeafSize(BTNode* root) {
- if (root == NULL)
- return 0;
- if (root->left == NULL && root->right == NULL)
- return 1;
- return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
- }
递归子问题:左右子树的叶子节点数的和
返回条件:当节点为空时和左右子树同时为空

3.4 二叉树第k层节点个数
- int BinaryTreeLevelKSize(BTNode* root, int k) {
- if (root == NULL)
- return 0;
- if (k == 1)
- return 1;
- return BinaryTreeLevelKSize(root->left, k - 1)+BinaryTreeLevelKSize(root->right, k - 1);
- }
递归子问题:在k-1层左右子树的节点
返回条件:当节点为空时和k等于1

3.5 二叉树查找值为x的节点
- // 二叉树查找值为x的节点
- BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {
- if (root == NULL)
- return NULL;
- if (root->val == x)
- return root;
- //如果找到了直接返回
- BTNode* ret1 = BinaryTreeFind(root->left, x);
- if (ret1)
- return ret1;
- BTNode* ret2 = BinaryTreeFind(root->right, x);
- if (ret2)
- return ret2;
- }
递归子问题:在左和右子树分别寻找
返回条件:当节点为空时和当节点找到
四、二叉树的创建和销毁
我们之前是通过手动来创建一个二叉树的,现在我们来实现二叉树真正的创建。
4.1 二叉树的创建
通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树,其中#代表节点为空- //其中a[]="abc##de#g##f###",pi为下标
- BTNode* BinaryTreeCreate(BTDataType* a, int* pi){
- if(a[*pi]=='#')
- {
- (*pi)++;
- return NULL;
- }
- BTNode* root=(BTNode*)malloc(sizeof(BTNode));
- root->val=a[(*pi)++];
- //创建左子树
- root->left=BinaryTreeCreate(a,pi);
- //创建右子树
- root->right=BinaryTreeCreate(a,pi);
- return root;
- }
这里的递归子问题为:分别创建左右子树
返回条件:当遇到#即返回
4.2 二叉树的销毁
- // 二叉树销毁
- void BinaryTreeDestory(BTNode** root) {
- if (root == NULL)
- return;
- //分别销毁节点的左右子树
- BinaryTreeDestory(&(*root)->left);
- BinaryTreeDestory(&(*root)->right);
- free(*root);
- *root = NULL;
- }
我们这里使用二级指针来销毁二叉树,也可以用一级指针,只不过需要在函数外面将根节点手动置空。
4.3 是否为完全二叉树
- //是否为完全二叉树
- bool BinaryTreeComplete(BTNode* root) {
- Queue pq;
- QueueInit(&pq);
- if (root != NULL)
- QueuePush(&pq, root);
- while (!QueueEmpty(&pq))
- {
- BTNode* foront = QueueFront(&pq);
- QueuePop(&pq);
- if (foront == NULL)
- break;
- QueuePush(&pq, foront->left);
- QueuePush(&pq, foront->right);
- }
- while (!QueueEmpty(&pq))
- {
- BTNode* foront = QueueFront(&pq);
- QueuePop(&pq);
- if (foront != NULL)
- return false;
- }
- return true;
- QueueDestroy(&pq);
- }
我们运用层序遍历来解决这个问题,只要遇到空结点,判断后面节点是否为空,只要有一个不为空,就不是完全二叉树。
总结
以上文章,我们讲了二叉树的链式结构的遍历和实现,希望对你有所帮助。
-
相关阅读:
SSM整合流程
NEFU离散数学实验2-容斥原理
PMP考生必读,7月30日考试防疫要求都在这里
C语言从入门到入土——函数
重学SpringBoot3-集成FreeMarker
阻塞队列BlockingQueue
基于深度学习的车道检测(一)
GD32F103 硬件 IIC
CentOS7中安装VMwareTools(非图形界面)
Java保留关键字简介说明
- 原文地址:https://blog.csdn.net/2301_76613753/article/details/138136864
