slam数学补充

协方差矩阵的计算

M=(p̃ − μ)(p̃ − μ) T / (n+1)
μ = Σ p̃ / (n+1)

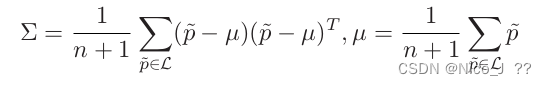
协方差矩阵的意义 以及 特征向量和特征值的关系

从数据表面看：
当M(n,n)过大意味着在数据均值的n维上变化较大，反之M(n,n)过小意味着数据在均值 的n维上变化不大。
当M(n,m)过大意味着数据在均值的n和m维上变化较大，数据在m和n轴的相关性较强。
反之M(n,m)过小意味着数据在均值的n和m维上变化较小，数据在m和n轴的相关性较弱。
从特征向量和特征值看：
M * n = a * n (其中M为协方差矩阵吗,n为特征向量,a为特征值)
不知道如何表达，有点抽象
协方差矩阵的特征向量意义：样本在均值处拟合(投影？)的直线
协方差矩阵的特征值意义：表示样本拟合直线的程度，越大意味着样本越偏离于特征向量，特征值为1时拟合最好
从迹和行列式看：
迹：所有样本的每个维度和均值的差值平方和
行列式：越大误差越大