继去年上半年一鼓作气研究了几种不同的模版匹配算法后,这个方面的工作基本停滞了有七八个月没有去碰了,因为感觉已经遇到了瓶颈,无论是速度还是效率方面,以当时的理解感觉都到了顶了。年初,公司业务惨淡,也无心向佛,总要找点事情做一做,充实下自己,这里选择了前期一直想继续研究的基于离散夹角余弦相似度指标的形状匹配优化。
在前序的一些列文章里,我们也描述了我从linemod模型里抽取的一种相似度指标用于形状匹配,个人取名为离散夹角余弦,其核心是将传统的基于梯度点积相似度的的指标进行了离散化:
传统的梯度点积计算公式如下:
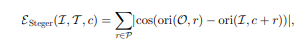
对于任意的两个点,通过各自的梯度方向,按照上述公式可计算出他们的相似度。
那么离散夹角余弦的区别是,不直接计算两个梯度方向的余弦,而是提前进行一些定点化,比如,早期的linemod就是把360度角分为了8份,每份45度,这样[0,45]的梯度方向标记为0,[45,90]的梯度方向标记为1,依次类推,直到[315, 360]之间的梯度方向标记为7,这样共有8个标记,然后提前构建好8个标记之间的一个得分表,比如,下面这样的一个表:

这个表的意思也很简单,就是描述不同标记之间的得分,比如两个点的梯度方向,都为3或者4或者5,那么他们的得分就比较高,可以取8,如果一个为1,一个为6,则得分就只有2, 一个为0,一个为5,则得分为0(即完全相反的两个方向)。
很明显,角度量化的越细,则得到的结果越和传统的梯度点积结果越接近。但是计算量可能也就越大,
关于这个过程,我去年的版本也有弄过8角度、16角度及32角度,个人觉得,在目前的计算机框架下,16角度应该是既能满足进度要求,又能在速度方面更为完美的一个选择。
这里记录下最近对基于16角度离散余弦夹角指标的形状匹配的进一步优化过程。
一、核心的优化策略
通过前面的描述,我们知道,这种方法的得分是通过查表获取的,而且,在大部分的计算中,是没有涉及到浮点计算的,我们通过适当的构造表的内容,可以通过简单的整数类型的加减乘除来得到最后的得分。这个的好处有很多,其中一个就是精度问题,在基于梯度点积的计算中,如果采用float类型来累计计算结果,通常或多或少的存在某些情况下的精度丢失,而且还不好定位哪里有问题。还有个好处就是真的可以加速,当然这个的加速主要是通过一个很特殊,但是又很有效的SSE指令集语句实现的,这个指令就是_mm_shuffle_epi8,其原型及相关介绍如下:
__m128i _mm_shuffle_epi8 (__m128i a, __m128i b)
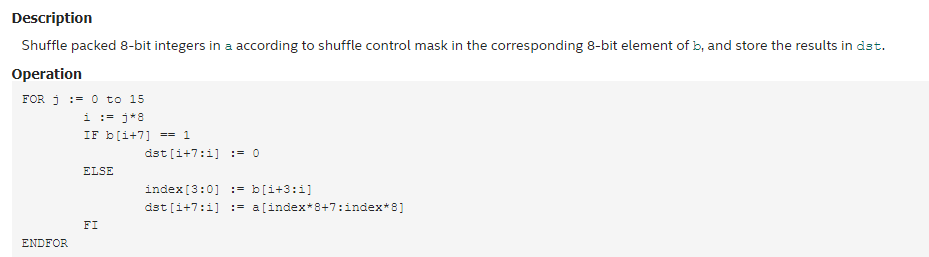
这是个很牛逼的东西,如果我们把a看成一个16个元素的字节数组,b也是一个16个元素的字节数据,则简单的理解他就是实现下述功能:
dst[i] = a[b[i]]; 即一个16个元素的查表功能。
很明显,b[i]要在0到15之间才有效,否则,就查不到元素了,但是该指令还有比较隐藏的功能是,当b[i]大于15时,dst就返回0了。
为什么说这个指令牛逼,我们看我们前面说的这个获取离散夹角余弦的过程,对于两个等面积的区域,假定一个区域的量化后的离散角度标记保存在QuantizedAngleT内存中,另外一个保存在QuantizedAngle内存中,他们的宽和高分别为ValidW和ValidH,则这两个区域按照前面定义的标准,其得分可用下述代码表示(这里SimilarityLut是16角度离散的):
int Score = 0; for (int Y = 0; Y < ValidH; Y++) { int Index = Y * ValidW; for (int X = 0; X < ValidW; X++) { Score += SimilarityLut[QuantizedAngleT[Index + X] * 16 + QuantizedAngle[Index + X]]; // Score += SimilarityLut[QuantizedAngleT[Index + X], QuantizedAngle[Index + X]]; } }
如果把SimilarityLut看成是二维的数组,上面注释掉的得分可能看起来更为清晰。
实际上,我们在进行模版匹配的时候大部分都是在进行这样的得分计算,因此,如果上面的过程能够提速,那么整体将提速很多。
通常,查表的算法是无法进行指令集优化的(AVX2的gather虽然有一定效果,但是弄的不好会适得其反),但是,正是因为我们本例的特殊性,使得这个查表反而更有利于算法的性能提高。
注意到前面有说过我们在进行16角度量化时,量化的标记范围是[0,15],意味着什么,这个正好是_mm_shuffle_epi8 指令里参数b的有效范围啊。
但是仔细看上面的SimilarityLut表,他由两个变量确定索引,这就有点麻烦了,解决的办法是换位思考,我们能不能固定其中的一个呢,这个就要结合我们的实际应用了。
在形状匹配中,我们提取了很多特征点,然后需要使用这些特征点对图像中有效区域范围的目标进行得分统计,也就是说任何一个位置,都要计算所有特征点的得分,并计总和,一个简单的表示为:
for (int Y = 0; Y < ValidH; Y++) { int Index = Y * ValidW; for (int X = 0; X < ValidW; X++) { int b = 图像位置对应的量化值 for (int Z = 0; Z < Template.PointAmount; Z++) { int a = 模版位置对应的量化值 Score += SimilarityLut16[a, b]; } } }
这种情况a,b在每次独立的小循环中还是变化的,一样无法使用指令集。
不过,如果我们调换下循环的顺序,改为以下方式:
for (int Z = 0; Z < Template.PointAmount; Z++) { int a = 模版位置对应的量化值 for (int Y = 0; Y < ValidH; Y++) { int Index = Y * ValidW; for (int X = 0; X < ValidW; X++) { int b = 图像位置对应的量化值 Score += SimilarityLut16[a, b]; } } }
此时,a在内部循环里是不变的,我们通过a之可以定位到SimilarityLut16的a*16地址处,并加载16字节内容,作为查找表的内容,而b值也可以一次性加载16个字节,作为查找的索引,这样一次性就能获得16个位置的得分了。
还有一点,我们在算法里有个最小对比度的东西, 这个东西是用来加快速度的,即梯度值小于这个数据,我们不要这个点参与到匹配中,即此时这个点的得分是0,为了标记这样的点,我们需要再原图的量化值里增加不在[0,15]范围内的东西,一旦有这个东西存在,我们的普通C代码里就需要添加类似这样的代码了:
if (QuantizedAngle[Index + X] != 255) Score += SimilarityLut[QuantizedAngleT[Index + X] * 16 + QuantizedAngle[Index + X]];
这里我使用了255这个不在[0,15]范围内的数字来表示这个点不需要参与匹配计算。本来说,如果刚刚那条_mm_shuffle_epi8指令,只是纯粹的实现[0,15]索引之间的查表,那有了这个东西,这个指令又就没法用了,但是恰恰这个指令能实现在索引不在0到15之间,可以返回其他值,而这个其他值恰好又是0,你们说是多么的巧合和神奇啊。所以,这一切都是为这个指令准备的。我们看看其他shuffle指令,包括_mm_shuffle_epi32,_mm_shuffle_ps,都没有这个附带的功能。
其实这里还是要交代一点,这个算法,如果遇到那种不能用指令集的机器,或者说用纯C语言去实现,效率就比较低了,因为C语言里只能直接查表,而且还要有那个判断。
二、特征点数量的展开即贪婪度参数的舍弃
linemod里使用8角度的特征,其两个特征之间的得分最大值为8,其内部使用了16位的加法,所以其最大的特征点数量为8096个,当模型较大时,往往会超出这个数量的特征点,特别是在最后面基层金字塔的时候,一种方案就是我们限制特征点的数量,并对特征点进行合适的提取,这也不失为一种方案。 那想要完美呢,就必须还得是上32位的加法。这里就存在一个问题,精度和速度如何同时保证,毕竟在SSE指令集的世界里,16位的加法是要比32位的加法快的。
一种解决方案就是,对特征点进行分区,我们按照可能超出16位能表达的最大范围时特征点的数量为区间大小,对特征点按顺序进行多区间划分,在每个小区间里还是用16位的指令集加法,完成一次后,把临时结果在加到32位的数据里。这样就精度和速度都能兼顾了,只不过代码又复杂了一些。
当我们尝试了这么多努力后,我们发现无论是顶层的得分计算,还是后续的每层的局部更新,其速度都变得飞快,这个时候我们又想到了一个贪婪度参数,这个东西,在论文有提到,可以提前结束循环,加快速度。可是,我也想尝试把这个东西加入到我这个算法的过程里,我发现他会破坏我整体的节奏,最终我们选择舍弃了这个参数,核心理由如下:
1、提前结束循环,是需要进行判断的,而且是每次都要判断,特别是对于后期的局部更新判断,因为大部分候选点都是能满足最小得分要求的,这部分的判断一般来说,基本上就无法满足了,也就是纯粹的多了这些无效判断。
2、因为我们使用了_mm_shuffle_epi8指令,一次性可以处理16个位置的得分,也就是这个粒度是16个像素,而如果使用SSE进行判断,也只有当16个位置都不满足最小得分要求后,才可以跳出循环,这个在很多情况下也是得不偿失的。
三、目标只有部分在图像内的识别
有些情况下,被识别的目标只有局部在图像范围内,而我们也期望能识别他,这个功能,我知道早期版本的halcon是没有的,他只能识别那些特征点完全在图像内的目标(不是模版图像边缘)。我早期版本也么有这个功能,后期有做过一些扩展,扩展的方法是通过扩大原始图像合适的范围,同时为了避免不增加新的边缘信息,扩展的部分都是用了边界的像素值。这样做在大部分情况下是能够解决问题的,不过其实也隐藏的一些不合理的地方,这些扩展的部分在细节上还是会产生额外的边缘的,只是不怎么明显。因此,这个版本,我也考虑了几个优化,在内部直接实现了边缘的扩展。
这里有几个技巧。
1、原图的金字塔图像还是不动。
2、计算原图每层金字塔图像的角度量化值时,对这个量化值进行扩展,扩展的部分的量化值填充前面说的那个不在[0,15]之间的无效值,比如这里是255,这样,这些区域的得分就是0。
3、为了能保证在极端情况下这些部分在图像的目标能被识别,扩展的大小要以特征有效值的外接矩形的对角线长度为基准,再进行适当的扩展(这个扩展也有特别要求)。
4、计算完成后,坐标值要进行相应的调整。
通过这种方式,可在内部实现缺失目标的识别,而且在内存占用、速度等方面也有一定的优势。
四、最小外接矩形识别重叠
halcon有说过其maxoverlap参数是通过计算特征点的最小外接矩形之间的重叠来实现的,在我以前的版本中,这个功能是通过其他的简易方法来搞定的。这个主要是以前搞不定最小外接矩形的计算,年初,恰好从opencv里翻译可扣取了一些代码,起重工就有最小外接矩形的获取,这个需要通过计算凸包以前其他一些复杂的东西搞定,我没有看懂原理,只是直接扣取了代码,不过CV的代码绕来绕去,扣的我也是头晕脑胀,总算搞出来了。
那么这里其实也有蛮多的细节和可选方案,我列举如下:
1、在创建特征时,计算好每个旋转后的特征的最小外接矩形(勾选了预生成模型数据)。
2、在最后确定的底层金字塔里所有的候选点出计算每个特征点对应的外接矩形。
3、只计算底层金字塔0角度是特征单的最小外接矩形,然后其他底层金字塔的最小外接矩形用他旋转得到。
我们实际考虑啊,方案一对创建模型不友好,方案二实际测试对运行的效率产生了不良影响,方案3最好,基本不耗时,而且对精度的影响也非常有限,所以可以选择方案3。
五、其他的一些我未公开的讨论的课题
1、16角度SimilarityLut的值如何设计,其实在halcon里有个metric参数,他有三种选择,使用极性、忽略全局极性、忽略局部极性。如果想前面给出的那种8角度的SimilarityLut,是只能实现使用极性和忽略全局极性的。这里适当扩展,就可以实现三个都有了,而且对是速度提升还有好处。
2、5*5局部得分过程的特别优化,尤其是如何高效的加载每行5个字节,并拼接成合适的形式,使得能快速的使用指令集。
3、也可以使用8*8的局部区域(非对称的局部更新),这样方便使用指令集,但是因为数量变大,还是没有优化后的5*5快。
4、在最顶层,计算候选点时,可以直接计算,也可以考虑使用ResponseMaps,其中,测试表明还是使用ResponseMaps快一点。
5、还是候选点的选择问题,在最顶层,目前我还是用的某个角度下的二维得分结果中选择得分大于最小得分要求,同时是5*5领域的最大值作为候选点,这种方式留下的候选点还是有很多的,对于只有旋转的匹配,是否可以考虑在3D(X方向、Y方向以及角度方向)的空间里,选得分大于最小得分要求且是5*5*5领域的最大值呢,这样候选点肯定会少很多,但是代码的编写似乎变得困难了很多,还有占用内存问题。那如果扩展到多尺度的匹配,或者是各项异性的匹配,那就要在4D和5D空间搜索最大值了,这个感觉就更为复杂了。
6、另外,再有顶层金字塔向下层金字塔迭代更新的过程中的候选点的舍弃问题,也值得探讨,到底是只根据得分是否满足需求,还是根据一些物理空间或者角度方面的特性做些特别的优化和舍弃呢,而且这种舍弃行为本身有的时候可能会带来性能的下降,因为在搜索那些目标可以舍弃时,需要一个循环,当候选目标有几千个的时候,两重这样的循环会对对后续候选点变少带来的性能加速起到反向作用,这个甚至会超过候选点变少带来的加速。所以 目前我这个版本为了稳定性,只是对得到的重复的点做了舍弃。
7、原本再想一个优化,即我们的特征点的保存顺序问题,现在只有0角度的特征点的保存顺序是X及Y方向都是由小向大方向坐标排列,这样访问的时候和图像的内存布局方向性一致,按理说cache miss要小一些。但是,如果按照顺序把0角度的特征点旋转后,得到新的位置信息,一般来说肯定不是按照这样的顺序排列的了,所以访问时随机性就差了一些,那是否我再计算前把这些点再按0角度时那样做个排序后,有利于算法的性能呢,我做了实际的测试,应该说基本没啥区别吧。
六、结论
综合以上各种优化手段后,目前经过测试,速度较以前有很大的提高,而且和基于传统的梯度点积的方法比较,速度更具有优势,而且精度也不逞多让。我们测试在2500*2000的灰度中查找 300 * 150的多目标,大约耗时11ms, 传统的方式结合贪婪度耗时也需要18ms。这个时间我测试和halcon的比较已经非常接近了。当然这种比较还是要看具体的测试图。
从算法精度上看,怎么上定位也是很准确的,在执行过程中,占用的内存也不大,因此,个人觉得这个方法不失为一个优质的算子。

如果想时刻关注本人的最新文章,也可关注公众号或者添加本人微信: laviewpbt

