Leetcode 104. 二叉树的最大深度

题目描述：
给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

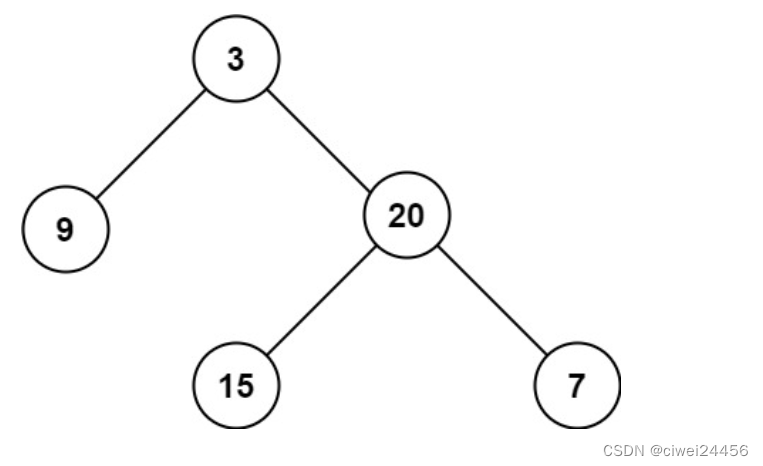
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：
输入：root = [1,null,2]
输出：2

思路：
解法1：后序遍历+递归
此树的深度和其左（右）子树的深度之间的关系。显然，此树的深度 等于 左子树的深度 与 右子树的深度中的 最大值 +1。

步骤：
1、终止条件： 当 root​ 为空，说明已越过叶节点，因此返回 深度 0 。
2、递推： 本质上是对树做后序遍历。
计算节点 root​ 的 左子树的深度 ，即调用 maxDepth(root.left)。
计算节点 root​ 的 右子树的深度 ，即调用 maxDepth(root.right)。
3、返回值： 返回 此树的深度 ，即 max(maxDepth(root.left), maxDepth(root.right)) + 1。

python：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        return max(self.maxDepth(root.left),self.maxDepth(root.right))+1
1
2
3
4
5
6
7
8
9
10
11

复杂度分析：
时间复杂度 O(N)： N为树的节点数量，计算树的深度需要遍历所有节点。
空间复杂度 O(N)： 最差情况下（当树退化为链表时），递归深度可达到 N。

解法2：层序遍历+队列
树的层序遍历 / 广度优先搜索往往利用 队列 实现。
每遍历一层，则计数器 +1+1+1 ，直到遍历完成，则可得到树的深度。

步骤：
1、当 root​ 为空，直接返回 深度 000 。
2、初始化： 队列 queue （加入根节点 root ），计数器 res = 0。
3、循环遍历： 当 queue 为空时跳出。
初始化一个空列表 tmp ，用于临时存储下一层节点。
遍历队列： 遍历 queue 中的各节点 node ，并将其左子节点和右子节点加入 tmp。
更新队列： 执行 queue = tmp ，将下一层节点赋值给 queue。
统计层数： 执行 res += 1 ，代表层数加 111。
4、返回值： 返回 res 即可。

python：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0

        queue,res=[root],0
        while queue:
            tmp=[]
            for node in queue:
                if node.left:
                    tmp.append(node.left)
                if node.right:
                    tmp.append(node.right)

            queue=tmp
            res+=1   
        return res
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

复杂度分析：
时间复杂度 O(N) ： N 为树的节点数量，计算树的深度需要遍历所有节点。
空间复杂度 O(N) ： 最差情况下（当树平衡时），队列 queue 同时存储 N/2个节点。