基于遗传算法GA的机器人栅格地图最短路径规划，可以自定义地图及起始点（提供MATLAB代码）

一、原理介绍

遗传算法是一种基于生物进化原理的优化算法，常用于求解复杂问题。在机器人栅格地图最短路径规划中，遗传算法可以用来寻找最优路径。

遗传算法的求解过程包括以下几个步骤：

1. 初始化种群：随机生成一组初始解，每个解表示机器人在栅格地图上的路径。

2. 评估适应度：根据路径的长度或者其他评价指标，计算每个解的适应度值。

3. 选择操作：根据适应度值，选择一部分优秀的解作为父代，用于产生下一代解。

4. 交叉操作：通过交叉操作，将父代解的某些部分进行交换和组合，生成新的解。

5. 变异操作：对新生成的解进行变异操作，引入一定的随机性，增加解的多样性。

6. 更新种群：将新生成的解加入到种群中，并淘汰一部分适应度较低的解。

7. 终止条件判断：根据预设的终止条件（如达到最大迭代次数或找到满意的解），判断是否结束算法。

8. 输出结果：输出最优解作为机器人在栅格地图上的最短路径。

二、部分代码

close all;
clear;
clc;
% 输入数据,即栅格地图.20行20列
Grid=  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
     0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
     0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0;
     0 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 1 0 0 0;
     0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 1 1 0 0;
     0 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0;
     0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
     0 0 0 0 0 0 1 1 1 0 1 0 1 1 0 0 1 1 1 0;
     0 1 1 1 0 0 0 0 0 0 1 0 1 1 0 0 0 0 1 0;
     0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0;
     0 0 0 0 0 0 0 1 1 0 1 1 1 1 0 0 0 0 1 0;
     0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0;
     0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0;
     0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0;
     0 0 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0;
     0 0 1 1 0 0 1 1 1 0 1 0 0 0 0 0 0 0 1 0;
     0 0 0 0 0 0 1 1 1 0 1 0 0 0 1 0 0 1 1 0; 
     0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0;
     0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0;
     0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0];
start_num = 18;    % 起点编号
end_num = 380;    % 终点序号
NP = 300;       % 种群数量
max_gen = 300;  % 最大进化代数
pc = 0.8;      % 交叉概率
pm = 0.2;      % 变异概率
a = 1;         % 路径长度比重
b = 8;         % 路径顺滑度比重
z = 1;         
new_pop1 = {}; % 元胞数组，存放路径
[y, x] = size(Grid);
% 起点所在列（从左到右编号1.2.3...）
start_column = mod(start_num, x) + 1; 
% 起点所在行（从上到下编号行1.2.3...）
start_row = fix(start_num / x) + 1;  %Y = fix(X) 将 X 的每个元素朝零方向四舍五入为最近的整数
% 终点所在列、行
end_column = mod(end_num, x) + 1;
end_row = fix(end_num / x) + 1;

三、部分结果

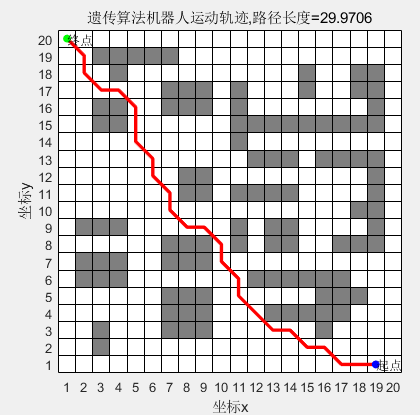
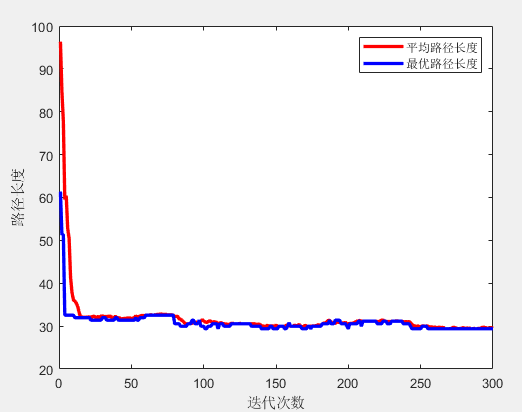
四、完整MATLAB代码

点击main.m即可运行，可以自定义地图及起始点。