算法训练day41Leetcode343. 整数拆分 96.不同的二叉搜索树

343.整数拆分

题目描述

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

示例 1:

输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

提示:

• 2 <= n <= 58

题目分析

因为拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的。

例如 6 拆成 3 * 3， 10 拆成 3 * 3 * 4。 100的话 也是拆成m个近似数组的子数 相乘才是最大的。

只不过我们不知道m究竟是多少而已，但可以明确的是m一定大于等于2，既然m大于等于2，也就是 最差也应该是拆成两个相同的 可能是最大值。

acm模式代码

#include 
#include 
#include 
 
 
class Solution {
public:
    int integerBreak(int n) {
        //定义dp数组
        std::vector<int> dp(n+1, 0);
        //确定初始值
        dp[0] = 0;
        dp[1] = 0;
        dp[2] = 1;
        for (int i = 3; i < dp.size(); i++) {
            for (int j = 0; j < i; j++) {
                //递推公式
                dp[i] = std::max((j*(i-j)), std::max(j * dp[i - j],dp[i]));
            }
        }
            //打印dp数组
        // for (int i:dp) {
        //     std::cout << i << " " ;
        // }
        return dp[n];
    }
 
};
 
int main() {
    Solution sol;
    int n = 10;
    int max = sol.integerBreak(n);
    std::cout << "max:" << max << std::endl;
    return 0;
}

96.不同的二叉搜索树

题目描述 

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

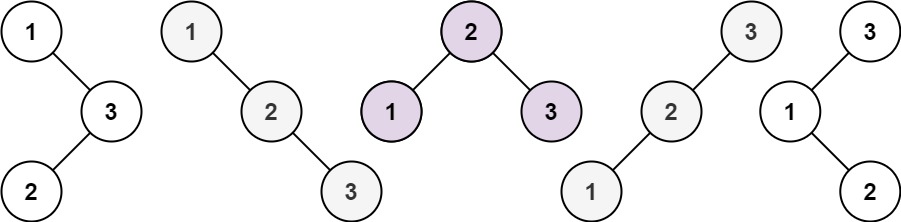
输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

提示：

• 1 <= n <= 19

题目分析

二叉搜索树（Binary Search Tree，简称BST），是一种具有特定属性的二叉树数据结构。它的每个节点都具有以下性质：

1. 节点的值大于左子树上任意节点的值：这意味着所有在左子树中的值都小于当前节点的值。
2. 节点的值小于右子树上任意节点的值：这意味着所有在右子树中的值都大于当前节点的值。
3. 左右子树也分别为二叉搜索树：不仅当前节点需要满足上述两个条件，其左右子树的每个节点也都必须满足同样的条件。

dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量

元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量

元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量

元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

acm模式代码

#include 
#include 
 
class Solution {
public:
    int numTrees(int n) {
        std::vector<int> dp(n+1, 0);
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                //ditui
                dp[i] += dp[j - 1]* dp[i - j];
            }
        }
        // 打印dp
        // for (int i: dp) {
        //     std::cout << i << " ";
        // }
        return dp[n];
    }
};
 
int main() {
    int n = 3;
    Solution sol;
    int sum = sol.numTrees(n);
    std::cout << "sum: " << sum << std::endl;
    return 0;
}