OFDM系统各种调制阶数的QAM误码率（Symbol Error Rate）与 误比特率（Bit Error Rate）仿真结果

本文是OFDM系统的不同QAM调制阶数的误码率与误比特率仿真，仅考虑在高斯白噪声信道下的情景，着重分析不同信噪比下的误码（符号）率性能曲线，不关心具体的调制与解调方案，仿真结果与理论的误码率曲线进行了对比。

考虑一个简单的OFDM系统，每个频域子载波承载一个QAM调制符号，在经过不同信噪比白噪声信道之后，每个QAM调制符号的解调性能如何，每个符号对应的比特解码性能如何？理论的误码性能如何？

代码

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120

clc;close all;clear   %% Seting parameters EbN0_list = 0:1:10; Q_order_list = 2:2:10; loopNumber = 10; fprintf('Qm\t EbN0 \t \t EsN0 \t \t SNR_Cal \t \t ser \t\t ser_theory\t\t\t ber\t\t nloop \t\t \n'); for iQorder = 1 : length(Q_order_list) for iEbN0 = 1 : length(EbN0_list)   %% Frame structure N_Frame = 10; N_Symbol = 14; N_RB = 106; N_SC_perRB = 12; N_SC = N_RB * N_SC_perRB; N_Ant = 1; N_fft_order = floor(log2(N_RB * N_SC_perRB)); N_fft = 2^(N_fft_order+1); N_cp = N_fft/8; EbN0 = EbN0_list(iEbN0);   %% Modulation Q_order = Q_order_list(iQorder); Qm = 2^Q_order; N_bit = N_Frame * N_Symbol * N_RB * N_SC_perRB * Q_order;   %% Noise Calculation SNR =  EbN0 + 10 * log10(Q_order);   %% Loop for iloop = 1 :loopNumber data_bit_in = randi([0 1], 1, N_bit); dataSymbolsIn = bi2de(reshape(data_bit_in, Q_order, N_bit/Q_order).', 'left-msb'); dataMod = qammod(dataSymbolsIn, Qm,'UnitAveragePower', true);   %% Show Constellation %scatterplotme(dataMod)   %% Resource Mapping RE_Grid = zeros(N_RB * N_SC_perRB,N_Symbol * N_Frame); dataMod_tmp = reshape(dataMod,N_RB * N_SC_perRB,[]); %only data Power_Scale = 1; RE_Grid_all = Power_Scale * dataMod_tmp;   %% IFFT add CP frame_mod_shift = ifftshift(RE_Grid_all); ifft_data = ifft(frame_mod_shift,N_fft)*sqrt(N_fft); %ifft_data = ifft(frame_mod_shift)*sqrt(1272); Tx_cd = [ifft_data(N_fft-N_cp+1:end,:);ifft_data]; time_signal = reshape(Tx_cd,[],1);   %% Channel power_RE = sum(sum(abs(RE_Grid_all).^2)) / N_RB / N_SC_perRB / N_Symbol / N_Frame; power_tp = sum(sum(abs(ifft_data).^2)) / N_RB / N_SC_perRB / N_Symbol / N_Frame;  %IFFT zero padding averages the true RE Power N0 = power_RE .* 10.^(-SNR / 10); white_noise_starand = 1/sqrt(2)*(randn(size(time_signal)) + 1j * randn(size(time_signal))); TransmittedSignal = time_signal + sqrt(N0) * white_noise_starand;   %% Receive and Sys ReceivedSignal = TransmittedSignal;   %% FFT and Frame   frame_recieved_parallel = reshape(ReceivedSignal, N_fft + N_cp, []); frame_Received = frame_recieved_parallel(N_cp + 1:end,:);    frame_Grid_Received = fft(frame_Received,N_fft) / sqrt(N_fft); RE_Grid_all_Received = fftshift(frame_Grid_Received(1 : N_SC,:));   %% Demodulation RE_PreDeMod = reshape(RE_Grid_all_Received,[],1); dataSymbolsOut = qamdemod(RE_PreDeMod, Qm,'UnitAveragePower', true); data_bit_out = reshape((de2bi(dataSymbolsOut, 'left-msb')).',1,[]); power_RE_receid = sum(sum(abs(RE_PreDeMod).^2)) / N_RB / N_SC_perRB / N_Symbol / N_Frame; snr_all(iQorder,iEbN0,iloop) = 10*log10(power_RE/(power_RE_receid - power_RE)); %% Result: Ser and Ber %Ser sym_err = length(find(dataSymbolsOut - dataSymbolsIn)); ser_all(iQorder,iEbN0,iloop) = sym_err / length(dataSymbolsOut); %Ber bit_error = sum(abs(data_bit_out - data_bit_in)); ber_all(iQorder,iEbN0,iloop) = bit_error / length(data_bit_out); end sers = mean(ser_all,3); snrs = mean(snr_all,3); bers = mean(ber_all,3); sers_theory(iQorder,iEbN0) = QAM_SER_Theory(Qm,EbN0);       fprintf('%dQAM\t%f\t %f\t %f\t %e\t\t%e\t\t%e\t\t%d\t\n', Qm, EbN0, SNR,snrs(iQorder,iEbN0),sers(iQorder,iEbN0),sers_theory(iQorder,iEbN0),bers(iQorder,iEbN0),loopNumber);     end end   figure(1) semilogy(EbN0_list, bers(1,:), 'k--+'); hold on grid on semilogy(EbN0_list, bers(2,:), 'r--o'); semilogy(EbN0_list, bers(3,:), 'b--x'); semilogy(EbN0_list, bers(4,:), 'g--s'); xlabel('Eb/N0,dB'); ylabel('BER'); title('BER VERS SNR'); legend('QPSK','16QAM','256QAM','1024QAM');     figure(2) semilogy(EbN0_list, sers(1,:), 'k--+'); hold on grid on semilogy(EbN0_list, sers_theory(1,:), 'k-'); semilogy(EbN0_list, sers(2,:), 'r--o'); semilogy(EbN0_list, sers_theory(2,:), 'r-'); semilogy(EbN0_list, sers(3,:), 'b--x'); semilogy(EbN0_list, sers_theory(3,:), 'b-'); semilogy(EbN0_list, sers(4,:), 'g--s'); semilogy(EbN0_list, sers_theory(4,:), 'g-'); xlabel('Eb/N0,dB'); ylabel('SER'); title('SER VERS SNR'); %SML =  simulation, THR = theory legend('QPSK-SML','QPSK-THR','16QAM-SML','16QAM-THR','256QAM-SML','256QAM-THR','1024QAM-SML','1024QAM-THR');

计算理论误比特率的函数需要参考文献，不过观察误码率与误比特率曲线，大体趋势相同，也许仅相差一个和调制阶数相关的常数（后来验证并非如此简单）。

?

1 2 3 4 5 6 7 8 9 10 11 12 13

%% Theory Symbol Error Rate   function SER = QAM_SER_Theory(Qm,EbN0)    %Reference https://dsplog.com/2012/01/01/symbol-error-rate-16qam-64qam-256qam/    Q_order = log2(Qm);    EsN0_DB =  EbN0 + 10 * log10(Q_order);    EsN0 = 10.^( EsN0_DB/ 10);    k = sqrt(3 / (2*(Qm - 1)));    k_snr = k * sqrt(EsN0);    cer = erfc(k_snr);    SER = 2*(1 - 1/sqrt(Qm))*cer - (1 - 2/sqrt(Qm) + 1/Qm) * (cer.^2); %    cer = erfc(sqrt(EsN0/2)); %    SER = cer - 1/4*cer.^2;

 

 仿真结果

SER VERS SNR（该图理论（THR）误符号率曲线和实际仿真（SML）理论误符号率曲线基本重合）

 

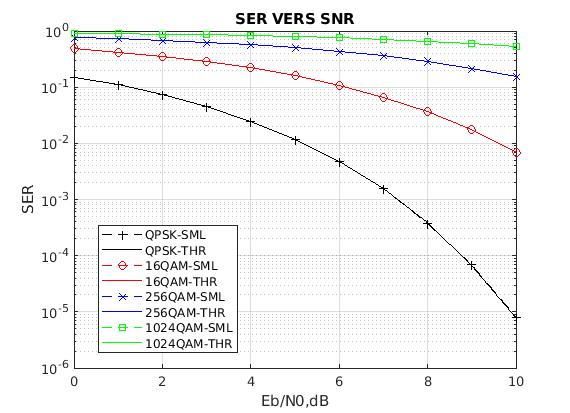
BER VERS SNR（未画出理论误码率曲线）

 

分析结论

本仿真中应该重点关注信噪比的换算，包括Eb/N0(每bit的信噪比)到Es/N0(每QAM符号的信噪比)，频域通过IFFT到时域前后计算SNR，特别是子载波个数与IFFT的点数不相同时，如何在时域加噪声，每个时域采样点的噪声功率N0应该加多大。

反思

1.仅白噪声下的仿真结果，那么在多径信道下的仿真曲线如何呢？如何利用信道均衡来对抗多径带来的频率选择性衰落。
2.在调制阶数越来越高的情况下，误码率与误比特率都随之升高，那么通信中是如何通过调制阶数的升高来提升系统的吞吐量的呢？信道编码的作用。
3.如何利用多个天线MIMO技术来提高通信系统的有效性与可靠性？信道预编码与均衡。