回溯算法01-组合(Java)

1.组合

• 题目描述

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4]]
1
2
3

示例 2：

输入：n = 1, k = 1
输出：[[1]]
1
2

• 题目分析

根据题目可知，本题是求1-n这n个不同的数的组合问题，我们知道对于n个不同的数中的任意k个数组合，当n很大时通过枚举是很难将它枚举完成的，所以我们可以采用回溯算法来解决这一类问题。
1

• 回溯算法的模板

1.确立递归函数及返回值

2.确立回溯的终止条件

3.单层递归逻辑

private void backtracking(参数) {
	//回溯的终止条件
    if (终止条件) {
        存放结果;
        return;
    }
	//回溯算法的遍历过程(集合的大小为树的宽度，递归的深度为树的深度)
    for (选择 ：本层集合的元素) {
        处理节点；
        backtracking(路径， 选择列表);//递归
        回溯，撤销处理的结果
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

1.首先我们确立递归函数及参数(例子：nums=[1,2,3] k = 2)
根据下图递归操作我们可以看出，每次挑选数组nums中的一个元素加入到集合之中：
第一次：集合元素为[1]，剩余元素为[2,3]
第二次：集合元素为[1,2]，剩余元素为[3] 此时集合[1,2]满足k = 2的组合条件，将其存储，因为之后不再再取3会使不满足k个数组合的条件，因此要进行回溯，返回到集合元素为[1]，剩余元素为[2,3]
第三次：集合元素为[1,3],剩余元素为[] 此时要选择元素3加入到集合，因此我们要设置一个索引来避开元素2，这样才不会有重复
...依次回溯，我们发现每次叶子节点为我们想要的结果
 
所以初始化一个回溯函数
void backtrack(int nums[], int startIndex) {
    
}
nums为要组合的元素集合，startIndex为避免每次重复的指针

2.设置终止条件：当我们组合的集合中恰好有k个节点时，表示组合完成
    
3.单层递归逻辑
从startIndex开始，遍历所有可能的元素，将其添加到路径中，并递归调用backtrace方法继续生成下一个元素。完成递归后，需要将最后一个元素从路径中移除，以便尝试其他可能的元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

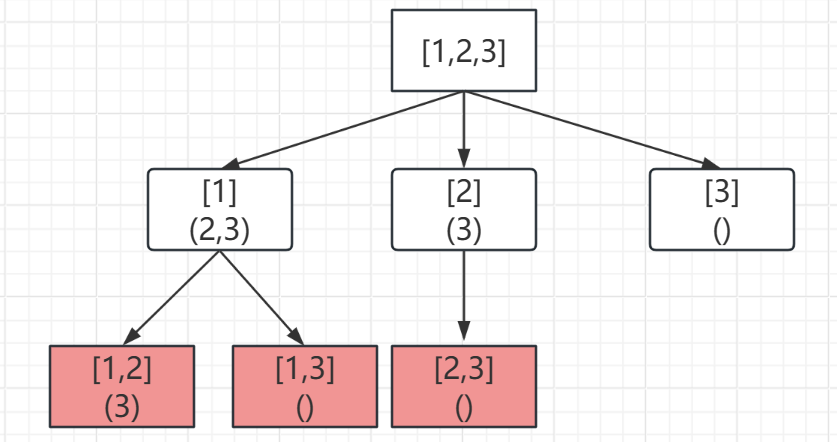
• 以nums=[1,2,3,4] k = 2直观感受一下i与startIndex的变化

i = 1 s = 1 [1]
i = 2 s = 2 [1,2]
//i = 2 s = 2 [1]
i = 3 s = 2 [1,3]
//i = 3 s = 2 [1] 
i = 4 s = 2 [1,4]
//i = 4 s = 2 [1]
i = 2 s = 1 [2]
i = 3 s = 3 [2,3]
//i = 3 s = 3 [2]
i = 4 s = 3 [2,4]
//i = 4 s = 3 [2]
i = 3 s = 1 [3]
...
1
2
3
4
5
6
7
8
9
10
11
12
13
14

• Java代码实现

//list:用于存储一条路径上的元素
    //result：用于返回最后的元素
    LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> result = new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        backtrace(n, k, 1);
        return result;
    }

    //1.确立递归函数的参数及返回值
    //n:树的宽度即求n个数的组合数
    //k：叶子节点即组合个数为k
    //startIndex：用于开始元素遍历的起点
    private void backtrace(int n, int k, int startIndex) {
        //2.确立终止条件
        if (path.size() == k) {//当最后组成的元素集合为k时返回结果
            result.add(new LinkedList<>(path));
            return;
        }
        //3.单层递归逻辑
        for (int i = startIndex; i <= n; i++) {
            path.add(i);
            backtrace(n, k, i + 1);
            path.removeLast();
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26