C++模拟揭秘刘谦魔术，领略数学的魅力

新的一年又开始了，大家新年好呀~。在这我想问大家一个问题，有没有同学看了联欢晚会上刘谦的魔术呢？
这个节目还挺有意思的，它最出彩的不是魔术本身，而是小尼老师“念错咒语”而导致他手里的排没有拼在一起，当时还一度冲上了热搜。

这个魔术的背后其实是一个数学上的问题，它被称为约瑟夫问题，它是一个计算机科学和数学中的问题，在计算机编程的算法中，类似问题又称为约瑟夫环，又称“丢手绢问题”。

它的故事背景是这样的：

据说著名犹太历史学家Josephus（弗拉维奥·约瑟夫斯）有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。问题是，给定了和，一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

在编程上的变形一般是这样的：
N个人围成一圈，从第一个开始报数，第M个出局，第M个出局之后它的下一个又从1开始报数，直到最后剩下一个，其余人都出局。例如N=6，M=5，被杀掉的顺序是：5，4，6，2，3。

给大家模拟一下这个过程：
（第一轮数字5出局，黑色字体的数字 代表n个人，红色字体代表每个人报的数字）

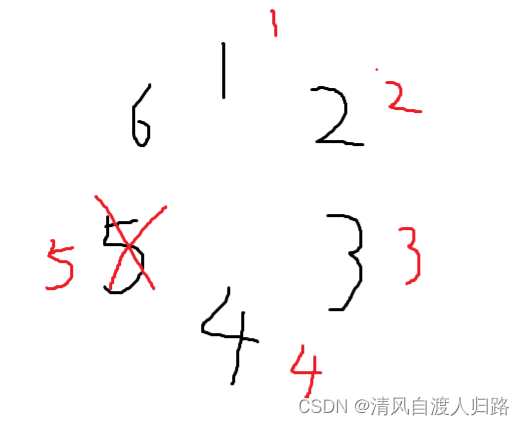
（第一轮数字5出局之后剩下5个数字，从数字6开始从1报数，依次顺下去就是数字4出局）

（第三轮数字依次往后报数，数字6出局）

（第四轮数字2出局）

（第五轮数字3出局，第一个人胜利）

这是约瑟夫环问题的模拟过程，那现在大家一起来看一下程序怎么写。

第一种方法：递归

#include
using namespace std;
int ysf(int n, int k, int i)//本函数是index=0开始
{
	if (i == 1)
		return (n+k-1) % n;
	if (i != 1)
		return (ysf(n - 1, k, i - 1) + k) % n;//即为去掉前面的人构成的新环的第i-1次
}
int main()
{
	int n, k;
	cin >> n >> k;
	for (int i = 1; i <= n; i++)
	{
		cout << ysf(n, k, i)+1 << " ";//加1统一index=1开始
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

第二种：队列

#include
#include
using namespace std;
queue<int> res;
int n, k;
int main()
{
	cin >> n >> k;
	for (int i = 1; i <= n; i++)
	{
		res.push(i);
	}
	int cnt = 0;
	while (!res.empty())
	{
		for (int i = 1; i <= k - 1; i++)//执行k-1次
		{
			res.push(res.front());//将队首元素放队尾去
			res.pop();
		}
		//循环结束后输出队首元素
		cout << res.front() << " ";
		res.pop();//出局
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

第三种：循环链表

#include
#include
using namespace std;
typedef struct node
{
	int data;
	struct node* next;
}Node;
int n, k;
void Joseph_ring(int n, int k)
{
	//开始创建循环链表
	Node* head = NULL, * p = NULL, * r = NULL;//搞三个指针
	head = (Node*)malloc(sizeof(Node));//为head头指针申请一片空间((Node*)为强制类型转换为结构体变量指针）
	head->data = 1;
	head->next = NULL;
	p = head;//创建循环链表用，此时p和head指向头结点
	for (int i = 2; i <= n; i++)//创建剩下的n-1个结点(尾插法顺序插入）
	{
		r = (Node*)malloc(sizeof(Node));
		r->data = i;
		r->next = NULL;
		p->next = r;
		p = r;
	}
	p->next = head;//首尾相接
	p = head;//恢复初始状态
	while (p->next != p)//结束条件是只剩下最后一个（当然用cnt计数也可以）
	{
		for (int i = 1; i < k; i++)
		{
			r = p;//用r保存该删结点的上一个结点
			p = p->next;
		}
		//循环结束后p指针的位置是该删结点的位置
		cout << p->data << " ";
		r->next = p->next;
		p = p->next;
	}
	//whlie循环结束后还剩最后一个结点要输出
	cout << p->data;
}
int main()
{
	cin >> n >> k;
	Joseph_ring(n,k);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

好啦，同学们自己试一试吧~