【C++】十大排序算法之 插入排序 & 希尔排序

本次介绍内容参考自：十大经典排序算法（C++实现） - fengMisaka - 博客园 (cnblogs.com)

排序算法是《数据结构与算法》中最基本的算法之一。

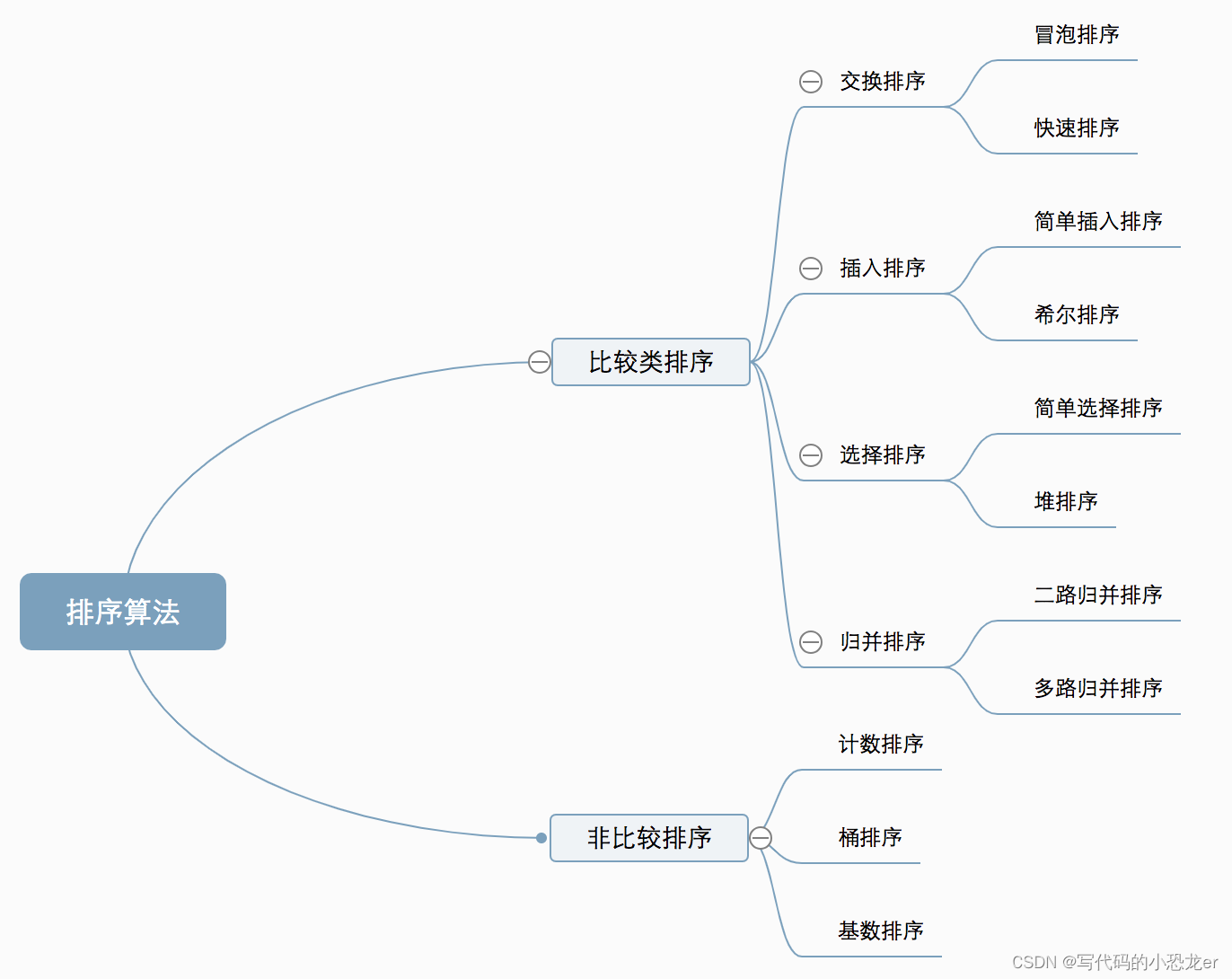
十种常见排序算法可以分为两大类：

• 比较类排序：通过比较来决定元素间的相对次序，时间复杂度为 O(nlogn)～O(n²)。
• 非比较类排序：不通过比较来决定元素间的相对次序，其时间复杂度可以突破 O(nlogn)，以线性时间运行。

【十大经典排序算法分类】

【十大经典排序算法的复杂度分析】

名词解释：

• 时间/空间复杂度：描述一个算法执行时间/占用空间与数据规模的增长关系。

• n：待排序列的个数。

• k：“桶”的个数（上面的三种非比较类排序都是基于“桶”的思想实现的）。

• In-place：原地算法，指的是占用常量内存，不占用额外内存。即空间复杂度为 O(1) 。

• Out-place：非原地算法，占用额外内存。

• 稳定性：假设待排序列中两元素相等，排序前后这两个相等元素的相对位置不变，则认为是稳定的。

---

---

一、插入排序（Insertion-Sort）

        插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

1.1、算法描述

• 将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
• 从头到尾依次扫描未排序序列，将扫描到的每个元素与有序序列的每个元素进行比较，小于哪个有序序列的元素就进行交换，相当于插入到该元素索引位置。

（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

1.2、动图演示

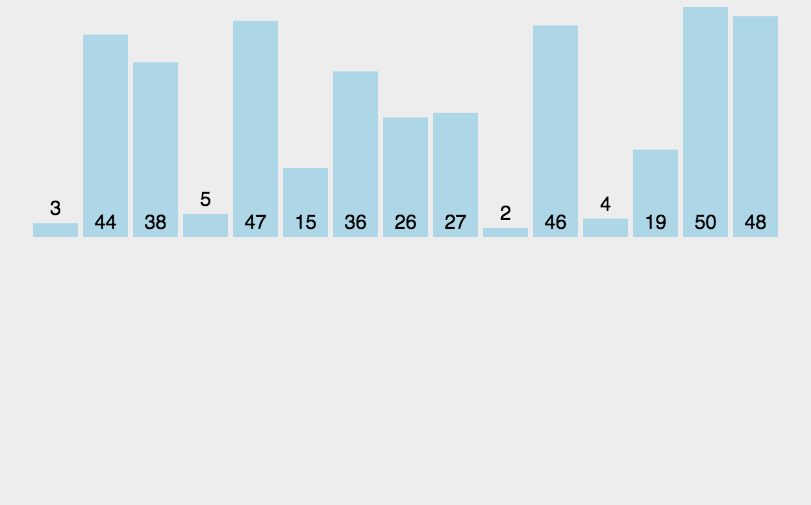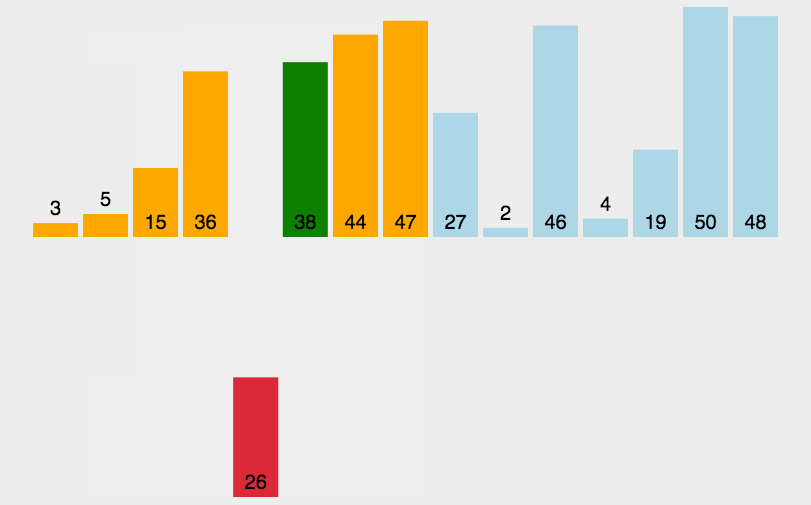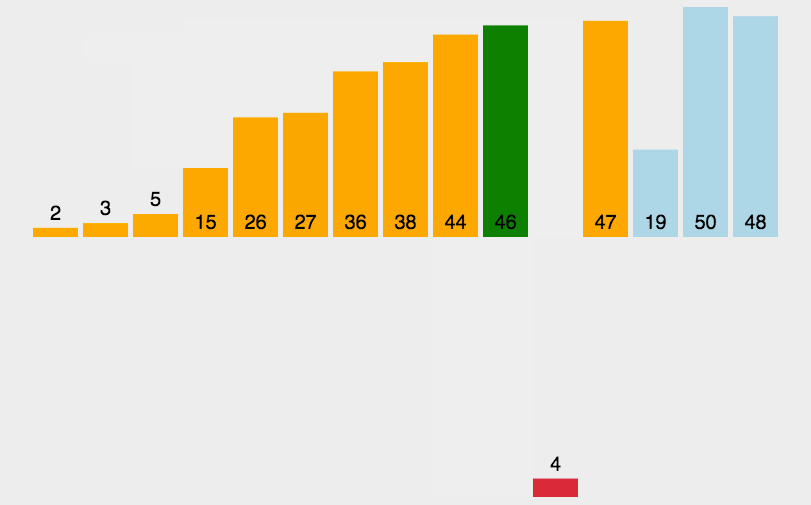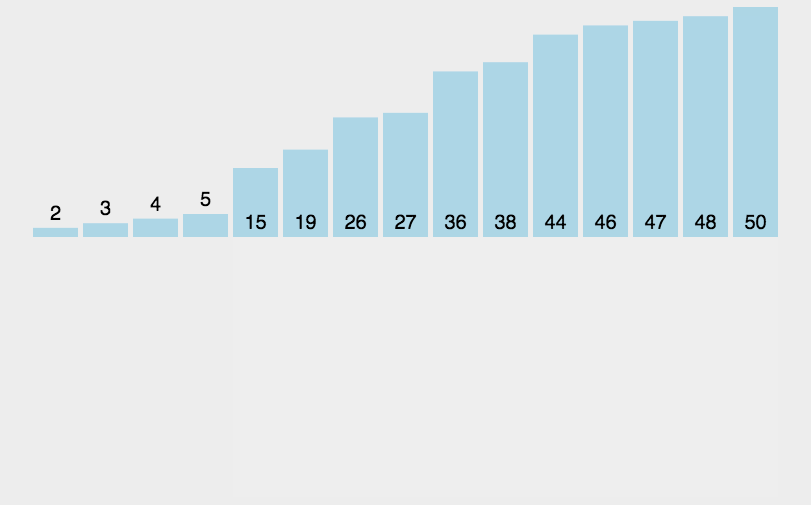
插入排序动图演示

---

1.3、C++编码

/**
* @version Copyright (c) 2024 NCDC, Servo。 Unpublished - All rights reserved
* @file InsertSort.hpp
* @brief 插入排序
* @autor 写代码的小恐龙er
* @date 2024/03/04
*/
 
void InsertSort(int arr[], int n) {
	int i, j, temp;
	for (i = 1; i < n; i++) {
		temp = arr[i];
 
		for (j = i; j > 0 && arr[j - 1] > temp; j--)
			arr[j] = arr[j - 1]; // 把已排序元素逐步向后挪位
 
		arr[j] = temp; // 插入
	}
}

---

1.4 、算法分析

        插入排序在实现上，通常采用 in-place 排序（即只需用到 O(1) 的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

---

---

二、希尔排序（Shell Sort）

        1959年Shell发明，第一个突破 O(n2) 的排序算法，是插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

2.1 、算法描述

        先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：

• 选择一个增量序列 t1，t2，…，tk，其中 ti>tj，tk=1；
• 按增量序列个数 k，对序列进行 k 趟排序；
• 每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

2.2 、动图演示

 选希尔排序动图演示

---

2.3、C++编码

/**
* @version Copyright (c) 2024 NCDC, Servo。 Unpublished - All rights reserved
* @file ShellSort.hpp
* @brief 希尔排序
* @autor 写代码的小恐龙er
* @date 2024/03/04
*/
 
void ShellSort(int *arr[], int size)  
{  
    int i, j, tmp, increment; 
    // 选择一个增量序列 t1，t2，…，tk，其中 ti>tj，tk=1；
    // 按增量序列个数 k，对序列进行 k 趟排序；
    for (increment = size/ 2; increment > 0; increment /= 2) {   
        // 每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，
        // 分别对各子表进行直接插入排序。
        // 仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。
        for (i = increment; i < size; i++) {  
            tmp = arr[i];  
            // 直接插入排序
            for (j = i - increment; j >= 0 && tmp < arr[j]; j -= increment) {  
                arr[j + increment] = arr[j];  
            }  
            // 插入
            arr[j + increment] = tmp;
        }  
    }  
}  

---

2.4 、算法分析

        希尔排序是不稳定排序，所比较快，因为相比冒泡排序，每次交换是跳跃式的。每次排序的时候设置一个基准点，将小于等于基准点的数全部放到基准点的左边，将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换，交换的距离就大的多了。因此总的比较和交换次数就少了，速度自然就提高了。当然在最坏的情况下，仍可能是相邻的两个数进行了交换。因此希尔排序的最差时间复杂度和冒泡排序是一样的都是 O(n²)，它的平均时间复杂度为 O(n log n)。