简单理解注意力机制与实现

在学习注意力机制的过程中，我发现像我这样的麻瓜就不配看论文去理解这个东西。

后面找到了源码，试图从实现看出一些逻辑，发现也不是那么友好。毕竟，麻瓜精通算法也就不是麻瓜了。

万幸，我后来磕磕绊绊的从论文，搜索引擎和源码逐渐的理解他。

论文链接：Attention Is All You Need.pdf (arxiv.org)

1. 初步了解注意力机制

注意力机制（Attention Mechanism）是近年来在深度学习领域取得显著成果的重要技术之一。

其核心思想是在模型的处理过程中，对输入的不同部分分配不同的权重，从而使模型能够更加关注与当前任务相关的信息。这一机制的引入在自然语言处理、计算机视觉等领域都取得了显著的性能提升，为模型的发展提供了强大的支持。

2. 注意力机制发展的背景

传统的循环神经网络模型在处理序列数据时往往面临着信息丢失和模糊的问题。随着输入序列的增加，模型越来越难有效地捕捉到关键信息，导致性能下降。

为了解决这一问题，注意力机制应运而生。注意力机制可以通过对输入序列中的不同部分分配不同的注意力权重，从而有效地解决这个问题。

最早的注意力机制出现在自然语言处理的机器翻译任务中，通过对齐源语言和目标语言的词语，模型能够更灵活地学习语言间的对应关系，从而提高翻译质量。

3. 注意力机制的架构

注意力机制的基本架构包括查询（Query）、键（Key）和值（Value）的组合。也就是常说的Q、K、V。

在处理输入序列时，模型通过计算查询与键之间的关联度，然后利用这些关联度为每个值分配权重。这些权重决定了模型在计算输出时对输入的关注程度，使得模型能够更有针对性地选择信息。

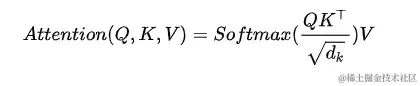
最核心的就是这个公式，但是这个公式确实不太容易理解。下面结合图像来走一遍注意力机制的计算流程。

其实这个公式，就是三个变量，Q、K、V。所以接下来我们会从Q、K、V的角度逐步理解这个公式。

1. 求出Q、K、V

看论文的时候，我很难理解这一点。

Q、K、V到底都是个啥？他们怎么出来的？怎么定义的他们的含义是啥子？作用是啥?

一波激情五连问，把搜索引擎都给干冒烟了。

最后功夫不负有心人，终于在实现代码中看到了Q、K、V的实现，才逐渐理解了。

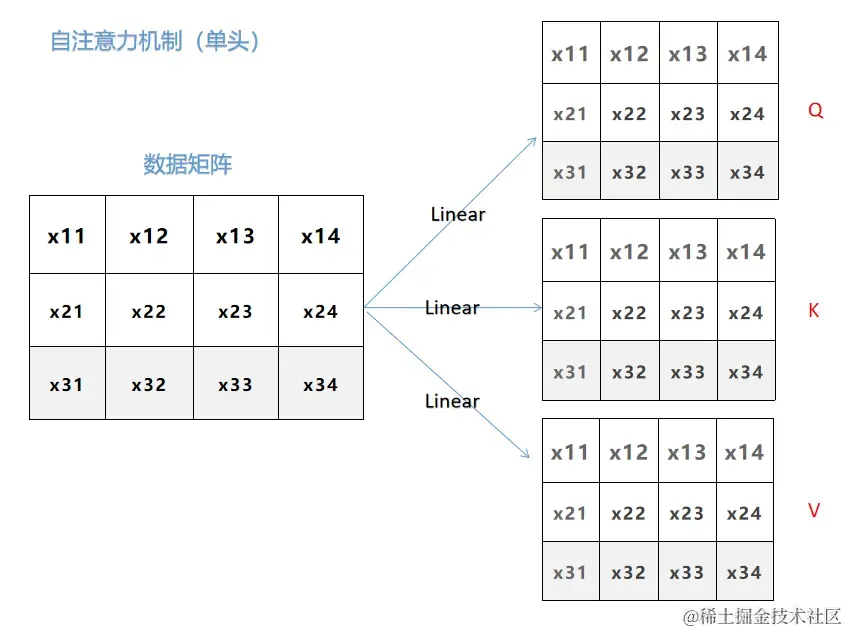
模型中我们会输入数据X，不论是原始数据，时序数据，还是CV的像素矩阵，还是NLP的语义向量，他们都会变成一个数据矩阵的形式。如上图，左半边。

Q、K、V就是通过X过一遍线性层liner计算出来的。

过程非常简单，但是这个含义不简单。

Q、K、V经过的liner层的权重是可学习的，随着训练不断优化调整的，所以Q、K、V也会逐渐趋向我们需要的样子。

2. Q、K、V的用途

为什么要给这个三个变量起这样的名字，查询（Query）、键（Key）和值（Value）。

论文中大致含义是这样的，通过将Q,k相乘，得到注意力得分。

相乘就是非常简单的相乘，然后按列求和，如下代码。

正常来说,是三维矩阵，也不会是torch.mm而是torch.bmm，而且一般矩阵维度相同。但是为了方便理解，就这样来做了。

python
复制代码
q=torch.Tensor([[[3,4],[1,2]],[[3,4],[1,2]],[[3,4],[1,2]]]) # 3*2*2
k=torch.Tensor([[[1,2],[3,4]],[[1,2],[3,4]],[[3,4],[1,2]]]) # 3*2*2
torch.bmm(a,b) # 3*2*2
1
2
3
4
5

这个函数所做的一个事情就是后面剩下的两维对应相乘，由于第一维是3所以要做三次矩阵相乘运算得到3个矩阵，然后再拼接起来，又是322。

这一步操作把我整的很迷惑，为什么相乘，目的是什么，结果为什么能作为权重？

在这里我的理解是，如果没有Q和K，X只是一个简单的iner线性层得到V，这样的权重设置的信息含量太低了，完全就是随机生成，不断拟合而已。

而Q和K都是能够通过学习不断调整的，而且Q和K他们内部都包含了X本身的信息，通过一个比较复杂的运算得到权重，其信息含量会更高。而且Q和K也是通过参考自己不断训练调整得到的，能够学习到的信息更多。权重设置会更合理。

我已经提前声明了，我是个麻瓜，毕竟我连矩阵运算都不太会了。所以这样的理解，简单粗暴，不需要深究公式含义就比较容易理解了。

注意：这里是二维矩阵使用mm方法，三维矩阵才会使用bmm方法。

3. W*V 最终加权和

为了梯度的稳定，注意力机制后续使用了score归一化。

而且也对对score使用softmax激活函数，使其拟合能力更强。

1. W点乘Value值 ，得到加权的每个输入向量的评分
2. 然后相加之后得到最终的输出结果

这里的理解就比较容易了，加权和嘛。

4. 注意力机制的核心实现

python
复制代码
# Self-Attention 机制的实现
class Attention(nn.Module):
    # input x : batch_size * seq_len * input_dim
    # q : batch_size * input_dim * dim_k
    # k : batch_size * input_dim * dim_k
    # v : batch_size * input_dim * dim_v
    def __init__(self, input_dim, dim_k, dim_v):
        super(Discriminator, self).__init__()
        self.q = nn.Linear(input_dim, dim_k)
        self.k = nn.Linear(input_dim, dim_k)
        self.v = nn.Linear(input_dim, dim_v)
        self._norm_fact = 1 / sqrt(dim_k)
        
    def forward(self, x, h):

        Q = self.q(x)  # Q: batch_size * seq_len * dim_k
        K = self.k(x)  # K: batch_size * seq_len * dim_k
        V = self.v(x)  # V: batch_size * seq_len * dim_v

        attention = nn.Softmax(dim=-1)(torch.bmm(Q, K.permute(0, 2, 1))) * self._norm_fact  # Q * K.T() # batch_size * seq_len * seq_len

        output_temp = torch.bmm(attention, V)  # Q * K.T() * V # batch_size * seq_len * dim_v
        output=nn.Sigmoid()(output_temp)
        # print("output",output.shape)

        return output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

在深度学习中，注意力机制的应用有多种形式，例如自注意力机制（Self-Attention）和多头注意力机制（Multi-Head Attention）。

以上的实现就是自注意力机制，多头注意力机制就是组合多个自注意力头来更全面地捕捉输入序列的信息。

最后

为了帮助大家更好的学习人工智能，这里给大家准备了一份人工智能入门/进阶学习资料，里面的内容都是适合学习的笔记和资料，不懂编程也能听懂、看懂，所有资料朋友们如果有需要全套人工智能入门+进阶学习资源包，可以在评论区或扫.码领取哦）~

在线教程

• 麻省理工学院人工智能视频教程 – 麻省理工人工智能课程
• 人工智能入门 – 人工智能基础学习。Peter Norvig举办的课程
• EdX 人工智能 – 此课程讲授人工智能计算机系统设计的基本概念和技术。
• 人工智能中的计划 – 计划是人工智能系统的基础部分之一。在这个课程中，你将会学习到让机器人执行一系列动作所需要的基本算法。
• 机器人人工智能 – 这个课程将会教授你实现人工智能的基本方法，包括：概率推算，计划和搜索，本地化，跟踪和控制，全部都是围绕有关机器人设计。
• 机器学习 – 有指导和无指导情况下的基本机器学习算法
• 机器学习中的神经网络 – 智能神经网络上的算法和实践经验
• 斯坦福统计学习

😝有需要的小伙伴，可以点击下方链接免费领取或者V扫描下方二维码免费领取🆓
​

人工智能书籍

• OpenCV（中文版）.(布拉德斯基等)
• OpenCV+3计算机视觉++Python语言实现+第二版
• OpenCV3编程入门 毛星云编著
• 数字图像处理_第三版
• 人工智能:一种现代的方法
• 深度学习面试宝典
• 深度学习之PyTorch物体检测实战
• 吴恩达DeepLearning.ai中文版笔记
• 计算机视觉中的多视图几何
• PyTorch-官方推荐教程-英文版
• 《神经网络与深度学习》(邱锡鹏-20191121)
• …
  
  😝有需要的小伙伴，可以点击下方链接免费领取或者V扫描下方二维码免费领取🆓
  ​

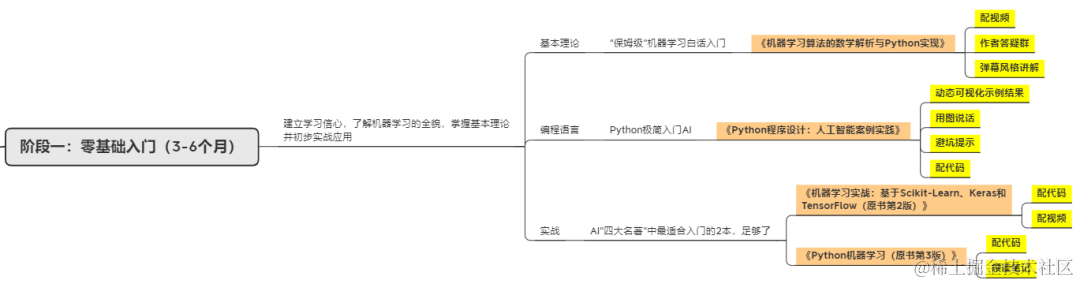
第一阶段：零基础入门（3-6个月）

新手应首先通过少而精的学习，看到全景图，建立大局观。 通过完成小实验，建立信心，才能避免“从入门到放弃”的尴尬。因此，第一阶段只推荐4本最必要的书（而且这些书到了第二、三阶段也能继续用），入门以后，在后续学习中再“哪里不会补哪里”即可。

第二阶段：基础进阶（3-6个月）

熟读《机器学习算法的数学解析与Python实现》并动手实践后，你已经对机器学习有了基本的了解，不再是小白了。这时可以开始触类旁通，学习热门技术，加强实践水平。在深入学习的同时，也可以探索自己感兴趣的方向，为求职面试打好基础。

第三阶段：工作应用

这一阶段你已经不再需要引导，只需要一些推荐书目。如果你从入门时就确认了未来的工作方向，可以在第二阶段就提前阅读相关入门书籍（对应“商业落地五大方向”中的前两本），然后再“哪里不会补哪里”。

😝有需要的小伙伴，可以点击下方链接免费领取或者V扫描下方二维码免费领取🆓
​