-
吴恩达deeplearning.ai:Tensorflow训练一个神经网络
以下内容有任何不理解可以翻看我之前的博客哦:吴恩达deeplearning.ai
在之前的博客中。我们陆续学习了各个方面的有关深度学习的内容,今天可以从头开始训练一个神经网络了。Tensorflow训练神经网络模型
我们使用之前用过的例子:
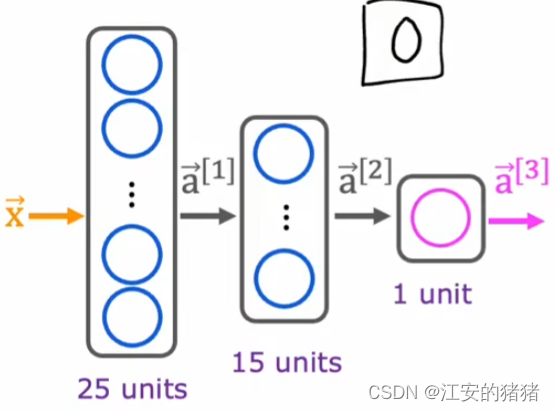
这个神经网络有三层,第一层拥有25个神经元,第二层15个神经元,第三层为最终输出层。
现在提供一个训练集X,一个标签Y,该如何通过代码的形式来表现呢?#1导入工具包 import tensrflow as tf from tensorflow.keras import Sequential from tensorflow.keras.layers import Dense #2创建三个层并让Tensorflow按照顺序将几个层串联起来 model = Sequential([ Dense(units = 25, activation = 'sigmoid') Dense(units = 15, activation = 'sigmoid') Dense(units = 1, activation = 'sigmoid') ]) #3引入工具包,并且让损失函数使用分类交叉熵的形式 from tensorflow.keras.losses import BinaryCrossentropy model.compile(loss = BinaryCrossentropy()) #调用拟合函数,epoch代表训练次数 model.fit(X, Y, epochs=100)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
模型中的一些细节讲解
框架相关
让我们先复习一下之前的内容,如何实现逻辑回归的:
第一步,如何在给定输入特征X和参数W,b的情况下计算输出(定义模型),我们这里经常使用的是sigmoid函数。
第二步,指定损失函数与成本函数
第三步,训练模型,最小化J(w,b)
让我们在训练神经网络的背景下来看看这几步:#1导入工具包 import tensrflow as tf from tensorflow.keras import Sequential from tensorflow.keras.layers import Dense #2创建三个层并让Tensorflow按照顺序将几个层串联起来 model = Sequential([ Dense(units = 25, activation = 'sigmoid') Dense(units = 15, activation = 'sigmoid') Dense(units = 1, activation = 'sigmoid') ])- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
这几段代码说明了神经网络的整个架构体系,告诉你第一层有25个神经元,第二层有15个神经元,第三层一个,采用的激活函数均为sigmoid。
损失函数相关
再写一遍 损失函数的一般数学表达式:
J ( W , B ) = 1 m ∑ L ( f ( x ( i ) , y ( i ) ) J(W,B) = \frac{1}{m}\sum L(f(x^{(i)},y^{(i)}) J(W,B)=m1∑L(f(x(i),y(i))#3引入工具包,并且让损失函数使用分类交叉熵的形式 from tensorflow.keras.losses import BinaryCrossentropy model.compile(loss = BinaryCrossentropy())- 1
- 2
- 3
- 4
这个名叫keras的工具包其实是和tensorflow是完全不同的两个项目开发的,只是最后合入了tensorflow,所有它的工具包需要你单独import。另外,由于工具包的种类真的很多,所以不知道工具包的名字和使用方法时可以上网查找哦。
我们在之前的博客中,曾经学习过二元交叉熵(这是统计学上的叫法),二元的意思是说明这是个布尔值,要么为1要么为0.只是在之前的博客中不叫这个名字,而是为了能够在一个式子之中写出价代价函数:
L ( f ( x ) , y ) = − y l o g ( f ( x ) ) − ( 1 − y ) l o g ( ( 1 − f ( x ) ) L(f(x),y) = -ylog(f(x)) - (1-y)log((1-f(x)) L(f(x),y)=−ylog(f(x))−(1−y)log((1−f(x))
在制定了损失函数之后,Tensorflow就知道了你是希望最小化m个训练的平均值。
如果你是想解决其它类型的问题例如回归问题,你可以给tensorflow指定其它种类的损失函数:from tensorflow.keras.losses import MeanSquareError model.compile(loss = MeanSquareError())- 1
- 2
这是最小化平方误差损失的损失函数。
梯度下降
梯度下降时,你需要重复公式:
w = w − α ∂ ∂ w j J ( w , b ) b = b − α ∂ ∂ b j J ( w , b ) w = w - \alpha\frac{\partial}{\partial w_j}J(w,b)\\ b = b - \alpha\frac{\partial}{\partial b_j}J(w,b) w=w−α∂wj∂J(w,b)b=b−α∂bj∂J(w,b)#调用拟合函数,epoch代表训练次数 model.fit(X, Y, epochs=100)- 1
- 2
Tensorflow使用的是一种叫做反向传播的算法来计算这些偏导数项,只是在函数model.fit中完成的,并告诉它这样迭代100次。
很明显我们现在的代码严重依赖于Tensorflow库,随着技术的发展,大部分工程师都会使用库而非自己重头编起。现在你已经了解了如何自己训练一个神经网络了,在接下来的博客中我们讲讲到一些你可以改变的地方,使得你的神经网络更加强大。
为了给读者你造成不必要的麻烦,博主的所有视频都没开仅粉丝可见,如果想要阅读我的其他博客,可以点个小小的关注哦。 -
相关阅读:
测评瑞萨RZ/G2L存储读写速度与网络
每日一练 | 网络工程师软考真题Day39
【打卡】牛客网:BM36 判断是不是平衡二叉树
Asp .Net Core 系列:Asp .Net Core 集成 Panda.DynamicWebApi
关于版本问题
C++——cv::Rect数据结构详解
Linux | 第一篇——常见指令汇总【超全、超详细讲解】
git的master、develop、feature分支分别是做什么用的?有什么区别和联系?
scss声明全局变量
localStorage实现历史记录搜索功能
- 原文地址:https://blog.csdn.net/m0_75077001/article/details/136281604
