• 【FPGA】线性反馈移位寄存器（LFSR）的Verilog实现

    什么是移位寄存器

    移位寄存器：是指多个寄存器并排相连，前一个寄存器的输出作为下一个寄存器的输入，寄存器中存放的数据在每个时钟周期向左或向右移动一位。

    下面的右移移位寄存器因为左侧没有有效输入，所以在第4个时钟周期，寄存器内就已经没有有效数据了。
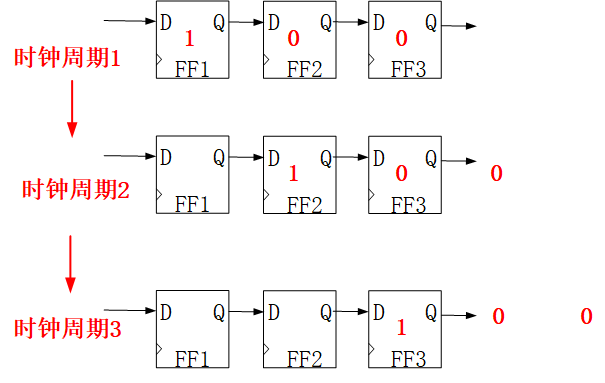
    在这里插入图片描述

    反馈移位寄存器：寄存器被移出的数据后又通过某种方式或函数重新连接到了移位寄存器的输入端，从而使得移位寄存器有不断的输出。
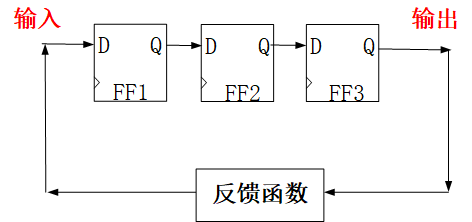
    在这里插入图片描述

    线性反馈移位寄存器（Linear-Feedback Shift Register，LFSR）：当反馈移位寄存器的反馈函数为线性函数时，就称这个移位寄存器是反馈移位寄存器。LFSR所用的线性反馈函数一般为 异或 或者 同或。
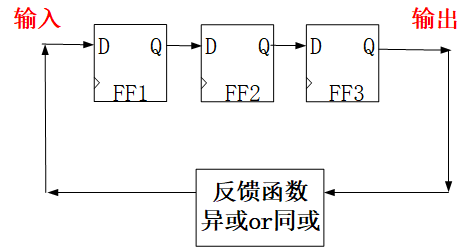
    在这里插入图片描述

    在每个时钟周期，LFSR的新的输入值会被反馈到内部各个寄存器的输入端，输入值中的一部分来源于LFSR的输出端，另一部分来源于LFSR各输出端进行异或运算得到。

    什么是LFSR

    LFSR的初始值被称为种子（Seed）。由异或门构成的LFSR的种子不能为全0，因为0与0异或永远为0，所以移位寄存器的输出永远都不会变化。同理，由同或门构成的LFSR的种子则不能为全1。

    LFSR中的寄存器的个数被称为LFSR的级数。一个3级的LFSR最多同时存放3bit数据。一个n级的LFSR最多只有2^n - 1个状态（因为要排除全0状态 或 全1状态），比如3级的LFSR就只有7个状态。

    LFSR的有些位参与反馈，有些位不参与反馈，其中参与的位被称为抽头。因为触发器编号从1开始，因此抽头的取值范围是1~(2^n-1)。

    如果设计得当（与抽头有关），那么LFSR产生的状态可以是周期性的。只要选择合适的反馈函数便可使序列的周期达到最大值(2^n-1)，周期达到最大值的序列称为m序列（ m-sequence ）。比如下面的LFSR（假设种子为111）会依次产生
    111>110>100>001>010>101>011 这7个状态，然后又重新从111开始循环。
    在这里插入图片描述
    不同的级数如何选取正确的抽头？可以参考下面这个表，表内的抽头选取都是可以保证LFSR能运转到最多状态的。
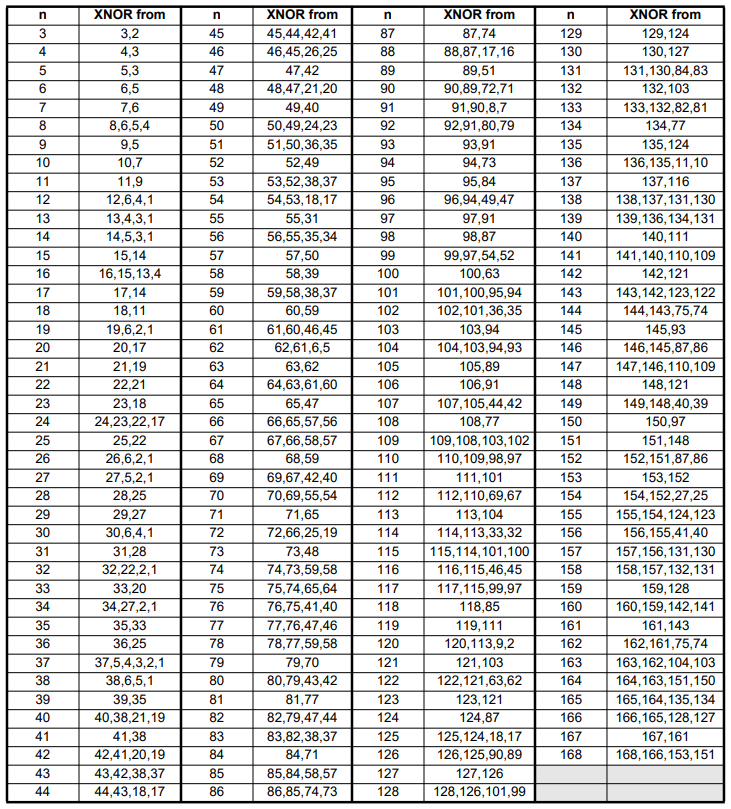
    在这里插入图片描述

    LFSR的两种分类

    目前有两类常用的LFSR：斐波那契LFSR 和 伽罗瓦LFSR，下面分别就进行介绍。

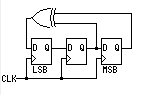
    斐波那契LFSR（Fibonacci LFSRs），又被称为多到一型LFSR，即多个触发器的输出通过反馈来驱动一个触发器的输入。下图是一个典型的斐波那契LFSR，反馈抽头为3和2。
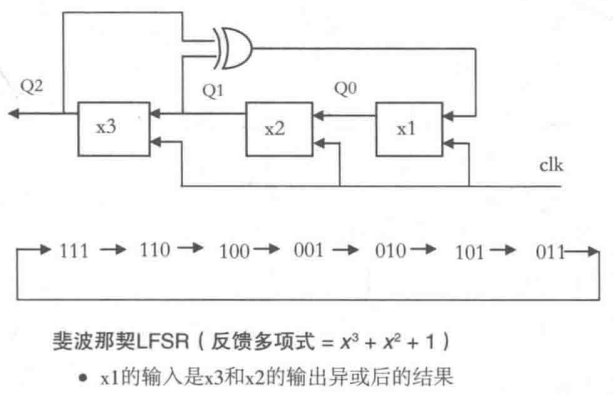
    在这里插入图片描述
    伽罗瓦LFSR（Fibonacci LFSRs），又被称为一到多型LFSR，即以个触发器的输出通过反馈来驱动多个触发器的输入。下图是一个典型的伽罗瓦LFSR，反馈抽头同样为3和2。这个伽罗瓦LFSR同样可以产生7级序列，但是序列的排序与斐波那契LFSR产生的序列是不同的。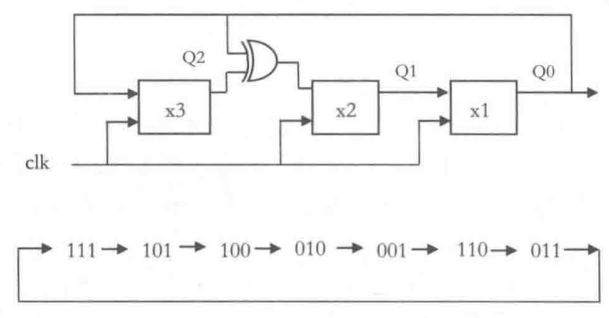

    在这里插入图片描述
    斐波那契LFSR和伽罗瓦LFSR有同样的功能，但是伽罗瓦LFSR的电路性能要由于斐波那契LFSR，因为它在两个触发器之间只使用了一个异或门（或者同或门）。

    Verilog实现与仿真

    下面用Verilog分别实现抽头为（8.6.5.4）的8级斐波那契LFSR和伽罗瓦LFSR，8级LFSR的状态数为2^8-1=255个。
    .
    这个网站LFSR自动工具有一个很好用的LFSR工具，可以自定义抽头、级数，反馈方式和LFSR种类，它可以自动生成Verilog代码和穷举所有的LFSR状态。
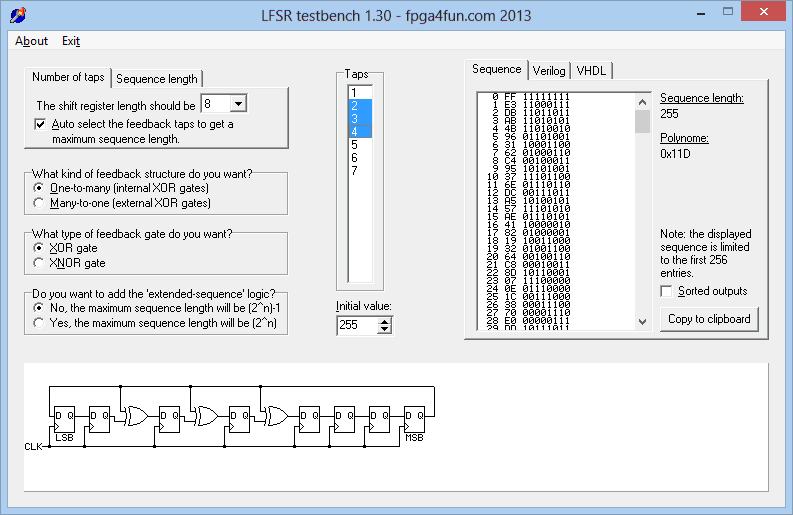
    在这里插入图片描述

    斐波那契LFSR

    用同或门作为反馈函数生成抽头为（8.6.5.4）的8级斐波那契LFSR，Verilog代码如下：

    //8级斐波那契LFSR（多到1型LFSR）设计
//同或门作为反馈函数，反馈多项式为 f(x)=x^8 + x^6 + x^5 + x^4 + 1
module LFSR8_Fib(
	input 				clk,
    input	     	 	rst,	
	output reg [7:0]	lfsr
);

always @(posedge clk) begin
	if(rst)
		//同或门种子可以选取全0，同时FPGA复位后也会复位到0，比较方便
		lfsr <= 8'h0;	
	else begin
		//抽头从1开始为8、6、5、4
		lfsr[0] <= ~(lfsr[3] ^ lfsr[4] ^ lfsr[5] ^ lfsr[7]);
		//低位移动到高位
		lfsr[7:1] <= lfsr[6:0];
	end
end

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19

    生成的LFSR示意图如下：
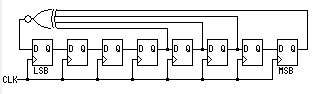
    在这里插入图片描述
    为了验证生成电路的正确性，需要编写TB文件进行验证。对于这种简单的模块（只有255个状态），最简单的验证办法就是穷举所有状态与正确状态进行对比即可。方法有几种：

    方法1：手动对比
    移位LFSR软件提供了所有正确的输出，所以我们只需要将正确的向量与仿真出来的波形结果一一对比即可，这种方法简单，但是效率较低，且容易出错。编写的TB文件如下：

    `timescale 1ns/1ns
module tb_LFSR8_Fib();
//信号声明
reg				clk;
reg				rst;
reg		[7:0] 	cnt;	//记录状态个数，一共255个（没有全1状态）
wire	[7:0]	lfsr;

//模块实例化
LFSR8_Fib	inst_LFSR8_Fib(
	.clk	(clk),
	.rst	(rst),	
	.lfsr   (lfsr)
);	

//生成时钟信号
initial begin
    clk	= 1'b1;
	forever #5 clk = ~clk;
end

//生成复位信号
initial begin
		rst = 1'b1;	//复位
    #45 rst = 1'b0; //取消复位
end

//仿真过程
initial begin
	wait(cnt == 255);	//所有状态都仿真结束
    #10 $stop;			//关闭仿真
end

//记录状态个数，每个有效时钟周期加1
always@(posedge clk)begin
	if(rst)
		cnt <= 8'd0;
	else begin
		cnt <= cnt + 1'd1;
	end
end

endmodule

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43

    仿真结果如下：
    在这里插入图片描述
    与正确向量一一对比即可，发现仿真结果无误。
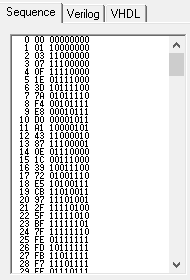
    在这里插入图片描述

    方法2：将仿真结果打印到Tcl窗口，然后复制到文件，再与正确向量对比。对比方式可以是手动对比，也可以是用插件自动进行对比。

    这种方法只需要部分修改TB文件：

    //记录状态个数，每个有效时钟周期加1
always@(posedge clk)begin
	if(rst)
		cnt <= 8'd0;
	else begin
		cnt <= cnt + 1'd1;
		$display("%h",lfsr);	//打印每一个状态到窗口
	end
end

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9

    然后Tcl窗口就打印出了仿真结果：
    在这里插入图片描述
    方法3：基本与方法2类似，只不过将将仿真结果直接打印到文件，再与正确向量对比。对比方式可以是手动对比，也可以是用插件自动进行对比。TB文件如下：

    `timescale 1ns/1ns
module tb_LFSR8_Fib();
//信号声明
reg				clk;
reg				rst;
reg		[7:0] 	cnt;	//记录状态个数，一共255个（没有全1状态）
wire	[7:0]	lfsr;

//定义文件句柄
integer		handle_file_out;	

//模块实例化
LFSR8_Fib	inst_LFSR8_Fib(
	.clk	(clk),
	.rst	(rst),	
	.lfsr   (lfsr)
);	

//生成时钟信号
initial begin
    clk	= 1'b1;
	forever #5 clk = ~clk;
end

//生成复位信号
initial begin
		rst = 1'b1;	//复位
    #45 rst = 1'b0; //取消复位
end

//仿真过程
initial begin
	wait(cnt == 255);	//所有状态都仿真结束
    #10 
	$fclose(handle_file_out);	//关闭文件
	$stop;				//关闭仿真
end

//打开文件file_out，相对路径需要与TB文件在同一目录下
initial begin
	//handle_file_out = $fopen("file_out.txt","w");//相对路径
	handle_file_out = $fopen("G:/file_out.txt","w");//绝对路径
end

//记录状态个数，每个有效时钟周期加1
always@(posedge clk)begin
	if(rst)
		cnt <= 8'd0;
	else begin
		cnt <= cnt + 1'd1;
		//$display("%h",lfsr);	//打印每一个状态到窗口
		//打印每一个状态到文件
		$fdisplay(handle_file_out,"%h",lfsr);	
	end
end

endmodule

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57

    打开file_out文件，可以看到数据都已经被保存好了：
    在这里插入图片描述
    方法4：在TB文件中读取正确向量并自动与仿真结果一一对比，若对比有误则输出某个标志信号。TB文件如下：

    `timescale 1ns/1ns
module tb_LFSR8_Fib();
//信号声明
reg				clk;
reg				rst;
wire	[7:0]	lfsr;

reg		[7:0] 	cnt;				//记录状态个数，一共255个（没有全1状态）
reg		[7:0] 	lfsr_gold [0:254];	//构建一个数组来存储正确向量，位宽为8，个数为255个
reg				flag;				//错误标志，1表示对比错误；0表示对比正确
reg		[7:0]	cnt_error;			//错误计数器

//模块实例化
LFSR8_Fib	inst_LFSR8_Fib(
	.clk	(clk),
	.rst	(rst),	
	.lfsr   (lfsr)
);	

//生成时钟信号
initial begin
    clk	= 1'b1;
	forever #5 clk = ~clk;
end

//生成复位信号
initial begin
		rst = 1'b1;	//复位
    #45 rst = 1'b0; //取消复位
end

//读取正确向量
initial begin
	$readmemh("G:/file_in.txt",lfsr_gold);	//绝对路径
end

//仿真过程
initial begin
	wait(cnt == 255);	//所有状态都仿真结束
	if (cnt_error == 0)
		//打印仿真成功信息
		$display("simulation succeed!");
	else
		//打印仿真错误信号
		$display("simulation failed,there is %d errors!",cnt_error);
	#10 $stop;			//关闭仿真	
end

//记录状态个数，每个有效时钟周期加1
always@(posedge clk)begin
	if(rst)begin
		cnt <= 8'd0;
		flag <= 1'b0;
		cnt_error <= 8'd0;
	end	
	else begin
		cnt <= cnt + 1'd1;
		if(lfsr_gold[cnt] != lfsr)begin	//如果对比有误
			//$display("cnt=%d is wrong",cnt);	//打印错误的地方
			flag <= 1'b1;				//拉高错误标志
			cnt_error <= cnt_error + 1;	//错误计数器加1
		end
		else begin
			flag <= 1'b0;
			cnt_error <= cnt_error;
		end	
	end
end

endmodule

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70

    为了对比仿真结果，我故意把正确向量的第2个数据改成错误数据，仿真结果如下：
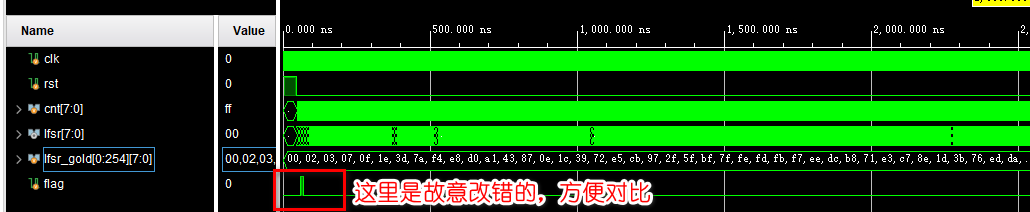
    在这里插入图片描述
    Tcl窗口也打印了错误：
    在这里插入图片描述
    把正确向量的错误修正后再仿真，仿真无误，打印的信息如下：
    在这里插入图片描述
    这种方式可以自动对比正确向量与仿真结果，大大提高了效率。

    伽罗瓦LFSR

    用同或门作为反馈函数生成抽头为（8.6.5.4）的8级伽罗瓦LFSR，Verilog代码如下：

    //8级伽罗瓦LFSR（1到多型LFSR）设计
//同或门作为反馈函数，反馈多项式为 f(x)=x^8 + x^6 + x^5 + x^4 + 1
module LFSR8_Gal(
	input 				clk,
    input	     	 	rst,	
	output reg [7:0]	lfsr
);

wire feedback;;

assign feedback = lfsr[7];

always @(posedge clk)begin
	if(rst)
		//同或门种子可以选取全0，同时FPGA复位后也会复位到0，比较方便
		lfsr <= 8'h0;
	else begin
		//抽头从1开始为8、6、5、4
		lfsr[0] <= feedback;
		lfsr[1] <= lfsr[0];
		lfsr[2] <= lfsr[1];
		lfsr[3] <= lfsr[2];
		lfsr[4] <= lfsr[3] ~^ feedback;
		lfsr[5] <= lfsr[4] ~^ feedback;
		lfsr[6] <= lfsr[5] ~^ feedback;	
		lfsr[7] <= lfsr[6];
	end	
end

endmodule

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30

    电路示意图如下：
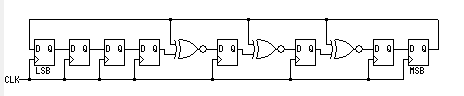
    在这里插入图片描述
    仿真脚本依然用上面的即可，这里就不啰嗦了。

    禁止状态的处理

    用同或门作为反馈函数的LFSR是禁止使用全1状态的，因为全1的同或还是1，会导致移位寄存器一直处于全1状态出不来。这是的n级的LFSR只有2^n - 1 个状态，比一般的计数器状态少1个。如果需要完善这种禁止状态的处理，可以增加一部分电路来改变。

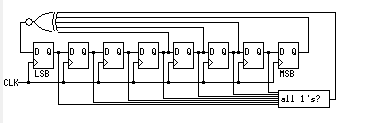
    斐波那契LFSR可以增加一个判断寄存器是否为全1的电路，并将其输出连接到同或门，示意图如下：
    在这里插入图片描述
    如果不为全1状态，则全1判断电路输出为0，0异或任何数都等于该数本身，即不会对原有电路造成影响。如果为全1状态，则全1判断电路输出为1，此时同或门的输出为0，所以下一个状态的最低位即为0，也就是说跳出了全1状态。

    这部分的Verilog代码如下：

    //8级斐波那契LFSR（多到1型LFSR）设计
//同或门作为反馈函数，反馈多项式为 f(x)=x^8 + x^6 + x^5 + x^4 + 1
module LFSR8_Fib(
	input 				clk,
    input	     	 	rst,	
	output reg [7:0]	lfsr
);

always @(posedge clk) begin
	if(rst)
		//同或门种子可以选取全0，同时FPGA复位后也会复位到0，比较方便
		lfsr <= 8'h0;	
	else begin
		//抽头从1开始为8、6、5、4；增加全1状态的跳出
		lfsr[0] <= ~(lfsr[3] ^ lfsr[4] ^ lfsr[5] ^ lfsr[7] ^ (lfsr[6:0]==7'b1111111));
		//低位移动到高位
		lfsr[7:1] <= lfsr[6:0];
	end
end

endmodule

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21

    仿真也没问题，能从全1状态跳出：
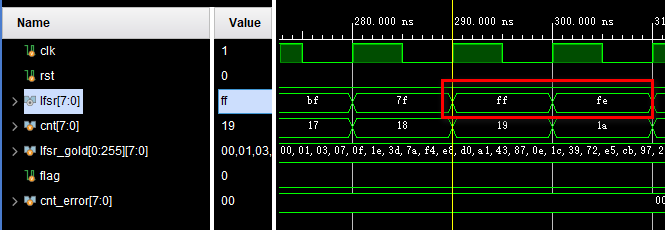
    在这里插入图片描述
    同理，伽罗瓦LFSR也可以增加一个判断寄存器是否为全1的电路，并将其输出连接到同或门，示意图如下：
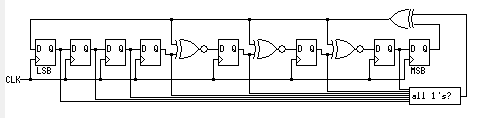
    在这里插入图片描述
    如果不为全1状态，则全1判断电路输出为0，0异或任何数都等于该数本身，即不会对原有电路造成影响。如果为全1状态，则全1判断电路输出为1，此时异或门的输出为0，所以下一个状态的抽头位全变为0，也就是说跳出了全1状态。

    这部分的Verilog代码如下：

    //8级伽罗瓦LFSR（1到多型LFSR）设计
//同或门作为反馈函数，反馈多项式为 f(x)=x^8 + x^6 + x^5 + x^4 + 1
module LFSR8_Gal(
	input 				clk,
    input	     	 	rst,	
	output reg [7:0]	lfsr
);

wire feedback;;

//增加全1状态的跳出
assign feedback = lfsr[7] ^ (lfsr[6:0]==7'b1111111);;

always @(posedge clk)begin
	if(rst)
		//同或门种子可以选取全0，同时FPGA复位后也会复位到0，比较方便
		lfsr <= 8'h0;
	else begin
		//抽头从1开始为8、6、5、4
		lfsr[0] <= feedback;
		lfsr[1] <= lfsr[0];
		lfsr[2] <= lfsr[1];
		lfsr[3] <= lfsr[2];
		lfsr[4] <= lfsr[3] ~^ feedback;
		lfsr[5] <= lfsr[4] ~^ feedback;
		lfsr[6] <= lfsr[5] ~^ feedback;	
		lfsr[7] <= lfsr[6];
	end	
end

endmodule

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31

    仿真也没问题，能从全1状态跳出：
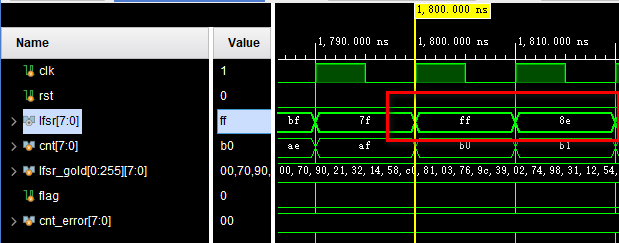
    在这里插入图片描述

    LFSR的用途

    • 构建伪随机数序列，合适的LFSR可以生成一串循环的序列，当寄存器数量足够多时，这些数据可以看做是“伪随机”的，不是真正随机的是因为这些数据都可以根据之前状态而推断得到。
    • 构建计数器。LFSR构建的计数器，虽然每个状态不是+1，但事前计算好其状态跳转时间，依然可以构建特定计数的计数器。这比一般的+1累加计数器更节省资源，且时序性能更好。
    • 加扰和解扰。LFSR可用来对数据进行简单的加扰和解扰。数据发送前和LFSR生成的序列异或，接收端接收到数据后采用同样的LFSR来进行异或操作即可完成解扰。
    • 其他领域，如密码系统，BIST（内建自测试）等等。
    • 📣您有任何问题，都可以在评论区和我交流📃！
    • 📣本文由 孤独的单刀 原创，首发于CSDN平台🐵，博客主页：wuzhikai.blog.csdn.net
    • 📣您的支持是我持续创作的最大动力！如果本文对您有帮助，还请多多点赞👍、评论💬和收藏⭐！
  • 相关阅读:
    实例演示如何使用CCE XGPU虚拟化
    自定义HandlerMethodArgumentResolver如何注册到springmvc框架里的
    idea和eclipse复制一行快捷键
    Shellshock
    如何对ppt文件设置修改权限？
    ssldump一键分析网络流量（KALI工具系列二十二）
    伪分布Hadoop的安装与部署
    读书笔记-《ON JAVA 中文版》-摘要4
    对话永洪科技CEO何春涛：专注BI，决胜AI时代丨数据猿专访
    MATLAB | 官方举办的动图绘制大赛 | 第一周赛情回顾
  • 原文地址：https://blog.csdn.net/wuzhikaidetb/article/details/136287042