-
【Algorithms 4】算法(第4版)学习笔记 09 - 3.2 二叉查找树
文章目录
- 前言
- 参考目录
- 学习笔记
- 1:二叉树与二叉搜索树定义
- 1.1:二叉树定义
- 1.2:二叉搜索树定义
- 1.3:Java定义
- 1.4:BST基本实现
- 1.5:BST demo 演示
- 1.5.1:节点搜索成功命中演示
- 1.5.2:节点搜索未命中演示
- 1.5.3:节点插入演示
- 1.6:BST 查找:Java 实现
- 1.7:BST 插入:Java 实现
- 1.8:树的形状
- 1.9:BSTs 与快速排序分区的一致性
- 1.10:小结
- 2:排序操作
- 2.1:向上取整与向下取整
- 2.1.1:向下取整过程演示
- 2.1.2:向下取整代码实现
- 2.2:小结
- 3:删除操作
- 3.1:删除最大键和删除最小键
- 3.1.1:删除最小项过程演示
- 3.1.2:删除最小项代码实现
- 3.2:删除操作
- 3.2.1:Hibbard 删除
- 3.2.2:Hibbard 删除代码实现
- 3.3:删除操作分析
- 3.4:小结
前言
本文的主要内容是 二叉搜索树 (binary search trees,以下简称 BST)以及其相关的 API 操作介绍。
参考目录
- B站 普林斯顿大学《Algorithms》视频课
(请自行搜索。主要以该视频课顺序来进行笔记整理,课程讲述的教授本人是该书原版作者之一 Robert Sedgewick。) - 微信读书《算法(第4版)》
(本文主要内容来自《3.2 二叉查找树》) - 官方网站
(有书本配套的内容以及代码)
学习笔记
注1:下面引用内容如无注明出处,均是书中摘录。
注2:所有 demo 演示均为视频 PPT demo 截图。1:二叉树与二叉搜索树定义
定义:BST是对称顺序的二叉树。
1.1:二叉树定义
二叉树要么为空, 要么由两个不相交的二叉树组成(即左子树和右子树)。
进一步理解(有点绕):
- 一个二叉树可以是一个空树(null)。
- 否则,它是一个包含一个根节点的树,该节点连接到两个独立的二叉树上,分别称为其左子树和右子树,且左子树和右子树也是二叉树结构。
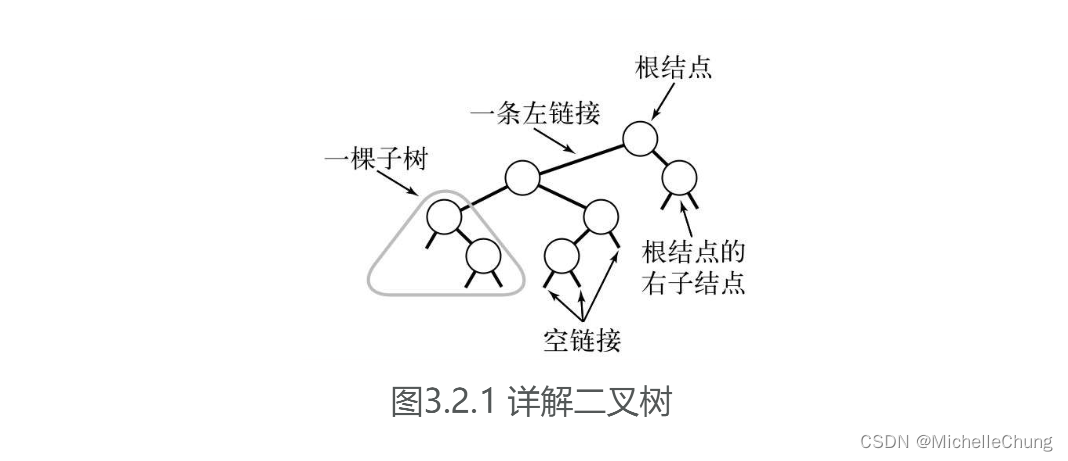
二叉树是一种显式数据结构(显式树结构),与之相对应的,堆是一种隐式数据结构(用数组隐式表示树)。
1.2:二叉搜索树定义
对称顺序。每个节点都有一个键(key),并且每个节点的键都满足以下条件:
- 大于其左子树中所有节点的键。
- 小于其右子树中所有节点的键。
进一步理解:
- 对于二叉树中的任意节点,其键值严格大于其左子树中所有节点的键值。
- 同时,该节点的键值严格小于其右子树中所有节点的键值。
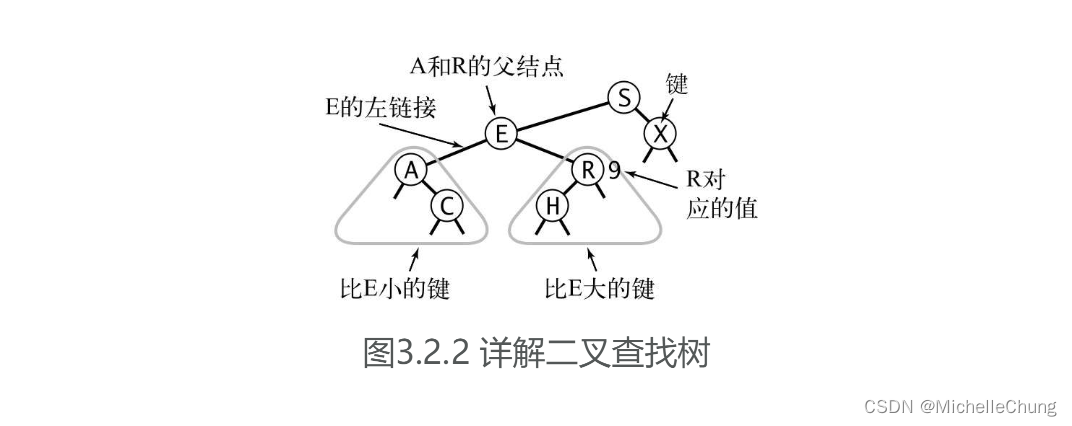
1.3:Java定义
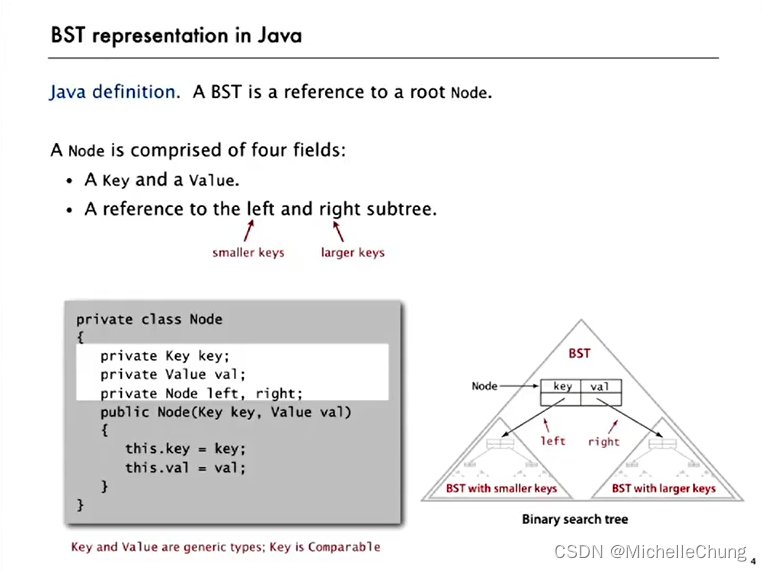
一个二叉搜索树(BST)是一个指向根节点的引用。
一个节点由四个部分组成:
- 一个键(Key)和一个对应的值(Value)。
- 分别指向其左子树(更小的 key)和右子树(更大的 key)的引用。
1.4:BST基本实现
edu.princeton.cs.algs4.BST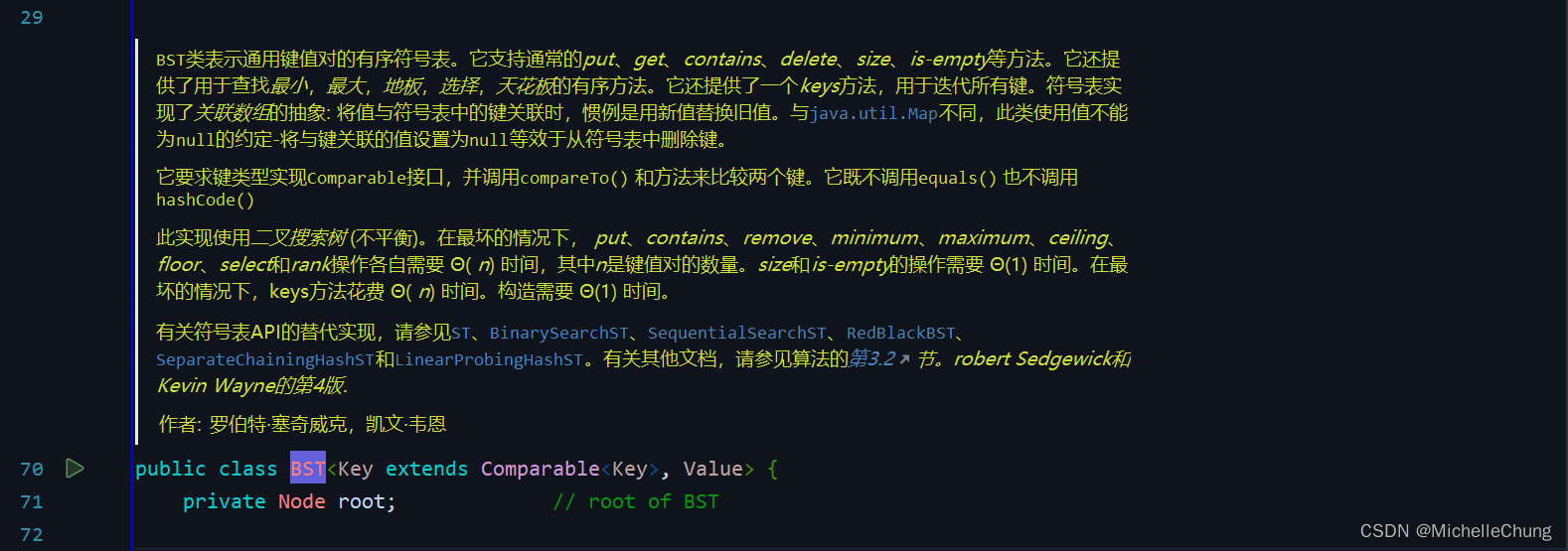
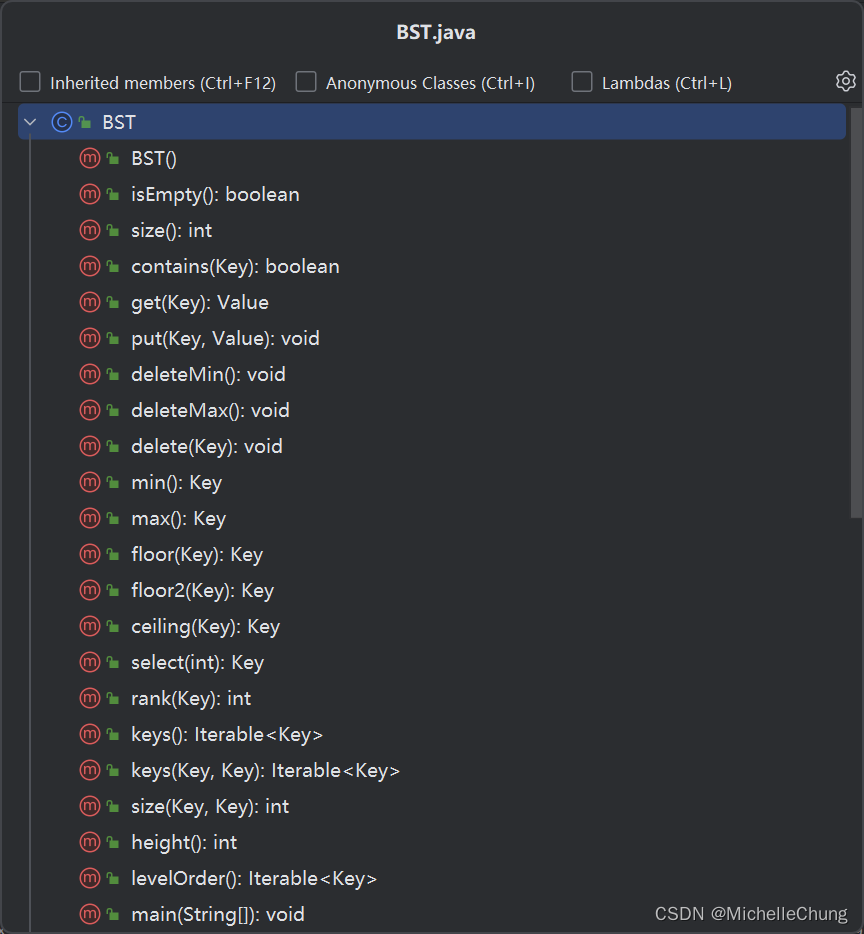
1.5:BST demo 演示
查找:如果更小,向左移动;如果更大,向右移动;如果相等,搜索命中。
1.5.1:节点搜索成功命中演示
搜索 H:
初始状态:
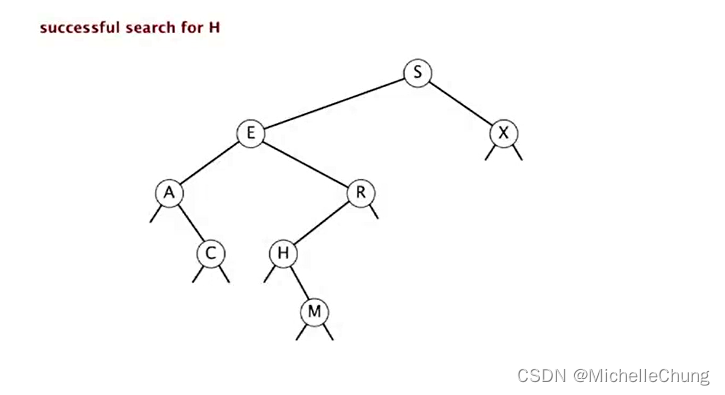
与根节点 S 比较(更小),左移:
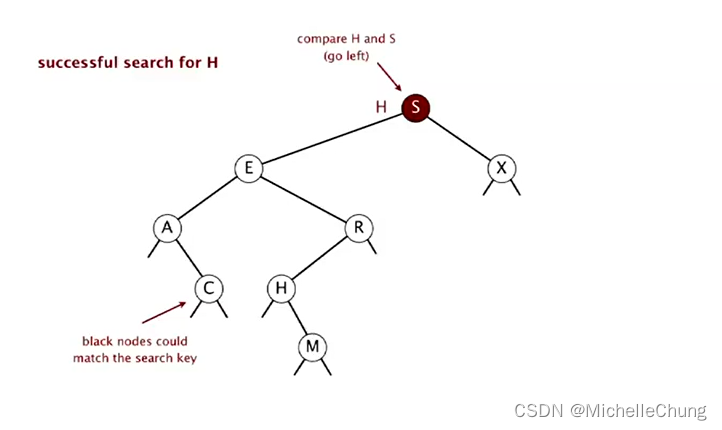
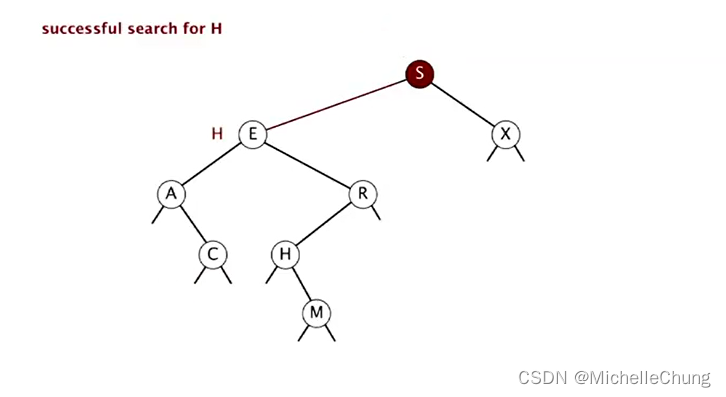
与节点 S 左子树节点 E 比较(更大),右移:
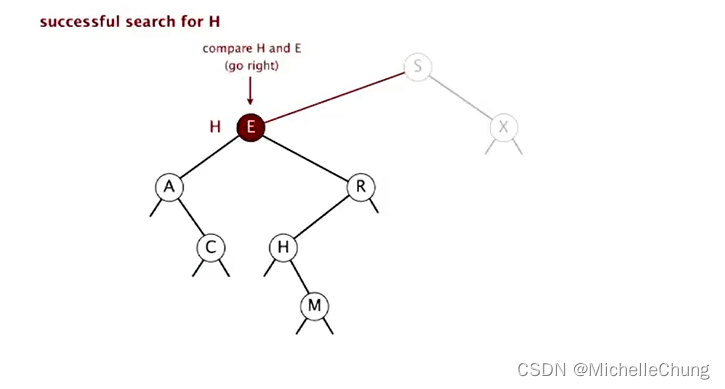
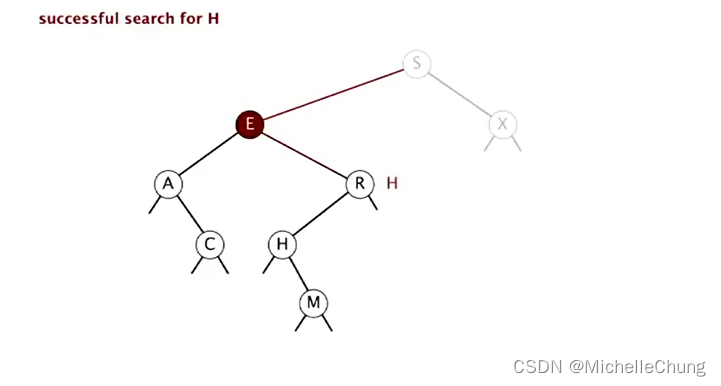
与节点 E 右子树节点 R 比较(更小),左移:
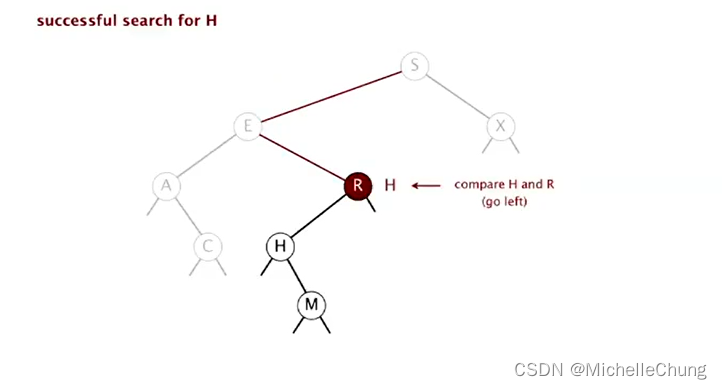
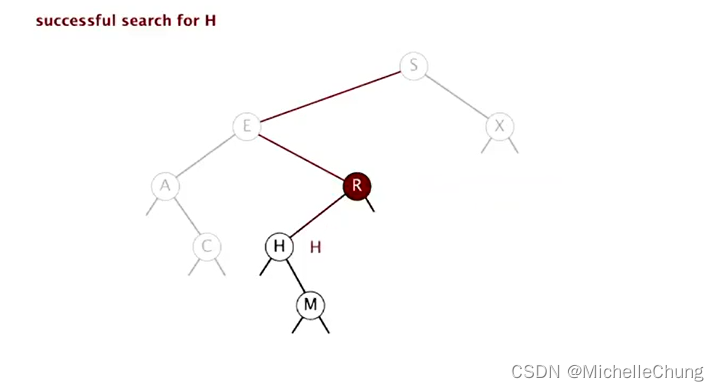
与节点 R 左子树节点 H 比较(相等),搜索命中:
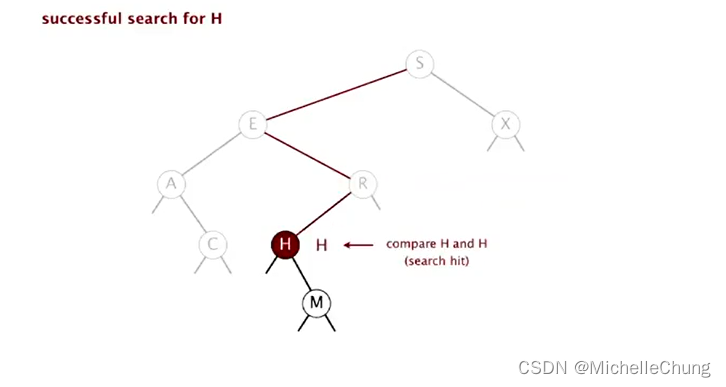
1.5.2:节点搜索未命中演示
搜索 G:
初始状态:
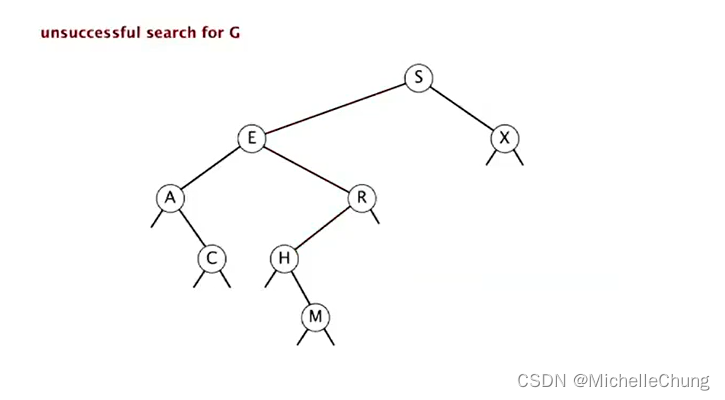
与根节点 S 比较(更小),左移:
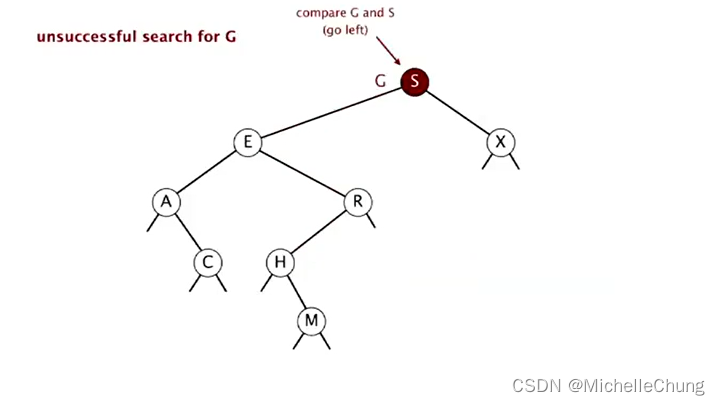
与节点 S 左子树节点 E 比较(更大),右移:
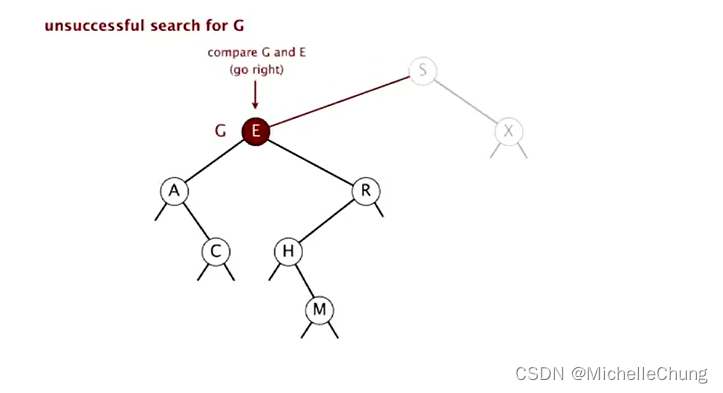
与节点 E 右子树节点 R 比较(更小),左移:
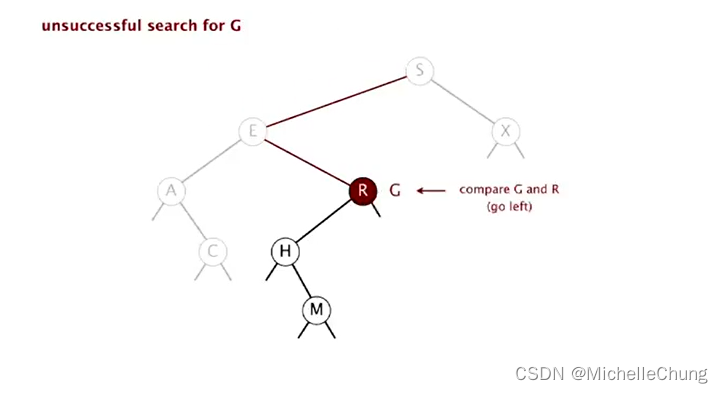
与节点 R 左子树节点 H 比较(更小),左移:
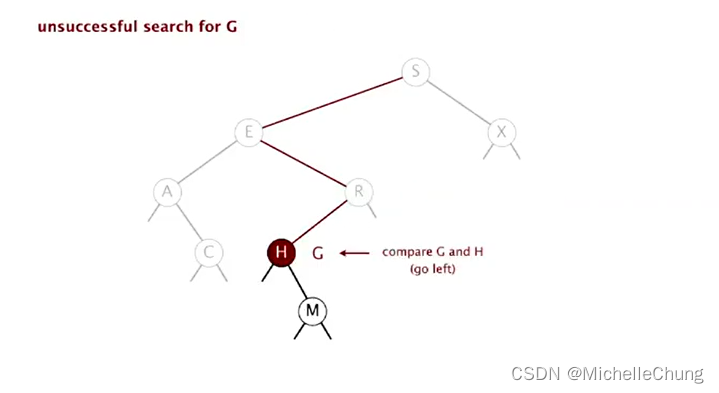
H 左移为空链接,查找未命中(并返回 null):
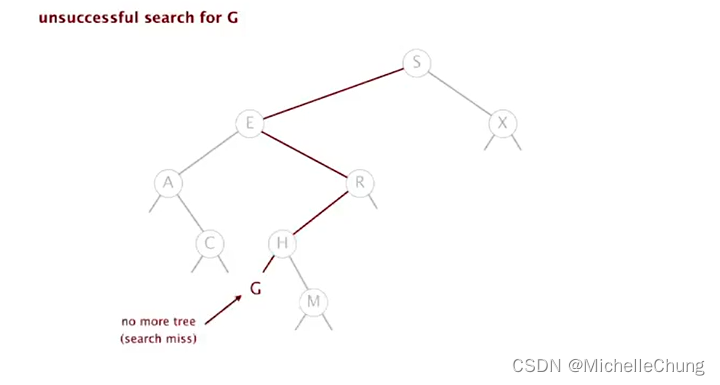
1.5.3:节点插入演示
插入:如果更小,向左移动;如果更大,向右移动;如果为 null,插入。
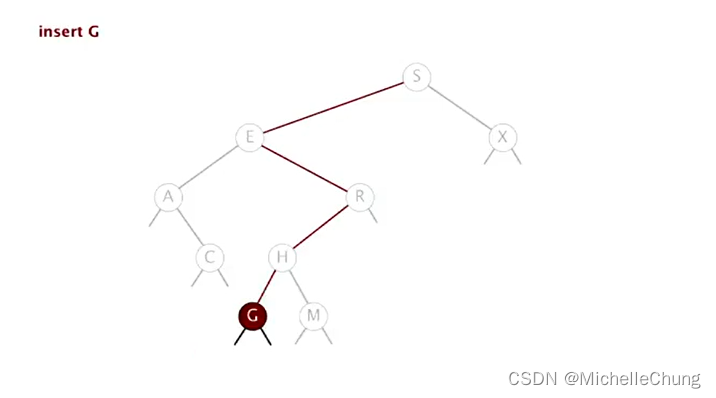
插入 G:
初始状态:
移动路径与
#1.5.2查找类似,直到节点 H 左子树为 null,插入节点 G: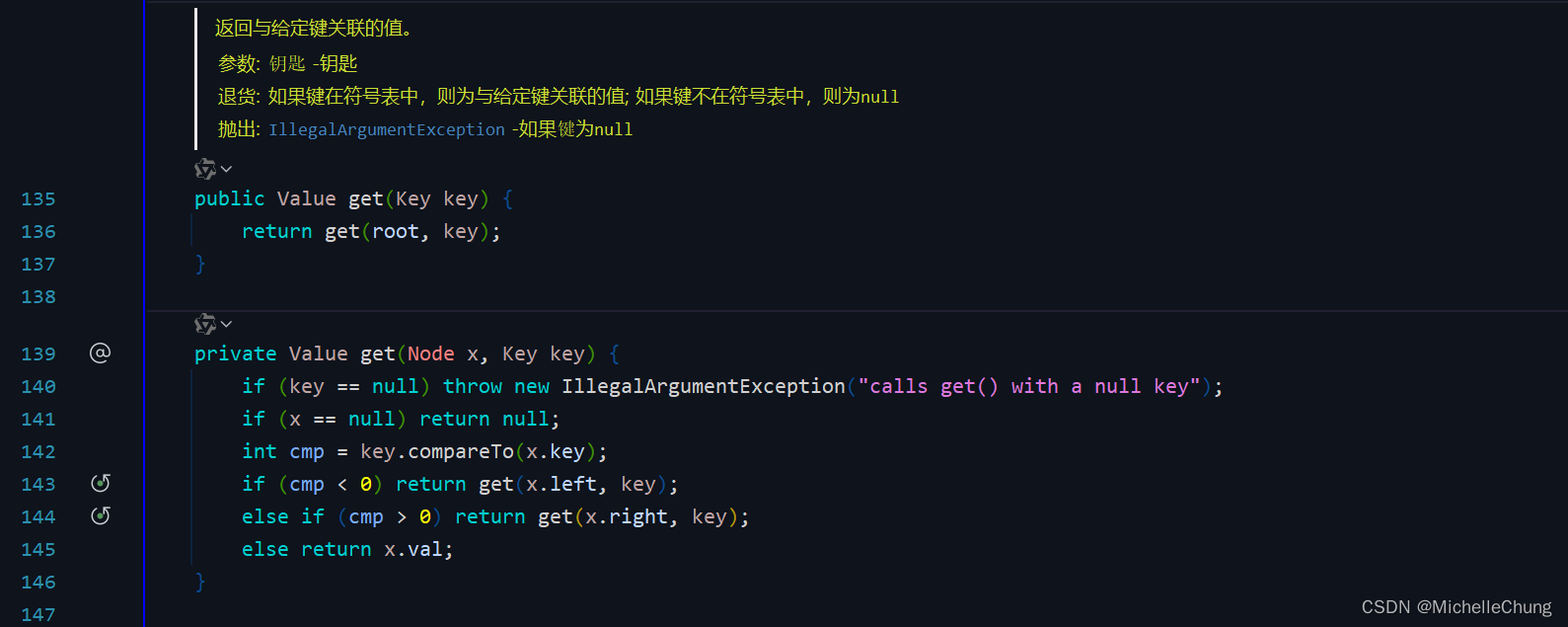
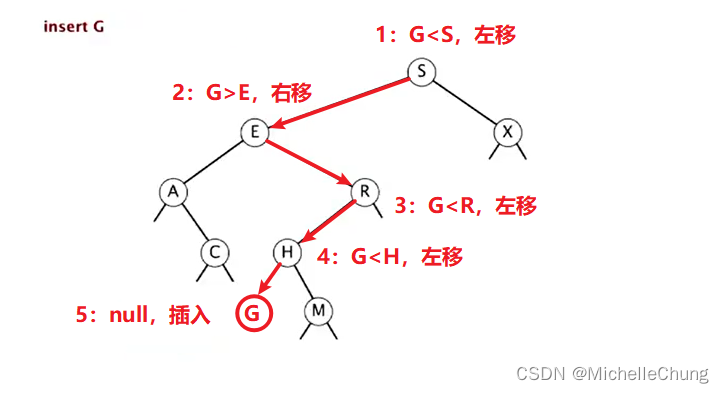
G 完整移动路线图:
1.6:BST 查找:Java 实现
edu.princeton.cs.algs4.BST#get
开销:
一次结束于给定结点的命中查找所需的比较次数为查找路径的深度加1。
1.7:BST 插入:Java 实现
edu.princeton.cs.algs4.BST#put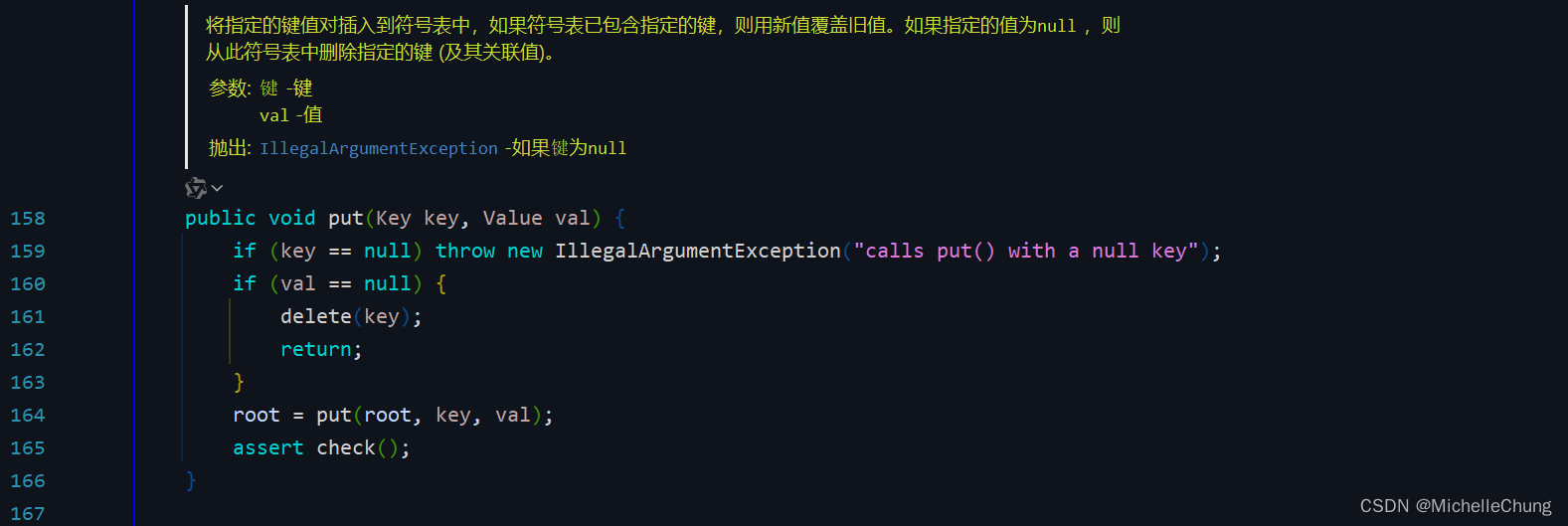
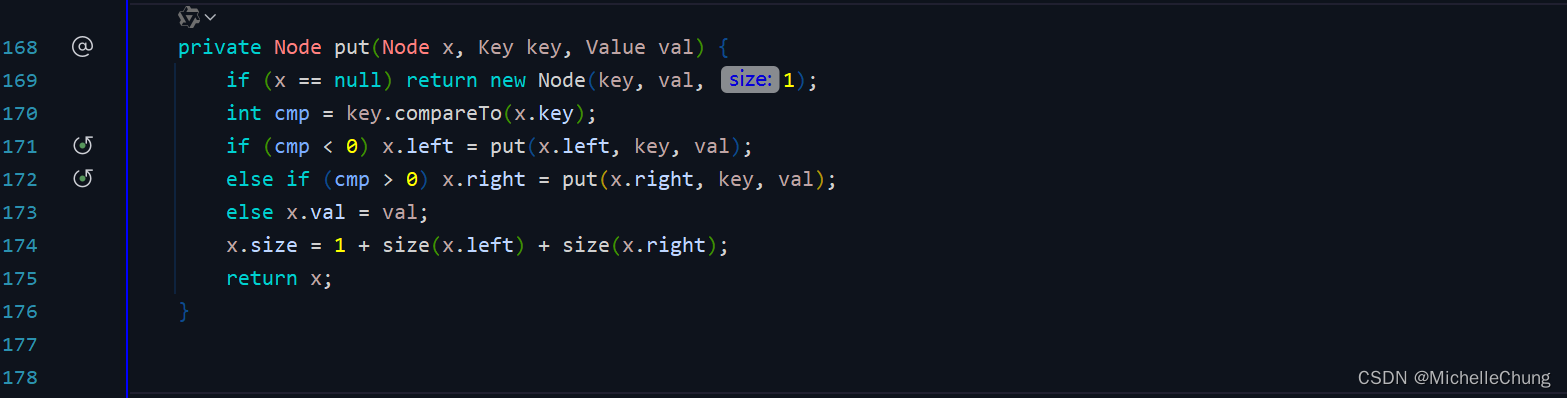
1.8:树的形状
- 许多 BSTs 对应同一组keys
- 一次查找 / 插入所需的比较次数为查找路径的深度加1。
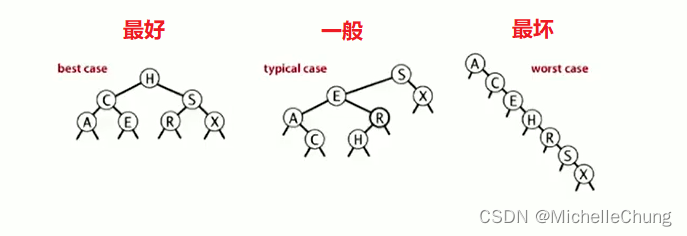
注:树的形状取决于键被插入的先后顺序。
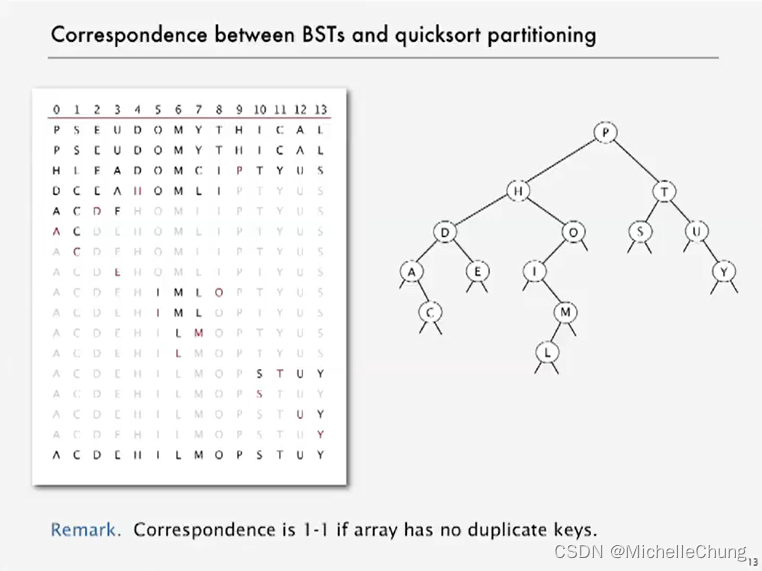
1.9:BSTs 与快速排序分区的一致性

命题C。在由N个随机键构造的二叉查找树中,查找命中平均所需的比较次数为~2lnN(约1.39lgN)。
命题D。在由N个随机键构造的二叉查找树中插入操作和查找未命中平均所需的比较次数为~2lnN(约1.39lgN)。

1.10:小结
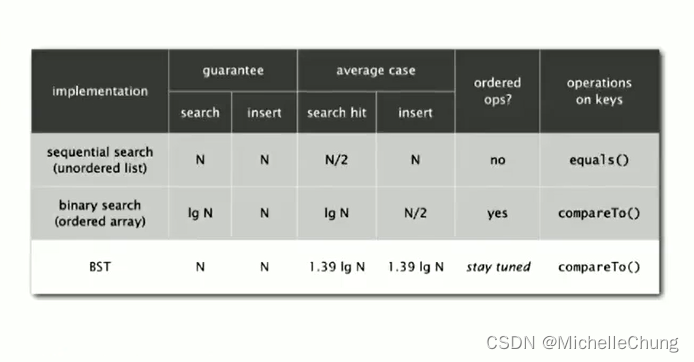
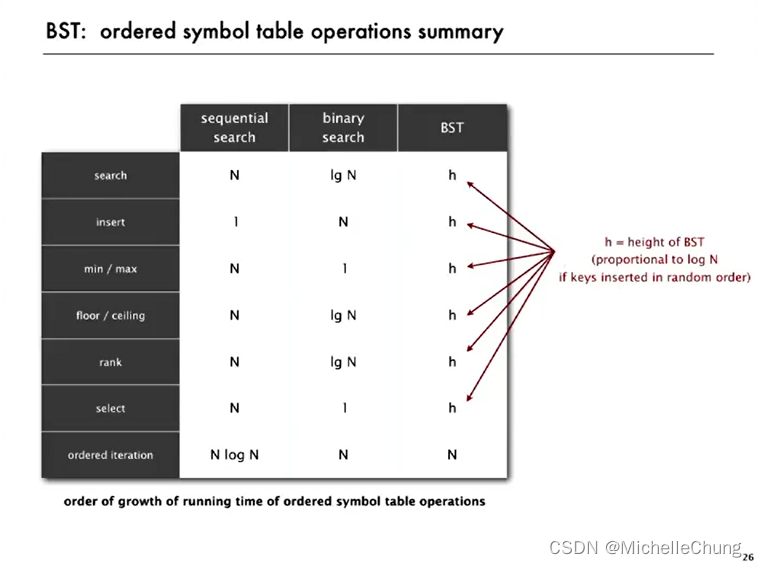
书里面在章节末尾也有给出相关的表格:
表3.2.2 简单的符号表实现的成本总结

2:排序操作
Now,we’re going to take a look at ordered symbol table operations using the binary search tree data structure as the underlying implementation.
现在,我们将要探讨如何利用二叉搜索树这一数据结构作为底层实现,来进行有序符号表操作。相关的所有章节:
- 3.2.3.1 最大键和最小键
Minimum and maximum. - 3.2.3.2 向上取整和向下取整
Floor and ceiling. - 3.2.3.3 选择操作
Selection. - 3.2.3.4 排名
Rank.
2.1:向上取整与向下取整
2.1.1:向下取整过程演示
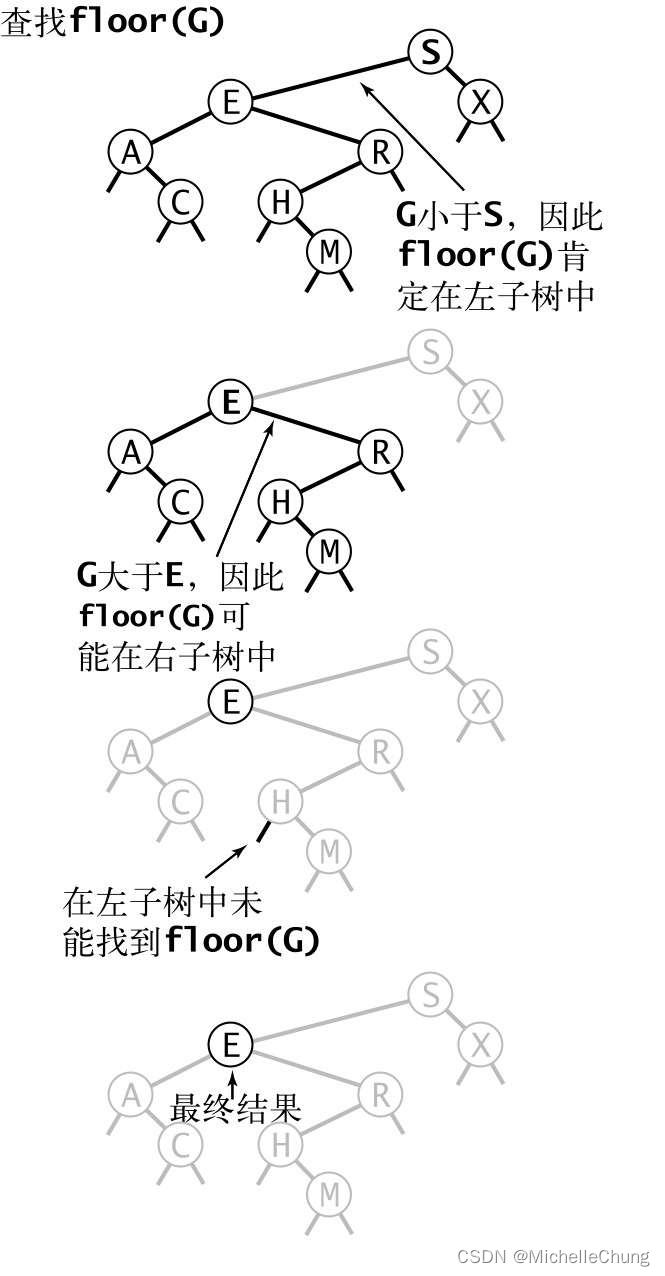
图3.2.10 计算floor()函数2.1.2:向下取整代码实现
edu.princeton.cs.algs4.BST#floor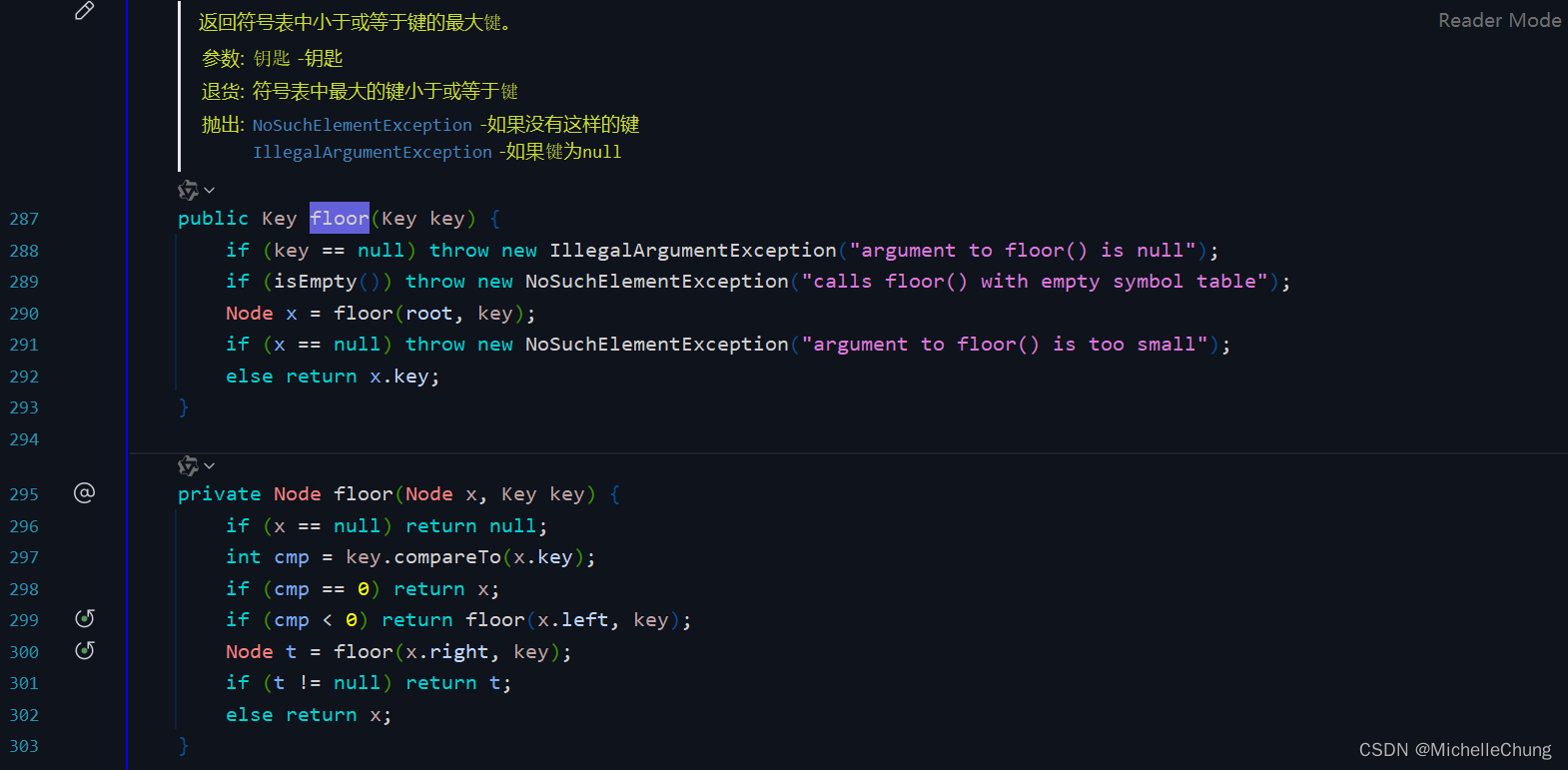
2.2:小结
3:删除操作
相关的所有章节:
- 3.2.3.5 删除最大键和删除最小键
Delete the minimum and maximum. - 3.2.3.6 删除操作
Delete. - 3.2.3.7 范围查找
Range search. - 3.2.3.8 性能分析
3.1:删除最大键和删除最小键
3.1.1:删除最小项过程演示
- 向左移动,直到找到左链接为空的节点。
- 将该节点替换为其右侧链接。
- 更新子树计数。
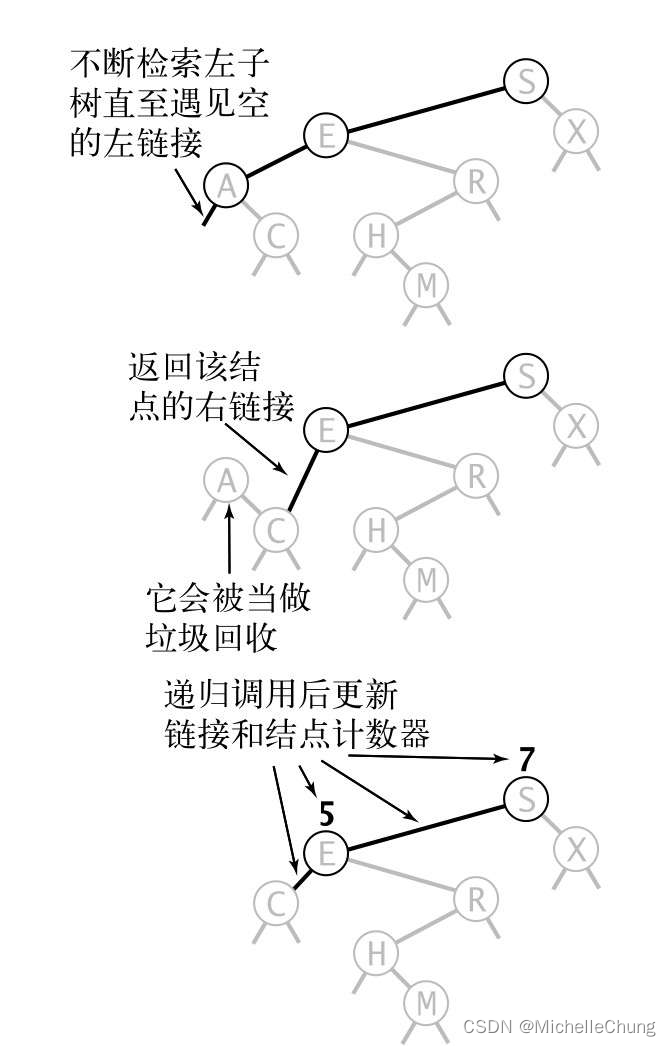
图3.2.12 删除二叉查找树中的最小结点3.1.2:删除最小项代码实现
edu.princeton.cs.algs4.BST#deleteMin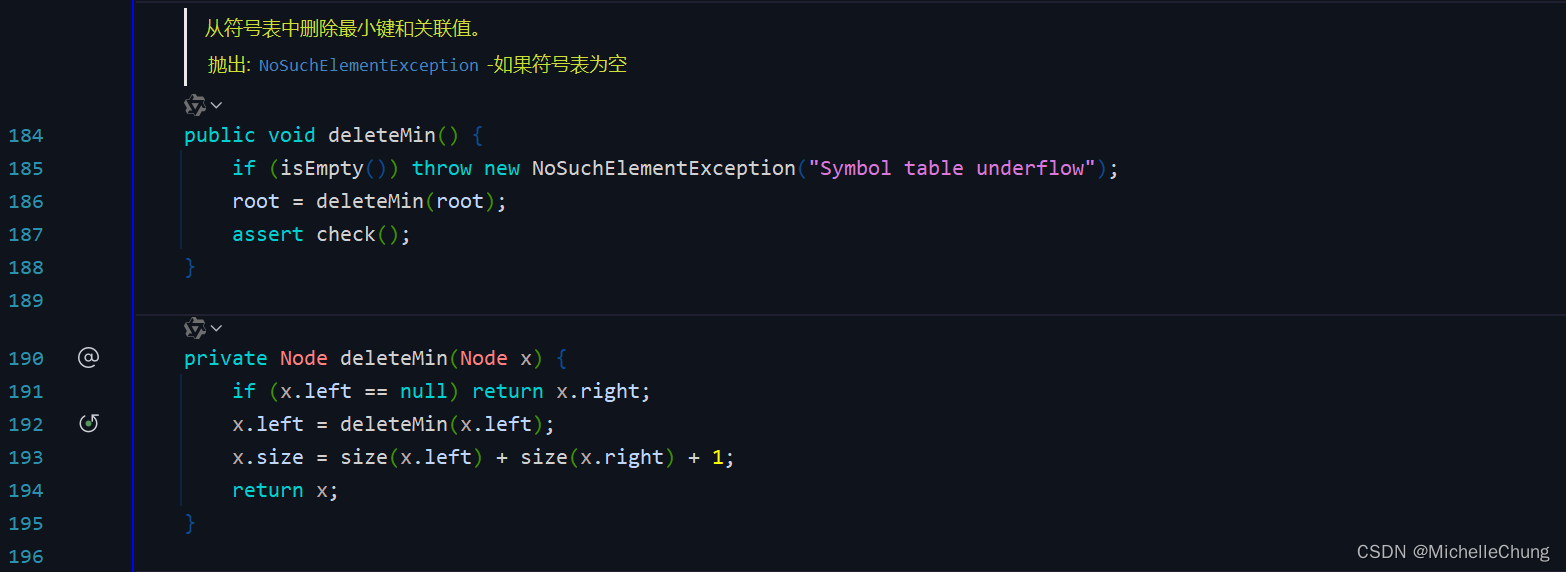
3.2:删除操作
3.2.1:Hibbard 删除
情况一:没有子节点
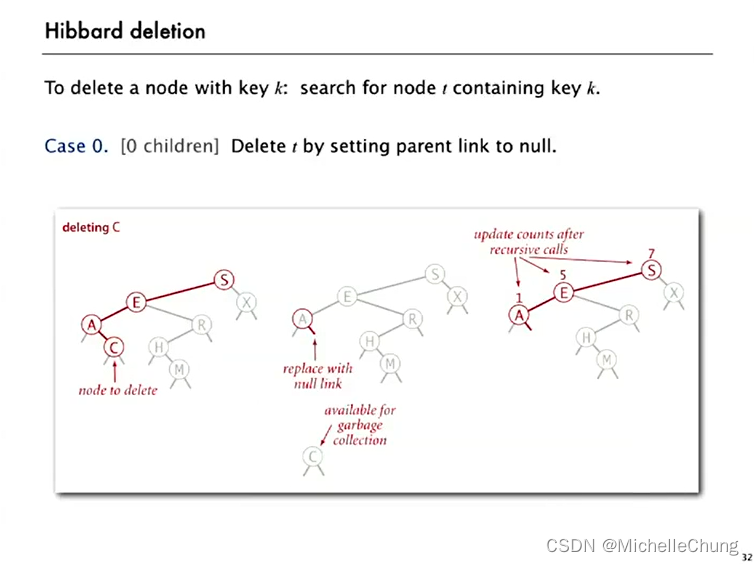
情况二:一个子节点

情况三:两个子节点
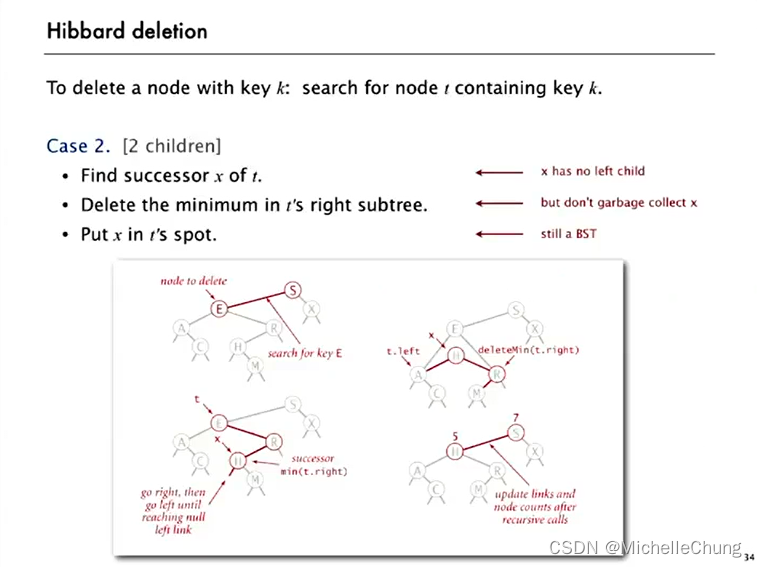
书中关于删除过程操作的描述:
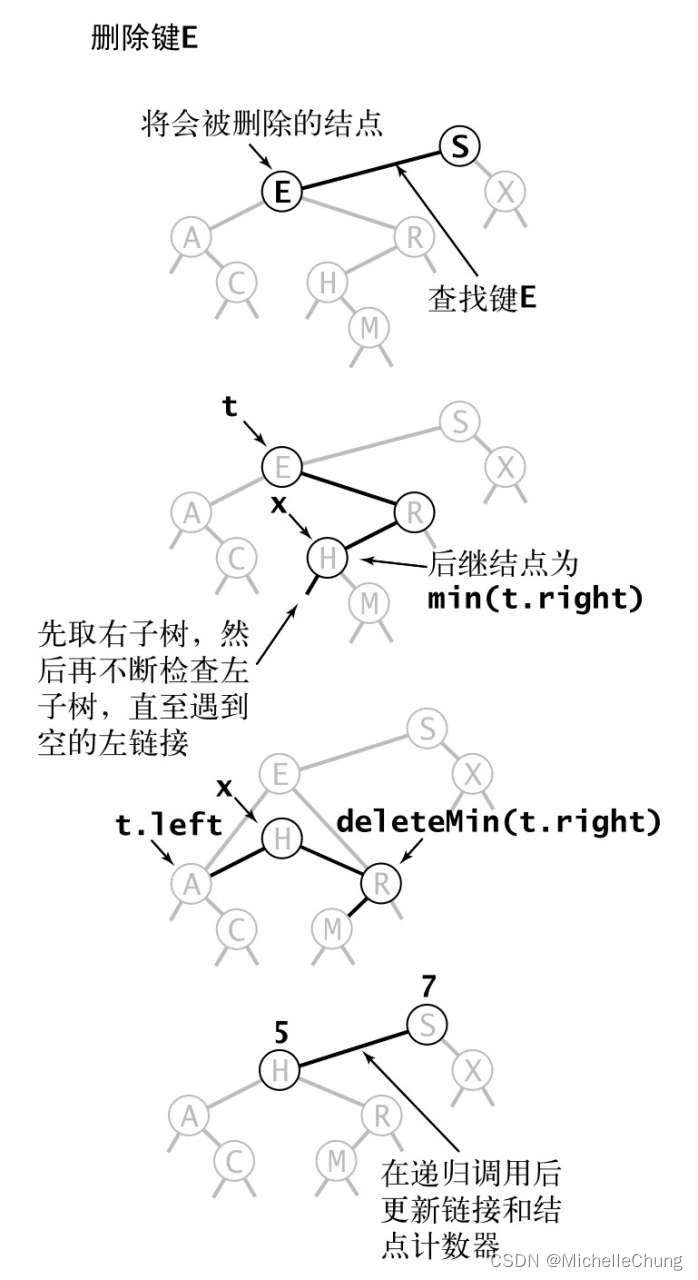
图3.2.13 二叉查找树中的删除操作
3.2.2:Hibbard 删除代码实现
edu.princeton.cs.algs4.BST#delete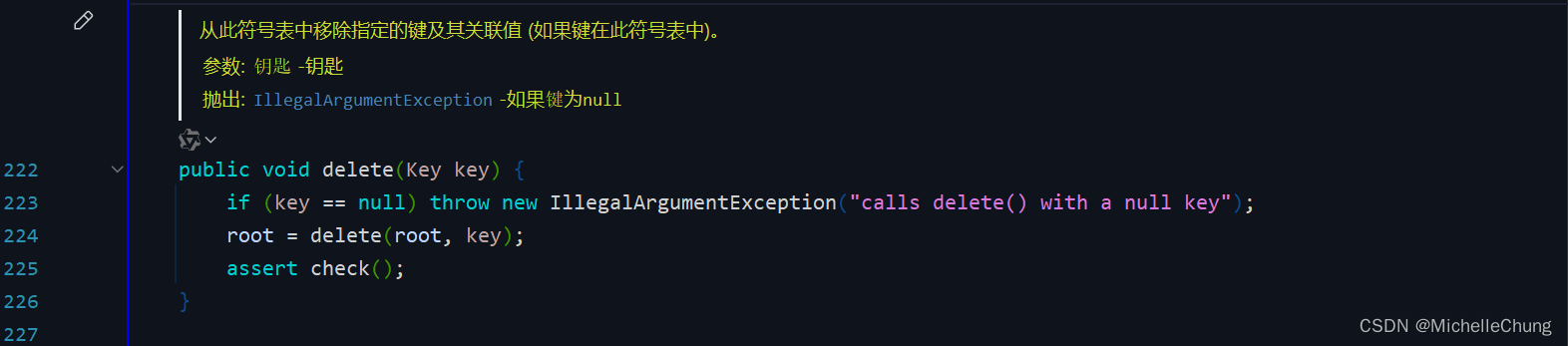
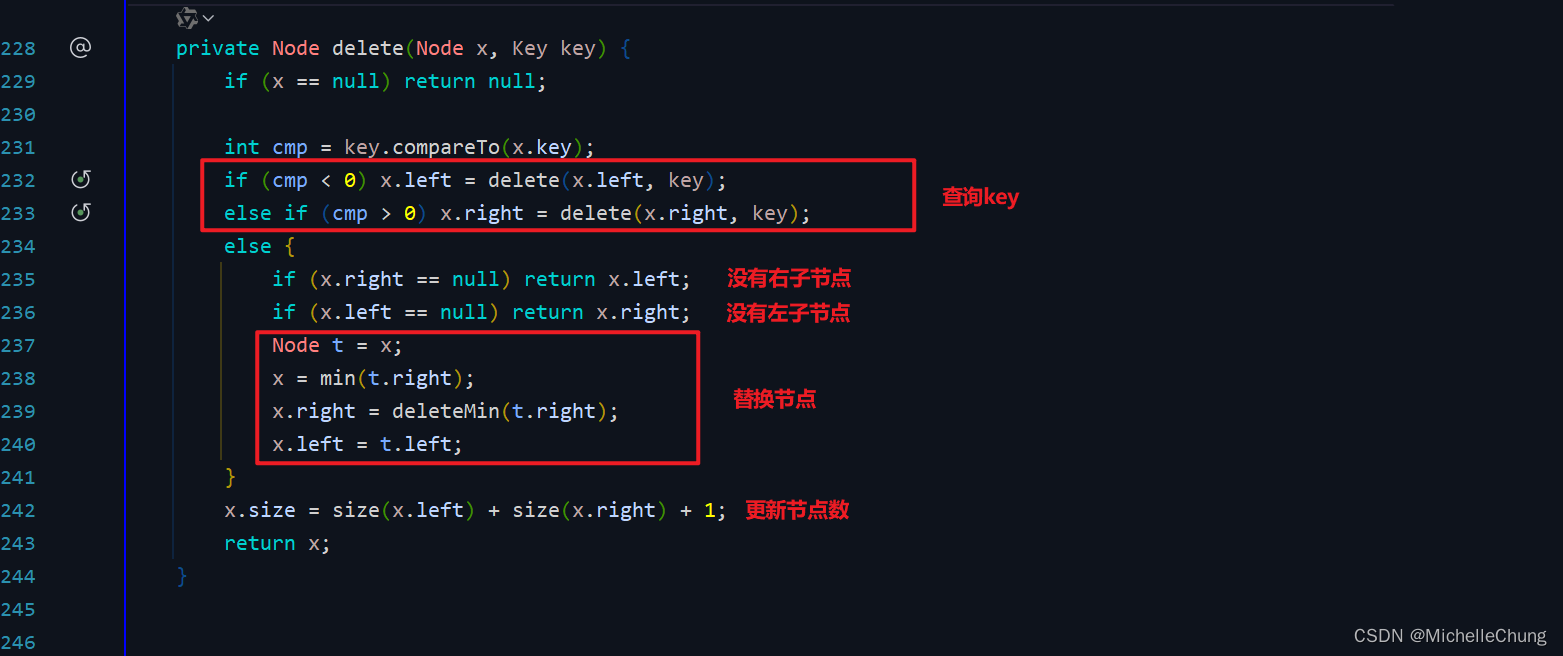
3.3:删除操作分析
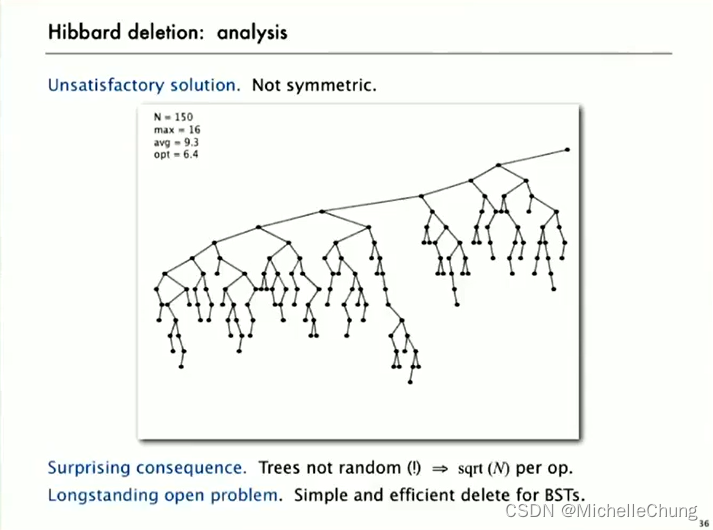
简单汉化一下:
不能令人满意的结果:不对称。
令人惊讶的事实:树不再随机 => 平方操作
长期存在的开放问题:简单高效的 BST 删除。That’s another one like merging in place, that you’d think there ought to be an easy way to do it, but in 50 years, no one’s really discovered one.
这是另一种类似原地归并的方法,你会认为应该有一种简单的方法可以做到这一点,但 50 年来,没有人真正找到解决方法。3.4:小结
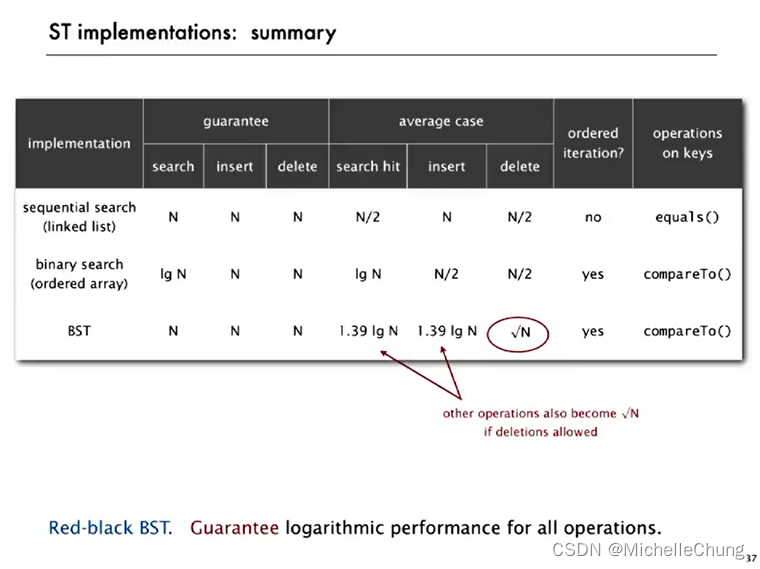
下一节:红黑二叉搜索树(Red-black BST):保证所有操作的对数性能。
But the delete operation for Binary Search Trees shows us the kind of complexity that we can encounter with working with these kinds of data structures.
BST 删除操作向我们展示了当遇到类似数据结构时我们可能遇到的复杂情况。(完)
-
相关阅读:
3GPP R17空闲态省电特性
Redis集群搭建
Iocomp ActiveX v5 SP6 带OPC -Crack
基于单片机的车载太阳能板自动跟踪系统研究
串口通信遇到的一个问题。
测试开发 | Java 接口自动化测试首选方案:REST Assured 实践
【机器学习算法】神经网络与深度学习-5 深度学习概述
Elastic:推出 7.16.2 和 6.8.22 版本的 Elasticsearch 和 Logstash 以升级 Apache Log4j2
浅谈new
桌面此电脑图标不见了的解决办法
- 原文地址:https://blog.csdn.net/Michelle_Zhong/article/details/136193904