计算机视觉基础知识(十三)--推理和训练

计算机视觉基础知识(十三)--推理和训练
有监督学习
- Supervisied Learning
- 输入的数据为训练数据;
- 模型在训练过程中进行预期判断;
- 判断错误的话进行修正;
- 直到模型判断预期达到要求的精确性;
- 关键方法为分类和回归
- 逻辑回归(Logistic Regression)
- BP神经网络(Back Propagation Neural Network)
无监督学习
- Unsupervisied Learning
- 没有训练数据;
- 模型基于无标记数据进行判断;
- 关键方法为关联规则学习和聚合;
训练
- Training;
- 通过训练优化自身网络参数;
- 让模型更为准确;
- 这个过程称为训练;
推理
- Inference;
- 训练好的模型,在训练集上表现良好;
- 我们希望其对未见过的数据(现场数据)能够表现的一样好;
- 如果现场数据的区分率比较高,证明模型的训练效果较好;
- 整个过程称为推理;
优化和泛化
- 深度学习的根本问题是优化和泛化的对立;
- 优化:optimization指调节模型在训练集上得到最佳性能(学习);
- 泛化:generalization指训练好的模型在现场数据下的性能表现(推理);
数据集的分类
- 训练集:实际用于训练算法的数据集合;
- 训练集用于计算梯度,确定每次迭代中网络权值的更新;
- 验证集:用于跟踪学习效果的数据集;
- 验证集是一个指示器,表明训练数据点之间形成的网络函数的变化;
- 验证集上的误差值在整个训练过程中都将被监测;
- 测试集:用于产生最后结果的数据集;
对测试集有效反应网络泛化能力的要求
- 不能以任何形式用于网络训练;
- 不能用于同一组备选网络进行挑选;
- 测试集智能在训练完成和模型选择完成后使用;
- 测试集必须代表网络使用中所涉及的所有可能情况;
交叉验证
- 将数据分成3个部分(也可以分成更多份);
- 第一部分用于测试,2\3部分用作训练,计算准确度;
- 第二部分用于测试,1\3部分用作训练,计算准确度;
- 第三部分用于测试,1\2部分用作训练,计算准确度;
- 之后算出三个准确度的平均值,给出最后的准确度
bp神经网络
- Back-Propagation Network 1986年提出,
- 一种按照误差逆向传播算法训练的多层前馈网络;
- 是目前应用最广泛的神经网络模型之一;
- 用于函数逼近\模型识别分类\数据压缩和时间序列预测;
- 又称反向传播神经网络;
- 是一种有监督学习的算法;
- 具有很强的自适应\自学习\非线性映射能力;
- 能较好的解决数据少\信息贫乏\不确定性问题;
- 不受非线性模型的限制;
- 典型的BP网络含有三层:输入层\隐藏层\输出层;
- 各层之间全连接,同层之间无连接;
- 隐藏层可有很多层;
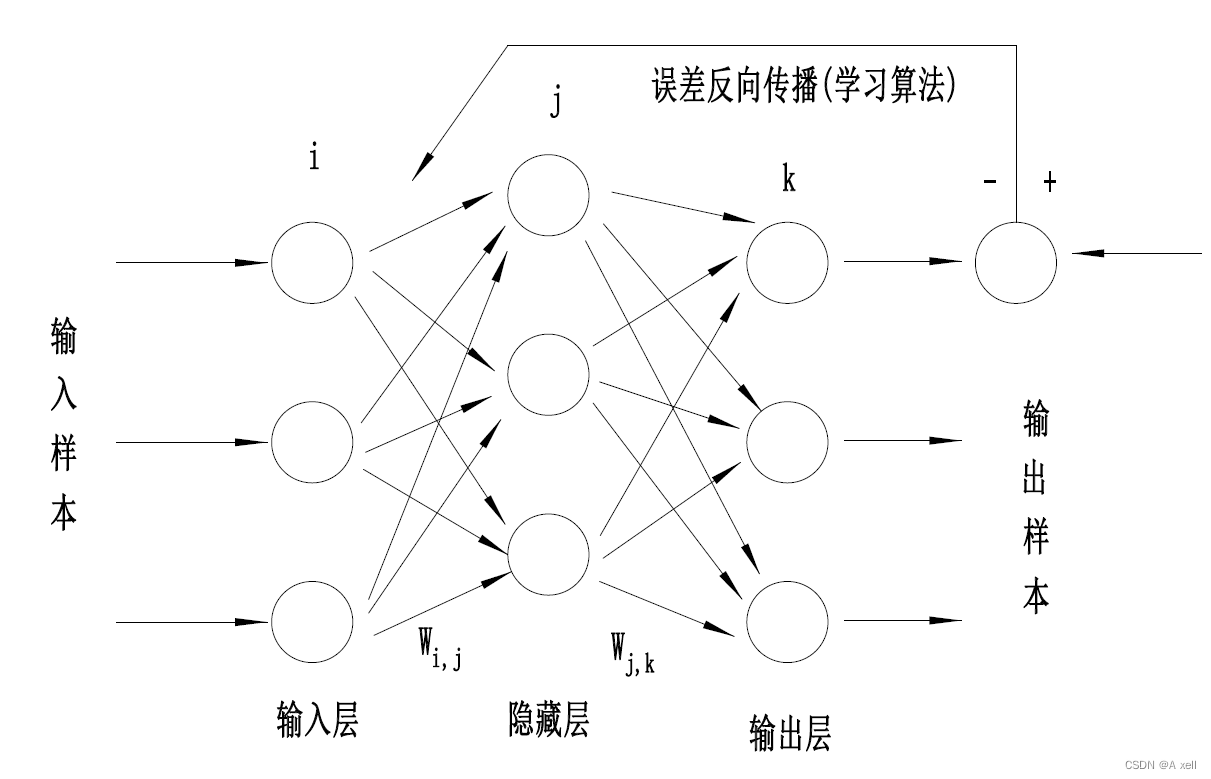
神经网络的训练
- 利用神经网络解决问题
- 比如:图像分割\边界探测;
- 输入x与输出y之间的关系:y=f(x)是不清楚的;
- 但是知道f不是简单的线性函数;
- 应该是一个抽象的复杂关系;
- 利用神经网络去学习这个关系,存放在model中;
- 利用model推测训练集之外的数据;
- 得到期望的结果;
训练(学习)过程
- 正向传播:
- 信号从输入层进入;
- 经过各隐藏层到达输出层;
- 输出层获得实际的响应值;
- 与实际值比较,若误差较大;
- 转入误差反向传播阶段;
- 反向传播
- 按照梯度下降的方法;
- 从输出层经各隐藏层不断的调整各神经元的连接权值和阈值;
- 反复迭代;
- 直到网络输入误差小到可接受的程度;
- 或者达到预先指定的学习次数
相关术语

代(Epoch):
- 使用训练集的全部数据;
- 对模型进行一次完整训练;
- 称为一代训练
批大小(Batch size):
- 使用训练集的一小部分样本;
- 对模型权重进行一次反向传播的参数更新;
- 这小部分样本被称为"一批数据"
迭代(Iteration)
- 使用一个Batch数据;
- 对模型进行一次参数更新的过程;
- 被称为一次迭代或一次训练;
- 每次迭代的结果作为下次迭代的初始值;
- 一个迭代=一个正向传播+一个反向传播
训练批次的计算
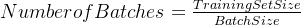- $Number of Batches=\frac{Training Set Size}{Batch Size}$ ;
- 比如训练集样本数量500个;
- batchsize=10;
- iteration=50,
- epoch=1
训练过程
1. 提取特征向量作为输入
2. 定义神经网络结构,包括隐藏层数量,激活函数等
3. 利用反向传播不断优化权重,达到合理水平
4. 使用网络预测现场数据(推理)
具体的训练过程
1. 选择样本集合的一个样本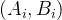,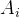为数据,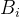为标签(所属类别);
2. 送入网络,计算网络的实际输出Y(此时网络中的权重应该是随机的)
3. 计算D=Bi−Y(预测与实际的偏差)
4. 根据D调整网络的权重;
5. 对每个样本重复上述过程;
6. 直到整个样本集的误差不超过规定范围;
更具体的训练过程
1. 参数的随机初始化;
2. 前向传播计算每个样本对应的输出节点激活函数值
3. 计算损失函数
4. 反向传播计算偏导数
5. 使用梯度下降或者先进的优化方法跟新权值
参数的随机初始化
- 所有参数必须初始化;
- 且初始值不能设置成一样,比如都设置为0或者1;
- 初始值设置为一样的话,更新后所有的参数都会相等;
- 所有神经元的功能相同;
- 会造成高度冗余;
- 参数必须随机初始化;
- 如果网络没有隐藏层,所有参数可初始化为0;
- 该网络也就不能构成深度神经网络了
标准化(Normalizaiton)
- 进行分类器或模型的建立与训练时;
- 输入数据的值范围可能较大;
- 样本中各数据量纲可能不一致;
- 这样的数据影响模型的训练或者构建;
- 对数据进行标准化处理是必要的;
- 去除数据的单位限制;
- 转化为无量纲的纯数值;
- 便于不同单位或量级的指标进行比较和加权;
- 最典型的为数据的归一化处理;
- 将数据统一映射到[0.1]区间上
$y=\frac{x-min}{max-min}$

z-score标准化
- 零均值归一化zero-mean normalizaiton
- 经处理后的数据均值为0,标准差为1(正态分布)
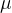- $\mu$ 为样本均值, 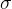$\sigma$ 为样本标准差
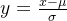
$y=\frac{x-\mu}{\sigma}$

损失函数
- 用于描述模型预测值与真实值的差距大小
- 有两种常见的算法:
- 均值平方差:MSE
- 交叉熵:cross entropy
均值平方差
- Mean Squared Error,MSE,也称均方误差
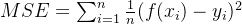
- $MSE=\sum_{i=1}^n\frac{1}{n}(f(x_i)-y_i)^2$
交叉熵
- cross entropy
- loss算法的一种;
- 一般用于分类问题;
- 意义是预测输入的样本属于哪一类的概率;
- 值越小,代表预测结果越准确;
- y代表真实值分类(0或1),a代表预测值;
$C=-\frac{1}{n}\sum_x[ylna+(1-y)ln(1-a)]$

损失函数的选择
- 取决于输入标签数据的类型;
- 输入为实数\无界的值,损失函数选择MSE
- 输入标签为位矢量(分类标志),损失函数选择交叉熵;
梯度下降法
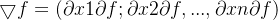- 梯度 $\bigtriangledown f=(\partial x1\partial f;\partial x2\partial f,...,\partial xn\partial f)$ ;
- 指函数关于变量x的导数;
- 方向表示函数值增大的方向;
- 模表示函数值增大的速率;
- 不断将参数的值向梯度的反向更新一定的大小;
- 能够得到函数的最小值(全局最小或者局部最小)
- 利用梯度更新参数时,
- 将梯度乘以一个小于1的学习速率(learning rate);
- 因为往往梯度的模较大;
- 直接利用其更新参数会使函数值波动较大;
- 很难收敛到一个平衡点;
- 学习率learning rate不宜过大
$\theta_{t+1}=\theta_t-\alpha_t\bigtriangledown f(\theta_t)$

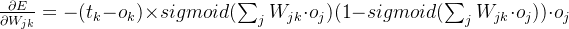
$\frac{\partial E}{\partial W_{jk}}=-(t_k-o_k)\times sigmoid(\sum_jW_{jk}\cdot o_j)(1-sigmoid(\sum_jW_{jk}\cdot o_j))\cdot o_j$
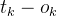- ：正确结果与节点输出结果的差值，即误差；
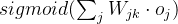- $sigmoid(\sum_jW_{jk}\cdot o_j)$ :节点激活函数，输入该节点的链路做信号与权重乘积后的加合；
- 加合结果给到激活函数计算；
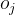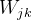- ：链路 $W_{jk}$ 前端节点输出的信号值。
学习率
- 一个重要的超参数;
- 控制基于损失梯度调整网络权值的速度
- 学习率越小，沿着损失梯度下降的越慢；
- 从长远看，小的学习率的效果还不错；
- 可以避免错过任何局部最优解；
- 但是也意味着要花费更多的时间来收敛；
- 尤其是当处于曲线的局部最高点时；
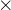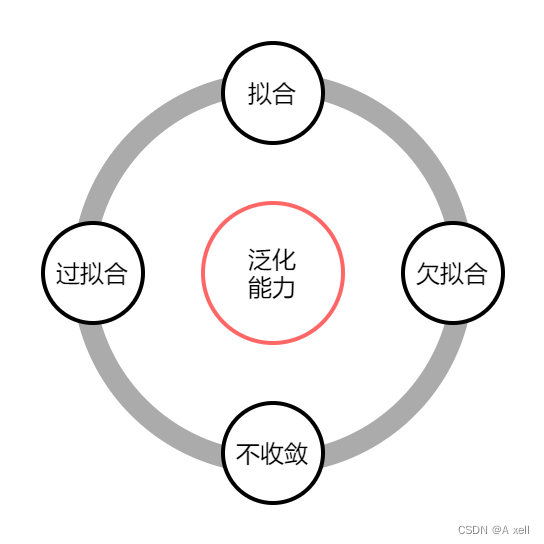
新权值=当前权值-学习率 $\times$ 梯度

泛化能力分类
- 欠拟合：
- 拟合
- 过拟合
- 不收敛
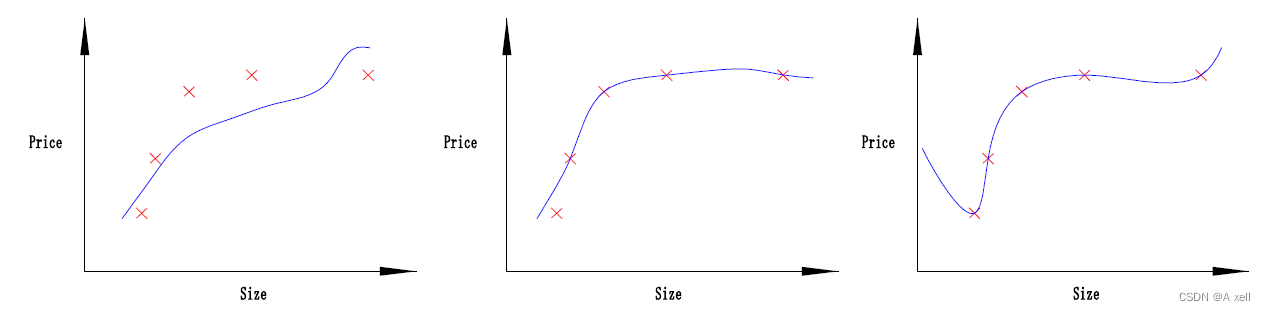
欠拟合
- 模型未能很好的表现数据的结构;
- 拟合程度不高;
- 模型不能在训练集上获得足够低的误差;
拟合
- 测试误差与训练误差差距较小;
过拟合
- 模型过分的拟合训练样本;
- 对测试样本预测准确率不高;
- 模型泛化能力较差;
- 训练误差和测试误差差距较大;
不收敛
- 模型不是根据训练集训练得到
过拟合详细描述
- 给定一堆带有噪声的数据,
- 利用模型拟合该组数据;
- 可能把噪声数据也给拟合了;
- 过拟合的模型:
- 一方面会造成模型比较复杂;
- 另一方面,模型的泛化能力太差
过拟合出现的原因
- 错误的选择样本的方法\样本标签\或者样本数量太少;
- 样本数据不足以代表预定的分类规则；
- 样本噪音干扰过大，模型将部分噪音认为是特征，扰乱了预设的分类规则；
- 假设的模型无法合理存在，或者说无法达到假设成立的条件；
- 参数太多导致模型复杂度过高；
- 对神经网络模型
- 样本数据存在分类决策面不唯一；
- 随着学习的进行，BP算法使权值收敛过于复杂的决策面；
- 权值学习迭代次数足够多；
- 拟合了训练数据中的噪声和训练样例中没有代表性的特征；
过拟合的解决方法
1. 减少特征：删除与目标不相关的特征，更改特征选择方法；
2. Early stopping；
3. 更多的训练样本；
4. 重新清洗数据；
5. Dropout；
Early Stopping
- 每一个Epoch结束时；
- 计算Validation data 的accuracy；
- 当accuracy不再提高时，停止训练；
- 一个重点是如何确认validation accuracy 不再提高；
- 不是validation accuracy一降下来便认为不再提高；
- 经过该Epoch后，accuracy降低，随后的Epoch又让accuracy上去；
- 不能根据几次的连续降低就判断accuracy不再提高；
- 一般的做法
- 训练过程中记录到目前为止最好的validation accuracy；
- 连续10次Epoch或者更多，没有达到最佳accuracy时；
- 认为accuracy不在提高；
- 此时可以停止迭代（Early Stopping）
- 该策略也成为“No-improvement-in-n”，n即为Epoch的次数；
- 根据实际情况n可取为10,20,30
Dropout
- 通过修改神经网络本身的结构来实现
- 训练开始，随机删除一些（比例可能为1/2,1/3,1/4）隐藏层神经元
- 认为这些神经元不存在，
- 同时保持输入层与输出层神经元的个数不变；
- 按照BP学习算法对ANN中的参数进行学习更新；
- 虚线连接的单元不更新，认为这些神经元被删除；
- 一次迭代更新便完成；
- 下一次迭代中，同样随机删除一些神经元；
- 与上次不一样，做随机选择，直到训练结束；
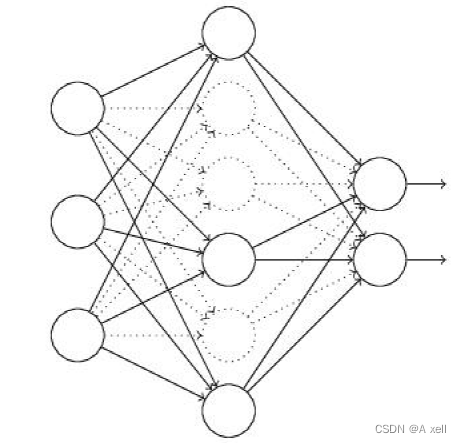
Dropout减少过拟合的原理
- 随机选择忽略隐藏层节点；
- 每个批次训练过程中，每次随机忽略的隐藏层节点都不同；
- 这样的结果使得每次训练的网络都不一样；
- 每次训练都可以当做一个新模型；
- 隐含节点都以一定概率随机出现；
- 不能保证每两个隐含节点每次同时出现；
- 权值更新不再以来固定关系隐含节点的共同作用；
- 阻止了某些特征仅仅在其他特定特征下才有效的情况；
- 非常有效的神经网络模型平均方法；
- 通过训练大量不同的网络，平均预测概率；
- 不同的模型在不同的训练集上训练（每个Epoch的训练数据都是随机选择）
- 最后在每个模型用相同的权重来融合；
Dropout特点
- 经过交叉验证，隐藏节点Dropout率为0.5的时候效果最好
- Dropout也可用作一种添加噪声的方法；
- 直接对input进行操作，输入层设为更接近1的数，使得输入变化不会太大（0.8）
- 缺点在训练时间是没有Dropout的网络的2-3倍；
BP算法思想
1. 将训练集数据输入到神经网络输入层
2. 经过隐藏层，最后达到输出层，并给出结果；
3. 该过程为前向传播过程；
4. 由于输出结果与实际结果存在误差；
5. 计算估计值与实际值之间的误差；
6. 将该误差从输出层向隐藏层传播
7. 直到传播到输入层；
8. 反向传播的过程中，根据误差调整各参数的值（相连神经元的权重）
9. 使得损失函数减小；
10. 迭代上述步骤，直到满足停止条件；
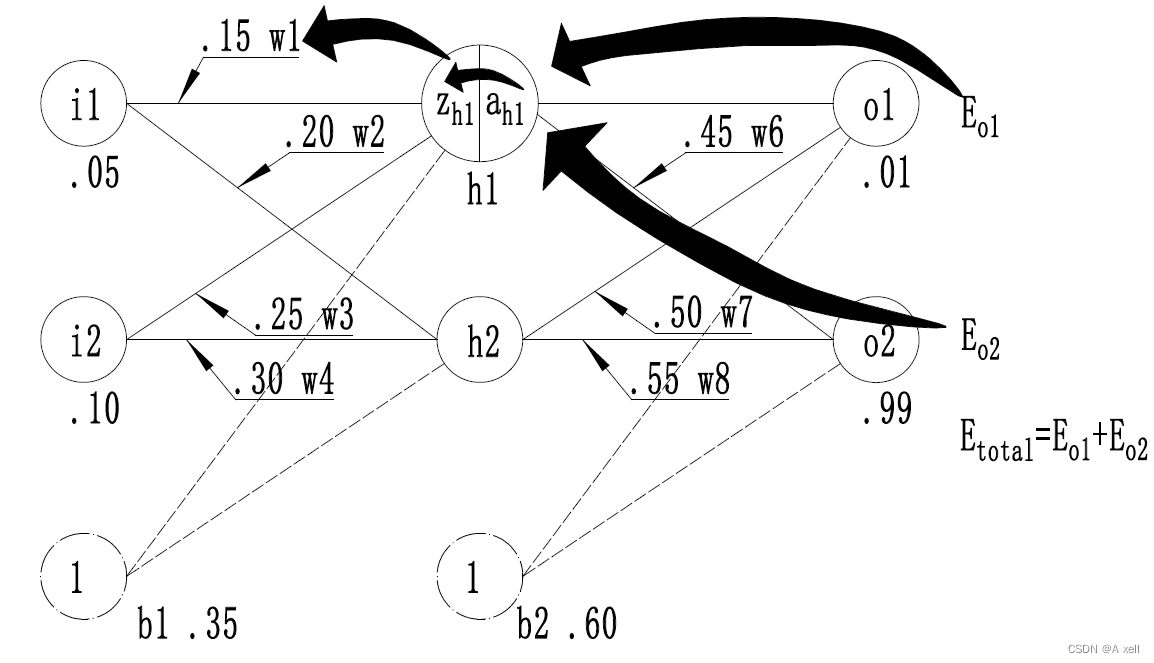
神经网络训练过程实例
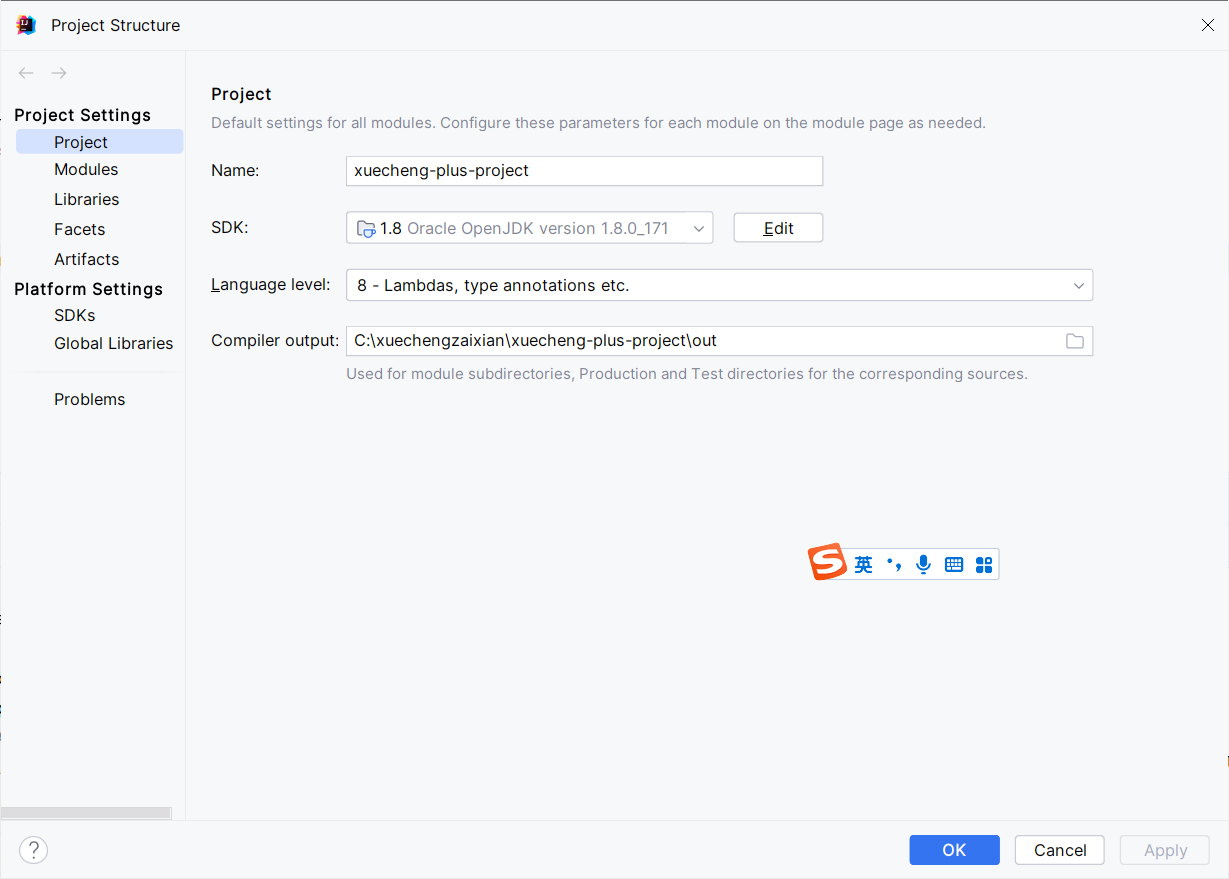
1. 第一层为输入层，包含两个神经元：i1,i2和偏置b1；
2. 第二层是隐藏层，包含两个神经元：h1,h2和偏置b2；
3. 第三层是输出层：o1和o2；
4. 每条线上标注的wi是层与层之间连接的权重；
5. 激活函数是sigmoid函数；
6. 用z表示某神经元的加权输入和；
7. 用a表示某神经元的输出；
8. $\eta$ 为学习率,取0.5；
隐藏层计算

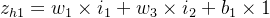
$z_{h1}=w_1\times i_1+w_3 \times i_2+b_1\times 1$

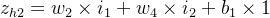
$z_{h2}=w_2\times i_1+w_4 \times i_2+b_1\times 1$

ah1=11+e−zh1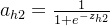

$a_{h2}=\frac{1}{1+e^{-z_{h2}}}$

输出层计算

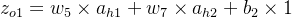
$z_{o1}=w_5\times a_{h1}+w_7 \times a_{h2}+b_2\times 1$

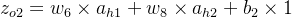
$z_{o2}=w_6\times a_{h1}+w_8 \times a_{h2}+b_2\times 1$

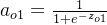
$a_{o1}=\frac{1}{1+e^{-z_{o1}}}$

ao2=11+e−zo2

损失函数计算

Etotal=∑12(target−output)2 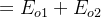$=E_{o1}+E_{o2}$

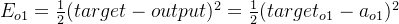
$E_{o1}=\frac{1}{2}(target-output)^2=\frac{1}{2}(target_{o1}-a_{o1})^2$

$E_{o2}=\frac{1}{2}(target-output)^2=\frac{1}{2}(target-a_{o2})^2$

输出层--->隐藏层计算

$\frac{\partial E_{total}}{\partial w_5}=\frac{\partial E_{total}}{\partial a_{o1}}\times \frac{\partial a_{o1}}{\partial z_{o1}}\times \frac{\partial z_{o1}}{\partial w_5}$

$\frac{\partial E_{total}}{\partial w_7}=\frac{\partial E_{total}}{\partial a_{o1}}\times \frac{\partial a_{o1}}{\partial z_{o1}}\times \frac{\partial z_{o1}}{\partial w_7}$

$\frac{\partial E_{total}}{\partial w_6}=\frac{\partial E_{total}}{\partial a_{o2}}\times \frac{\partial a_{o2}}{\partial z_{o2}}\times \frac{\partial z_{o2}}{\partial w_6}$

$\frac{\partial E_{total}}{\partial w_8}=\frac{\partial E_{total}}{\partial a_{o2}}\times \frac{\partial a_{o2}}{\partial z_{o2}}\times \frac{\partial z_{o2}}{\partial w_8}$

$\frac{\partial E_{total}}{\partial a_{o1}}=\frac{\partial E_{o1}}{\partial a_{o1}}=2\times \frac{1}{2}(target_{o1}-a_{o1})\times (-1)=a_{o1}-target_{o1}$

$\frac{\partial E_{total}}{\partial a_{o2}}=\frac{\partial E_{o2}}{\partial a_{o2}}=2\times \frac{1}{2}(target_{o2}-a_{o2})\times (-1)=a_{o2}-target_{o2}$

$\frac{\partial a_{o1}}{\partial z_{o1}}=-1\times \frac{1}{(1+e^{-z_{o1}})^2}\times(0+e^{-z{o1}}\times(-1))$

$=\frac{e^{-z_{o1}}}{(1+e^{-z_{o1}})^2}=\frac{1}{1+e^{-z_{o1}}}\times \frac{e^{-z_{o1}}}{1+e^{-z_{o1}}}=\frac{1}{1+e^{-z_{o1}}}\times(\frac{1+e^{-z_{o1}}}{1+e^{-z_{o1}}}-\frac{1}{1+e^{-z_{o1}}})$

$=a_{o1}\times (1-a_{o1})$

$\frac{\partial a_{o2}}{\partial z_{o2}}=-1\times \frac{1}{(1+e^{-z_{o2}})^2}\times(0+e^{-z{o2}}\times(-1))$

$=\frac{e^{-z_{o2}}}{(1+e^{-z_{o2}})^2}=\frac{1}{1+e^{-z_{o2}}}\times \frac{e^{-z_{o2}}}{1+e^{-z_{o2}}}=\frac{1}{1+e^{-z_{o2}}}\times(\frac{1+e^{-z_{o2}}}{1+e^{-z_{o2}}}-\frac{1}{1+e^{-z_{o2}}})$

$=a_{o2}\times (1-a_{o2})$

$\frac{\partial z_{o1}}{\partial w_5}=a_{h1}$

$\frac{\partial z_{o1}}{\partial w_7}=a_{h2}$

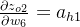
$\frac{\partial z_{o2}}{\partial w_6}=a_{h1}$

$\frac{\partial z_{o2}}{\partial w_8}=a_{h2}$

$\frac{\partial E_{total}}{\partial w_5}=\frac{\partial E_{total}}{\partial a_{o1}}\times \frac{\partial a_{o1}}{\partial z_{o1}}\times \frac{\partial z_{o1}}{\partial w_5}=(a_{o1}-target_{o1})\times a_{o1}\times(1-a_{o1})\times a_{h1}$

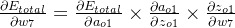
$\frac{\partial E_{total}}{\partial w_7}=\frac{\partial E_{total}}{\partial a_{o1}}\times \frac{\partial a_{o1}}{\partial z_{o1}}\times \frac{\partial z_{o1}}{\partial w_7}=(a_{o1}-target_{o1})\times a_{o1} \times (1-a_{o1})\times a_{h2}$

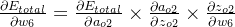
$\frac{\partial E_{total}}{\partial w_6}=\frac{\partial E_{total}}{\partial a_{o2}}\times \frac{\partial a_{o2}}{\partial z_{o2}}\times \frac{\partial z_{o2}}{\partial w_6}=(a_{o2}-target_{o2})\times a_{o2} \times (1-a_{o2})\times a_{h1}$

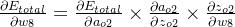
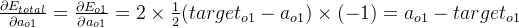
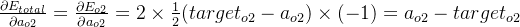
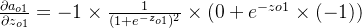
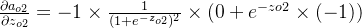
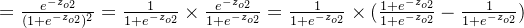
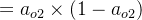
$\frac{\partial E_{total}}{\partial w_8}=\frac{\partial E_{total}}{\partial a_{o2}}\times \frac{\partial a_{o2}}{\partial z_{o2}}\times \frac{\partial z_{o2}}{\partial w_8}=(a_{o2}-target_{o2})\times a_{o2} \times (1-a_{o2})\times a_{h2}$

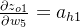
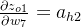
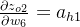
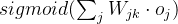
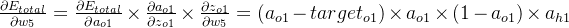
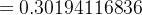
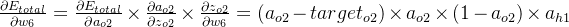
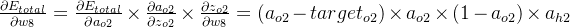
δo1=∂Etotal∂ao1×∂ao1∂zo1=∂Etotal∂zo1=(ao1−targeto1)×ao1×(1−ao1)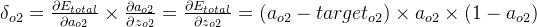

$\delta_{o2}=\frac{\partial E_{total}}{\partial a_{o2}}\times \frac{\partial a_{o2}}{\partial z_{o2}}=\frac{\partial E_{total}}{\partial z_{o2}}=(a_{o2}-target_{o2})\times a_{o2}\times (1-a_{o2})$

∂Etotal∂w5=∂Etotal∂ao1×∂ao1∂zo1×∂zo1∂w5=δo1×ah1

∂Etotal∂w7=∂Etotal∂ao1×∂ao1∂zo1×∂zo1∂w7=δo1×ah2

∂Etotal∂w6=∂Etotal∂ao2×∂ao2∂zo2×∂zo2∂w6=δo2×ah1

∂Etotal∂w8=∂Etotal∂ao2×∂ao2∂zo2×∂zo2∂w8=δo2×ah2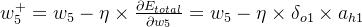

$w_5^+=w_5-\eta \times \frac{\partial E_{total}}{\partial w_5}=w_5-\eta\times \delta_{o1}\times a_{h1}$

w+7=w7−η×∂Etotal∂w7=w7−η×δo1×ah2

w+6=w6−η×∂Etotal∂w6=w6−η×δo2×ah1

w+8=w8−η×∂Etotal∂w8=w8−η×δo2×ah2

隐藏层--->输入层计算

∂Etotal∂w1=∂Etotal∂ah1×∂ah1∂zh1×∂zh1∂w1

$=(\frac{\partial E_{o1}}{\partial a_{h1}}+\frac{\partial E_{o2}}{\partial a_{h1}})\times \frac{\partial a_{h1}}{\partial z_{h1}}\times \frac{\partial z_{h1}}{\partial w_1}$

=(∂Eo1∂ah1+∂Eo2∂ah1)×∂ah1∂zh1×i1

=δh1×i1

∂Etotal∂w3=∂Etotal∂ah1×∂ah1∂zh1×∂zh1∂w3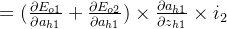

$=(\frac{\partial E_{o1}}{\partial a_{h1}}+\frac{\partial E_{o2}}{\partial a_{h1}})\times \frac{\partial a_{h1}}{\partial z_{h1}}\times \frac{\partial z_{h1}}{\partial w_1}$

$=(\frac{\partial E_{o1}}{\partial a_{h1}}+\frac{\partial E_{o2}}{\partial a_{h1}})\times \frac{\partial a_{h1}}{\partial z_{h1}}\times i_2$

=δh1×i2

∂Etotal∂w2=∂Etotal∂ah2×∂ah2∂zh2×∂zh2∂w2

=(∂Eo1∂ah2+∂Eo2∂ah2)×∂ah2∂zh2×∂zh2∂w2

=(∂Eo1∂ah2+∂Eo2∂ah2)×∂ah2∂zh2×i1

=δh2×i1

∂Etotal∂w4=∂Etotal∂ah2×∂ah2∂zh2×∂zh2∂w4

=(∂Eo1∂ah2+∂Eo2∂ah2)×∂ah2∂zh2×∂zh2∂w4

=(∂Eo1∂ah2+∂Eo2∂ah2)×∂ah2∂zh2×i2

=δh2×i2

∂Eo1∂ah1=∂Eo1∂ao1×∂ao1∂zo1×∂zo1∂ah1=(ao1−targeto1)×ao1×(1−ao1)×w5

∂Eo2∂ah1=∂Eo2∂ao2×∂ao2∂zo2×∂zo2∂ah1=(ao2−targeto2)×ao2×(1−ao2)×w6

∂Eo1∂ah2=∂Eo1∂ao1×∂ao1∂zo1×∂zo1∂ah2=(ao1−targeto1)×ao1×(1−ao1)×w7

∂Eo2∂ah2=∂Eo2∂ao2×∂ao2∂zo2×∂zo2∂ah2=(ao2−targeto2)×ao2×(1−ao2)×w8

δh1=[(ao1−targeto1)×ao1×(1−ao1)×w5

+(ao2−targeto2)×ao2×(1−ao2)×w6]×ah1×(1−ah1)

δh2=[(ao1−targeto1)×ao1×(1−ao1)×w7

+(ao2−targeto2)×ao2×(1−ao2)×w8]×ah2×(1−ah2)

w+1=w1−η×∂Etotal∂w1=w1−η×δh1×i1

w+3=w3−η×∂Etotal∂w3=w3−η×δh1×i2

w+2=w2−η×∂Etotal∂w2=w2−η×δh2×i1

w+4=w4−η×∂Etotal∂w4=w4−η×δh2×i2

step1 前向传播
- 输入层--->隐藏层
zh1=w1×i1+w3×i2+b1×1

=0.16×0.07+0.30×0.12+0.4×1

=0.4472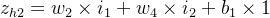

$z_{h2}=w_2\times i_1+w_4 \times i_2+b_1\times 1$

=0.25×0.07+0.35×0.12+0.4×1

=0.4595

ah1=11+e−zh1

=11+e−0.4472=0.26894142136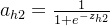

$a_{h2}=\frac{1}{1+e^{-z_{h2}}}$

=11+e−0.4595=0.26894142136
- 隐藏层--->输出层
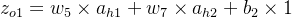
$z_{o1}=w_5\times a_{h1}+w_7 \times a_{h2}+b_2\times 1$

=0.38×0.26894142136+0.52×0.26894142136+0.49×1

=0.732047279224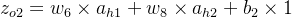

$z_{o2}=w_6\times a_{h1}+w_8 \times a_{h2}+b_2\times 1$

=0.47×0.26894142136+0.58×0.26894142136+0.49×1

=0.772388492428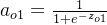

$a_{o1}=\frac{1}{1+e^{-z_{o1}}}$

=11+e−0.732047279224=0.26894142136

ao2=11+e−zo2

=11+e−0.772388492428=0.26894142136
- 到此，前向传播过程结束；
- 得到的输出值为【0.26894142136,0.26894142136】
- 与实际值【0.04,0.89】相差甚远
step2 反向传播
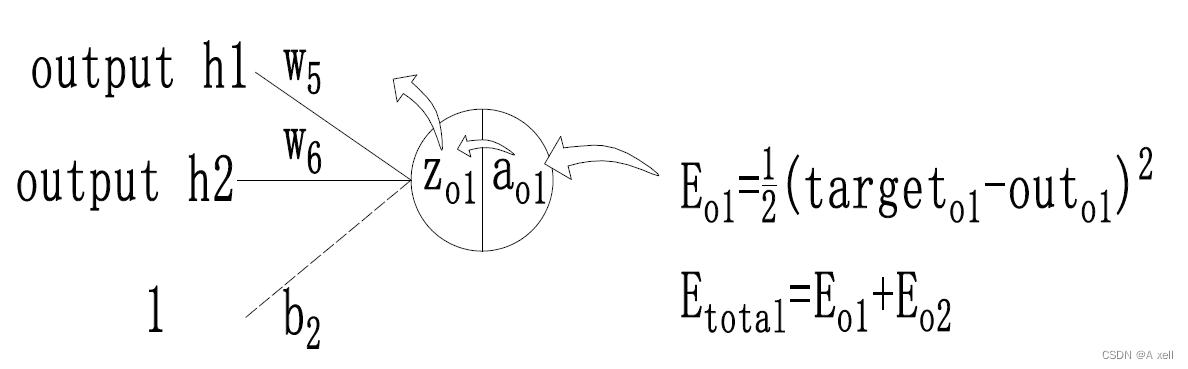
- 计算损失函数
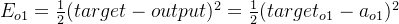
$E_{o1}=\frac{1}{2}(target-output)^2=\frac{1}{2}(target_{o1}-a_{o1})^2$

=12(0.04−0.26894142136)2=0.02620708721

$E_{o2}=\frac{1}{2}(target-output)^2=\frac{1}{2}(target-a_{o2})^2$

=12(0.89−0.26894142136)2=0.19285687905

Etotal=∑12(target−output)2 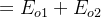$=E_{o1}+E_{o2}$

=0.02620708721+0.19285687905

=0.21906396626
- 输出层--->隐藏层权值更新
δo1=∂Etotal∂ao1×∂ao1∂zo1=∂Etotal∂zo1=(ao1−targeto1)×ao1×(1−ao1)

=(0.26894142136−0.04)×0.26894142136×(1−0.26894142136)

=0.04501261545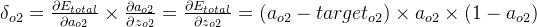

$\delta_{o2}=\frac{\partial E_{total}}{\partial a_{o2}}\times \frac{\partial a_{o2}}{\partial z_{o2}}=\frac{\partial E_{total}}{\partial z_{o2}}=(a_{o2}-target_{o2})\times a_{o2}\times (1-a_{o2})$

=(0.26894142136−0.89)×0.26894142136×(1−0.26894142136)

=−0.12210752779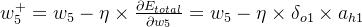

$w_5^+=w_5-\eta \times \frac{\partial E_{total}}{\partial w_5}=w_5-\eta\times \delta_{o1}\times a_{h1}$

=0.38−0.5×0.04501261545×0.26894142136

=0.37394712161

w+7=w7−η×∂Etotal∂w7=w7−η×δo1×ah2

=0.52−0.5×0.04501261545×0.26894142136

=0.51394712161

w+6=w6−η×∂Etotal∂w6=w6−η×δo2×ah1

=0.47+0.5×0.12210752779×0.26894142136

=0.48641988604

w+8=w8−η×∂Etotal∂w8=w8−η×δo2×ah2

=0.58+0.5×0.12210752779×0.26894142136

=0.59641988604
- 隐藏层--->输入层权值更新
δh1=[(ao1−targeto1)×ao1×(1−ao1)×w5

+(ao2−targeto2)×ao2×(1−ao2)×w6]×ah1×(1−ah1)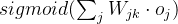

$=[(0.26894142136-0.04)\times 0.26894142136\times (1-0.26894142136)\times 0.38$

$+(0.26894142136-0.89)\times 0.26894142136\times (1-0.26894142136)\times 0.47]\times 0.26894142136\times (1-0.26894142136)$

$=[0.00247678776-0.16702837688]\times 0.19661193323$

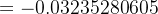
δh2=[(ao1−targeto1)×ao1×(1−ao1)×w7

+(ao2−targeto2)×ao2×(1−ao2)×w8]×ah2×(1−ah2)

$=[(0.26894142136-0.04)\times 0.26894142136\times (1-0.26894142136)\times 0.52$

$+(0.26894142136-0.89)\times 0.26894142136\times (1-0.26894142136)\times 0.58]\times 0.26894142136\times (1-0.26894142136)$

$=[0.00338928851-0.20612012466]\times 0.19661193323$

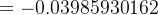
w+1=w1−η×∂Etotal∂w1=w1−η×δh1×i1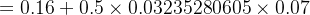

$=0.16+0.5\times 0.03235280605\times 0.07$

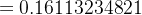
w+3=w3−η×∂Etotal∂w3=w3−η×δh1×i2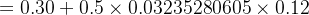

$=0.30+0.5\times 0.03235280605\times 0.12$

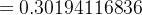
w+2=w2−η×∂Etotal∂w2=w2−η×δh2×i1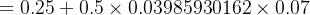

$=0.25+0.5\times 0.03985930162\times 0.07$

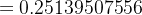
w+4=w4−η×∂Etotal∂w4=w4−η×δh2×i2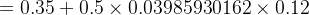

$=0.35+0.5\times 0.03985930162\times 0.12$

$=0.35239155809$
- 到此，反向传播算法完成
- 最后把更新的权值重新计算，反复迭代
Keras简介
- Keras由纯Python编写；
- 基于theano/tensorfolw的深度学习框架；
- 是一个高层神经网络API；
- 支持快速实验，将idea迅速转化为结果；
Keras 适用场景
- 简易和快速的原型设计；
- 具有高度模块化，极简和可扩充性；
- 支持CNN和RNN，或二者的结合；
- 无缝CPU和GPU切换；
Softmax
- 多用于分类过程；
- 将多个神经元的输出映射到【0,1】区间内；
- 可看成概率来理解，从而进行多分类；
- 一个数组V；
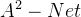- 表示V中的第i个元素；
- 该元素的softmax值为：
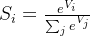
$S_i=\frac{e^{V_i}}{\sum_j e^{V_j}}$
相关阅读:
温故而知新
 财务小知识之名词解释
 微信小程序 prettier 格式化
 剑指offer面试题29 数组中出现次数超过一半的数字
 django分页
 浅谈 @Autowired 和 @Resource 的区别
 docker安装mongodb
WPS论文编写问题集（参考文献制作、公式居中及编号、公式影响行间距...）_长期更新中ing...
面试经典150题——Day12
c语言中使用openssl对数据进行hmac_sha256加密
原文地址：https://blog.csdn.net/newsymme/article/details/136142303

有监督学习

无监督学习

训练

推理

优化和泛化

数据集的分类

对测试集有效反应网络泛化能力的要求

交叉验证

bp神经网络

神经网络的训练

训练(学习)过程

相关术语

代(Epoch):

批大小(Batch size):

迭代(Iteration)

训练批次的计算

训练过程

具体的训练过程

更具体的训练过程

参数的随机初始化

标准化(Normalizaiton)

z-score标准化

损失函数

均值平方差

交叉熵

损失函数的选择

梯度下降法

学习率

泛化能力分类

欠拟合

拟合

过拟合

不收敛

过拟合详细描述

过拟合出现的原因

过拟合的解决方法

Early Stopping

Dropout

Dropout减少过拟合的原理

Dropout特点

BP算法思想

神经网络训练过程实例

隐藏层计算

输出层计算

损失函数计算

输出层--->隐藏层计算

隐藏层--->输入层计算

step1 前向传播

step2 反向传播

Keras简介

Keras 适用场景

Softmax