【leetcode】深搜、暴搜、回溯、剪枝（C++）2

---

一、括号生成

1、题目描述

leetcode链接

2、代码

class Solution 
{
public:
    // 1、全局变量
    string path;
    vector<string> ret;
    int right = 0, left = 0, n = 0;
    vector<string> generateParenthesis(int _n) 
    {
        n = _n;
        dfs();
        return ret;
    }
    void dfs()
    {
        // 1、出口
        if(right == n)
        {
            ret.push_back(path);
            return;
        }
        // 2、添加左括号
        if(left < n)
        {
            path.push_back('(');
            left++;
            dfs();
            path.pop_back(); // 恢复现场
            left--;
        }
        if(right < left) // 3、添加右括号
        {
            path.push_back(')');
            right++;
            dfs();
            path.pop_back(); // 恢复现场
            right--;
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

3、解析

二、组合

1、题目描述

leetcode链接

2、代码

class Solution 
{
public:
    // 1、全局变量
    int n = 0; // 1-n
    int k = 0; // 几个数
    vector<int> path; // 路径
    vector<vector<int>> ret; // 增加的路径函数
    vector<vector<int>> combine(int _n, int _k) 
    {
        n = _n;
        k = _k;
        dfs(1); // 2、dfs
        return ret;
    }
    void dfs(int _pos)
    {
        // 1、函数递归出口
        if(path.size() == k)
        {
            ret.push_back(path);
            return;
        }
        // 2、遍历--剪枝
        for(int pos = _pos; pos <= n; pos++)
        {
            path.push_back(pos);
            dfs(pos + 1); // pos下一个数进行递归实现剪枝
            path.pop_back(); // 回溯--恢复现场         
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

3、解析

三、目标和

1、题目描述

leetcode链接

2、代码

全局变量的超时代码：
原因在于nums的长度最长有20，其2^20次方太大了。但是leetcode居然通过了。

class Solution 
{
public:
    // 1、全局变量
    int ret; // 返回
    int aim; // 目标值
    int path; // 路径
    int findTargetSumWays(vector<int>& nums, int target) 
    {
        aim = target;
        dfs(nums, 0);
        return ret;
    }
    void dfs(vector<int>& nums, int pos)
    {
        // 1、递归出口
        if(pos == nums.size())
        {
            if(path == aim)
            {
                ret++;
            }
            return;
        }
        // 2、加法
        path += nums[pos];
        dfs(nums, pos + 1);
        path -= nums[pos]; // 恢复现场
        // 3、减法
        path -= nums[pos];
        dfs(nums, pos + 1);
        path += nums[pos]; // 恢复现场
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

path作为参数的正确代码：

class Solution 
{
public:
    // 1、全局变量
    int ret; // 返回
    int aim; // 目标值
    int findTargetSumWays(vector<int>& nums, int target) 
    {
        aim = target;
        dfs(nums, 0, 0);
        return ret;
    }
    void dfs(vector<int>& nums, int pos, int path)
    {
        // 1、递归出口
        if(pos == nums.size())
        {
            if(path == aim)
            {
                ret++;
            }
            return;
        }
        // 2、加法
        path += nums[pos];
        dfs(nums, pos + 1, path);
        path -= nums[pos]; // 恢复现场
        // 3、减法
        path -= nums[pos];
        dfs(nums, pos + 1, path);
        path += nums[pos]; // 恢复现场
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

3、解析

四、组合总和

1、题目描述

leetcode链接

2、代码

解法一：

class Solution 
{
public:
    // 1、全局变量
    vector<vector<int>> ret; // 返回
    vector<int> path; // 路径
    int aim; // 记录target
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) 
    {
        aim = target;
        dfs(candidates, 0, 0);
        return ret;
    }
    void dfs(vector<int>& nums, int pos, int sum)
    {
        // 1、递归出口
        if(sum == aim)
        {
            ret.push_back(path);
            return;
        }
        if(sum > aim)
        {
            return;
        }
        // 循环
        for(int i = pos; i < nums.size(); i++)
        {
            path.push_back(nums[i]);
            sum += nums[i];
            dfs(nums, i, sum); // 还是从开始
            path.pop_back(); // 恢复现场
            sum -= nums[i];
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

解法二：

class Solution 
{
public:
    // 1、全局变量
    vector<vector<int>> ret; // 返回
    vector<int> path; // 路径
    int aim; // 记录target
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) 
    {
        aim = target;
        dfs(candidates, 0, 0);
        return ret;
    }
    void dfs(vector<int>& nums, int pos, int sum)
    {
        // 1、递归出口
        if(sum == aim)
        {
            ret.push_back(path);
            return;
        }
        if(sum > aim || pos == nums.size())
        {
            return;
        }
        // 循环
        for(int k = 0; k * nums[pos] + sum <= aim; k++)
        {
            if(k)
            {
                path.push_back(nums[pos]);
            }
            dfs(nums, pos + 1, sum + k * nums[pos]);
        }
        // 恢复现场
        for(int k = 1; k * nums[pos] + sum <= aim; k++)
        {
            path.pop_back();
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

3、解析

解法一：

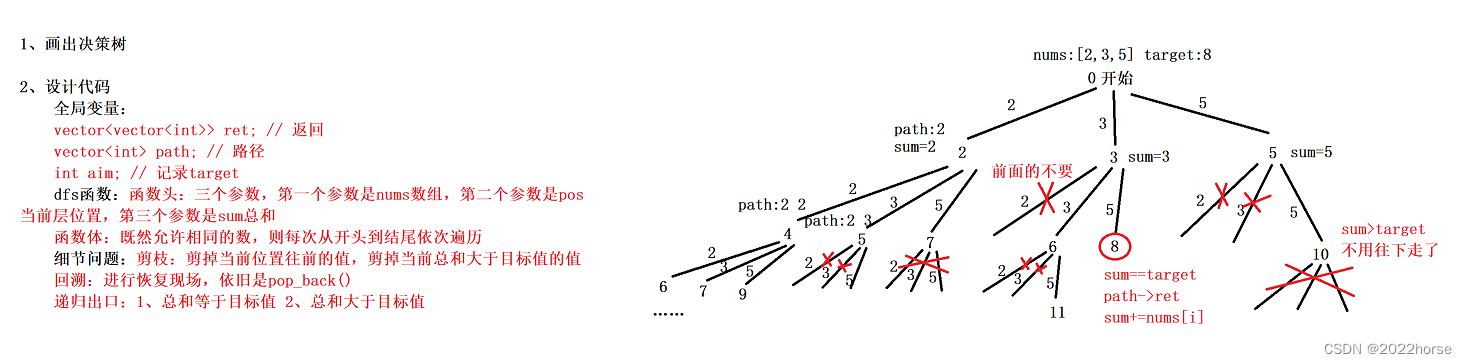
解法二：

五、字母大小写全排列

1、题目描述

leetcode链接

2、代码

class Solution 
{
public:
    // 全局变量
    string path; // 路径
    vector<string> ret; // 返回
    vector<string> letterCasePermutation(string s) 
    {
        dfs(s, 0); // 将s这个字符串的第0个位置进行传参
        return ret;
    }
    void dfs(string s, int pos)
    {
        // 递归出口
        if(pos == s.length())
        {
            ret.push_back(path);
            return;
        }
        // 先记录一下当前的字母
        char ch = s[pos];
        // 不改变
        path.push_back(ch);
        dfs(s, pos + 1);
        path.pop_back(); // 恢复现场
        // 改变
        if(ch < '0' || ch > '9')
        {
            // 进行改变大小写函数
            ch = Change(ch);
            path.push_back(ch);
            dfs(s, pos + 1); // 往下一层递归
            path.pop_back(); // 恢复现场
        }
    }
    char Change(char ch)
    {
        if(ch >= 'a' && ch <= 'z')
        {
            ch -= 32;
        }
        else
        {
            ch += 32;
        }
        return ch;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

3、解析

六、优美的排列

1、题目描述

leetcode链接

2、代码

class Solution 
{
public:
    // 全局变量
    int ret; // 返回
    bool check[16]; // 判断相对应位置是true还是false
    int countArrangement(int n) 
    {
        dfs(1, n); // 下标从1开始
        return ret;
    }
    void dfs(int pos, int n)
    {
        // 递归出口
        if(pos == n + 1) // 因为是从1开始的
        {
            ret++; // 只用做数的统计即可
            return;
        }
        // 循环
        for(int i = 1; i <= n; i++)
        {
            if(check[i] == false && (pos % i == 0 || i % pos == 0))
            {
                check[i] = true; // 表示用了
                dfs(pos + 1, n); // 递归到下一层
                check[i] = false; // 恢复现场
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

3、解析

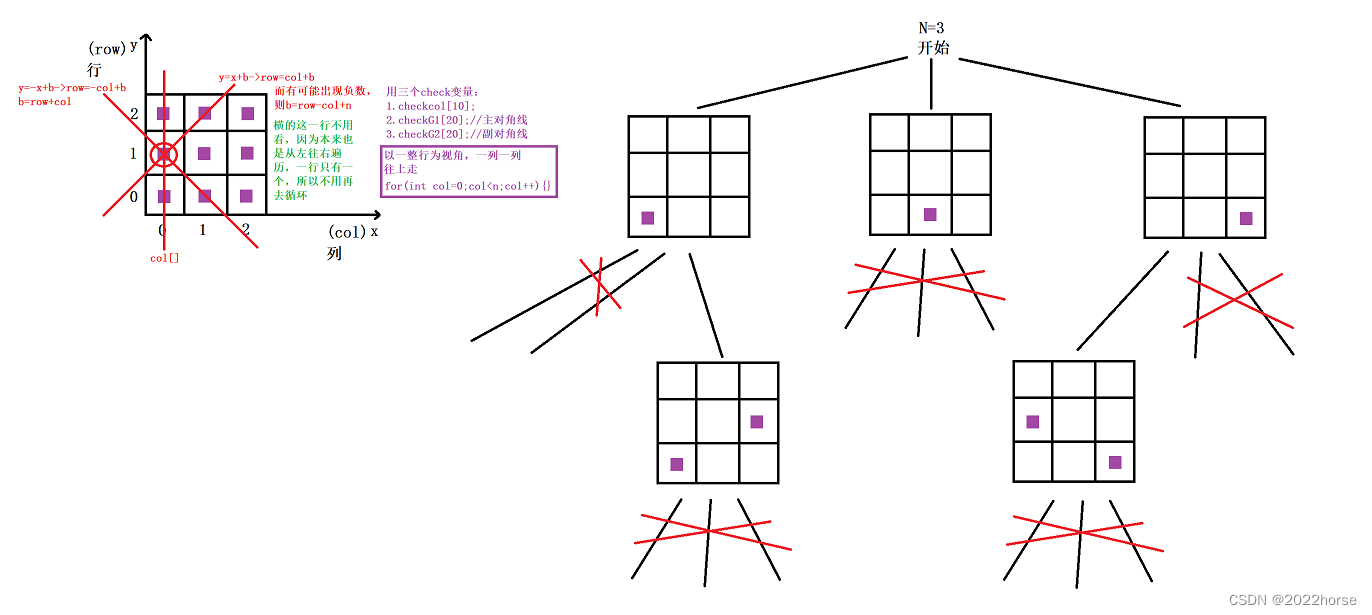
七、N皇后

1、题目描述

leetcode链接

2、代码

class Solution 
{
public:
    // 全局变量
    bool checkcol[10]; // 列
    bool checkG1[20]; // 主对角线
    bool checkG2[20]; // 副对角线
    vector<string> path; // 路径
    vector<vector<string>> ret; // 返回
    int n; // 全局变量n
    vector<vector<string>> solveNQueens(int _n) 
    {
        n = _n;
        // 初始化棋盘
        path.resize(n);
        for(int i = 0; i < n; i++)
        {
            path[i].append(n, '.');
        }
        dfs(0);
        return ret;
    }
    void dfs(int row) // 行
    {
        // 递归出口
        if(row == n)
        {
            ret.push_back(path);
            return;
        }
        for(int col = 0; col < n; col++) // 每一行所在的列位置
        {
            if(checkcol[col] == false/*一整列*/ && checkG1[row - col + n] == false/*y-x+n*/ && checkG2[row + col] == false/*y+x*/) // 判断条件进入
            {
                path[row][col] = 'Q';
                checkcol[col] = checkG1[row - col + n] = checkG2[row + col] = true;
                dfs(row + 1);
                // 恢复现场
                path[row][col] = '.';
                checkcol[col] = checkG1[row - col + n] = checkG2[row + col] = false;
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

3、解析

这里我们着重在剪枝方面上面的讲解，我们重点需要明白N皇后剪枝的作用，因为皇后是能吃横的一整行，竖的一整列，主对角线和副对角线一整个，这里原本是要循环四次，但是我们经过想法发现其实只需要判断三个位置即可，第一个位置是竖着的，第二个位置是主对角线，第三个位置是副对角线，因为横着的一行是不需要进行判断的，因为我们的思路是以一整行为一个视角，从左往右依次填的！我们根据简单的数学原理，主对角线是y=x+b的，而由于会出现负数情况，我们左右两边各加一个n即可，我们此时b就为：y-x+n。我们副对角线是y=-x+b，我们的b为y+x即可！那我们接下来的思路画出决策树以后只需要考虑回溯的问题，我们恢复现场只需要将用过的全部变成没用过的即可。

八、有效的数独

1、题目描述

leetcode链接

2、代码

class Solution 
{
public:
    // 全局变量
    bool row[9][10]; // 行坐标加值
    bool col[9][10]; // 列坐标加值
    bool grid[3][3][10]; // 棋盘坐标加值
    bool isValidSudoku(vector<vector<char>>& board) 
    {
        for(int i = 0; i < 9; i++) // 行
        {
            for(int j = 0; j < 9; j++) // 列
            {
                if(board[i][j] != '.') // 数字的时候
                {
                    int num = board[i][j] - '0'; // 记录一下数
                    if(row[i][num] == true || col[j][num] == true || grid[i / 3][j / 3][num] == true)
                    {
                        return false;
                    }
                    row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = true;
                }
            }
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

3、解析