隐式渲染 收集 SphereTracing

Implicit#

何为隐式？隐式（Implicit）的是显式（explicit）的反义词。

explicit可以简单理解为用网格等信息描述的几何形状，网格信息是离散的，信息量越大描述越精准。Implicit则不需要顶点等显式信息，用方程，或者说有符号距离场 (Signed Distance Field) 即SDF，表示几何形状的数学模型。

SDF#

在SDF中，空间中的每一点都有一个值，表示该点到最近表面的距离。这个距离可以是正的（如果点在形状的外部），也可以是负的（如果点在形状的内部）。SDF提供了一种简洁而强大的方式来描述复杂的三维形状，包括难以用传统多边形网格表示的形状。

SDF的优势：

1. 高效的几何操作：进行布尔运算以及形状变形和平滑处理变得简单高效。
2. 复杂形状的表示：特别适合描述复杂或有机形状，如流体、云雾和生物组织。
3. 动态变化的支持：使实时更新和变形成为可能。

对几何primitive的sdf描述
Inigo Quilez :: computer graphics, mathematics, shaders, fractals, demoscene and more (iquilezles.org)

Sphere Tracing#

why#

传统的光线追踪算法，通过发送光线并检测这些光线与场景中物体的交点，进行着色。但是当场景使用SDF来表示时，传统的交点检测方法不再适用。原因在于SDF和多边形网格表示场景的方式截然不同：

1. 顶点表示：在传统的多边形网格表示中，物体由许多小的平面片（通常是三角形）构成的。这些三角形有明确的边界和顶点，因此当光线与这些三角形相交时，可以通过数学计算找到精确的交点。
2. SDF表示：相比之下，SDF场景被视为一个连续的体。体中每个点都有一个值，表示该点到最近表面的距离。这种表示方法不涉及明确的边界或顶点，而是提供关于形状表面的连续信息。

由于SDF没有离散的多边形或边界，传统的光线与多边形的交点检测算法（通常涉及线性代数和平面几何计算）不再适用。在SDF表示的场景中，没有明确的多边形表面可以直接与光线进行交点计算。因此需要Sphere Tracing这样的算法来处理SDF场景。

How#

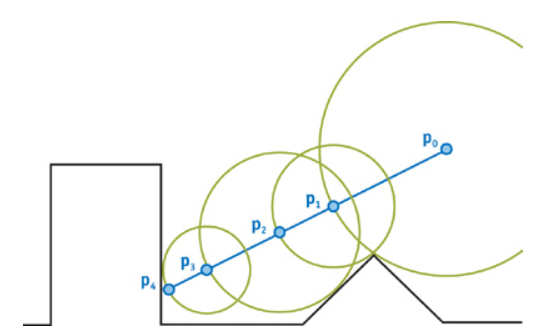
原版的SphereTracing十分讨巧，其基本原理非常简洁，也非常聪明：

1. 从点 $p_0$ 开始投射一条 ray，以 SDF 值 $f\left(p_0\right)$ 为步长进行一次 marching。
2. 以上次 marching 的终点为起点，以 $f\left(p_1\right)$ 为步长继续下一次 marching。
3. 重复 marching 直到 $f\left(p_n\right)$ < $ϵ$ , $ϵ$ 为预设的阈值。此时我们认为 $f\left(p_n\right)$ 即为交点。
   

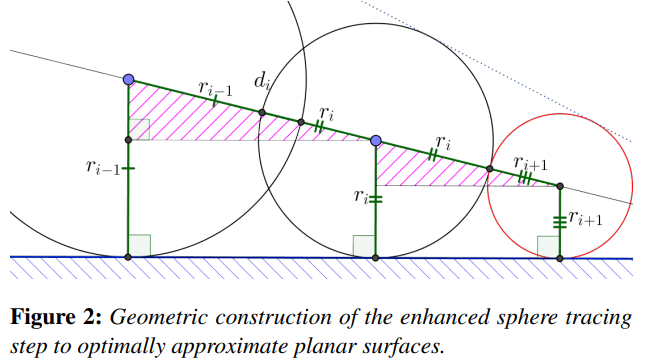
Enhanced Sphere Tracing#

上述的传统 Sphere Tracing 算法冗余的步进次数很多，为了进一步提高效率，诞生了很多种优化方案。

binary search 二分查找法，实际效果不理想，并且遇上TPMS这种复杂结构会有更多问题
Inigo Quilez :: computer graphics, mathematics, shaders, fractals, demoscene and more (iquilezles.org)

Segment Tracing 通过假设场景是 $C^2$ 连续去加长初始 marching 的距离，有效减少 marching 次数的同时，大幅提升了每次 marching 的消耗，效果不理想，并且在有棱角的场景表现更差
https://diglib.eg.org/bitstream/handle/10.1111/cgf13951/v39i2pp545-554.pdf
GitHub - aparis69/Segment-Tracing: Source code for the Computer Graphics Forum paper: Segment Tracing Using Local Lipschitz Bounds. Presented at Eurographics 2020.
【光线追踪】Segment Tracing:一种可能加速距离场求交的实时光线追踪方案 - 知乎 (zhihu.com)
Enhanced Sphere Tracing 采用激进的 marching 步长，即设定一个步长倍数$\alpha$ ，marching 步长改为 $f\left(p_n\right)\ast \alpha$ 而不是 Sphere Tracing 保守的 $f\left(p_n\right)$ 。只要两个 sphere 相交，就说明本次 marching 可安全，否则退回到点 $p_n$ 的位置重新进行保守的 marching。

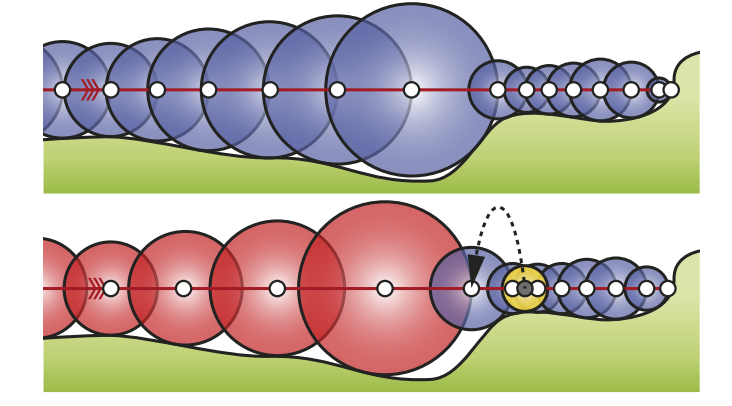
Accelerating Sphere Tracing 在 enhanced 的基础上更进一步。假设前两次 marching 所形成的 sphere 都相切于同一平面，那么下一次可以尝试 marching 同样与该平面相切并且也与上一次的 marching sphere 相切的距离。同样，如果尝试失败则回退至保守 marching。

上述两个方法都是在2023年以前最优秀的 marching 算法之一，直到 Automatic Step Size Relaxation。

Automatic step size relaxation#

Automatic step size relaxation 可以根据历史 marching 的情况，动态调整步长：平面多的地方。可以走相切平面的激进步长，而曲面多的地方则调整为走更保守的步长。

每次 marching 不断更新近似斜率 m，然后用它来指导下一次 marching。

博主拙劣的C++实现

Copy
auto trace_auto_relaxation = [&](glm::vec3 p)
{
	float t = 0.0f;
	float r = sdf(p);
	float m = -1.0f;
	float z = r;
	const float beta = 0.3f;

	for (int i = 0; i < max_steps; i++)
	{
		if (r < eps) {
			return true;
		}
		if (t + r > max_dist) {
			break;
		}

		glm::vec3 next_p = p + ray_dir * z * relaxation_factor;
		float R = sdf(next_p);
		bool doBackStep = z > abs(R) + r;

		if (!doBackStep) {
			float M = (R - r) / (z + 1e-5f);
			m = (1.0f - beta) * m + beta * M;
			t += z * relaxation_factor;
			p = next_p;
			r = R;
		}
		else {
			m = -1.0f;
		}

		float omega = glm::max(1.0f, 2.0f / (1.0f - m));
		z = glm::max(eps, r * omega);
	}
	return false;
};

But#

讲完了吗？讲完我要开始转了。
上述的所有方法，对 TPMS（Triply Periodic Minimal Surfaces 三周期极小曲面），都起不到多少作用。目前效果最好的办法只能是力大砖飞——marching 步长乘以系数 $\alpha ,\alpha <1$ ，以非常保守的步长去小心翼翼的找TPMS表面。也是博主目前最头疼的问题，欢迎讨论。