[数据结构] 串与KMP算法详解

合集 - 数据结构与算法(11)

1.算法3：质数的个数2023-05-012.算法2：Hanoi塔2022-11-223.算法1：Fibonacci数列2022-11-214.[数据结构]排序算法的性能比较01-215.[数据结构] 链表02-036.[数据结构] 栈02-067.[数据结构] 数组与特殊矩阵02-068.[数据结构] 队列02-07

9.[数据结构] 串与KMP算法详解02-12

10.[数据结构] 树与二叉树03-0411.[数据结构] 树、森林及二叉树的应用03-05

收起

写在前面

今天是农历大年初三，祝大家新年快乐！

尽管新旧交替只是一个瞬间，在大家互祝新年快乐的瞬间，在时钟倒计时数到零的瞬间，在烟花在黑色幕布绽放的瞬间，在心底默默许下愿望的瞬间……跨入新的一年，并不意味了一切都会朝着更美好，也没有什么会从天而降，我们赋予了它这份意义，让它自然裹挟着新的爱与希望而来。
当我的视线跃过癸卯兔年，一路的海浪翻涌千叠阳关，才发现此间飘零无关风月，只是山海与风又如期周游了人间一趟。
《人民日报》说，人生这条路很长，未来星辰大海般璀璨，不必踌躇于过去的半亩方塘，这些所谓的遗憾，可能是一种成长，那些曾受过的伤，终会化作光照亮前方的路。
总有一天你会明白，真正治愈你的从来都不是时间，而是你心理的那份释怀与格局，只要你的内心不慌乱，连世界都难影响你。

串的定义和实现

串的定义

串（string）是由零个或多个字符组成的有限序列。一般记为：

$$S{=}^{\prime }{a}_1{a}_2\dots a_n^{\prime }(n\ge 0)$$

其中$S$是串名，$a_i$可以是字母，数字或其他字符。

串中任意连续多个的字符组成的子列称为该串的子串，包含子串的串称为主串。某个字符在串中的序号称为该字符在串中的位置。

$e.g.$ 串$A{=}^{\prime }{\text{China Beijing}}^{\prime },B{=}^{\prime }{\text{Beijing}}^{\prime },C{=}^{\prime }{\text{China}}^{\prime }$，则他们的长度分别是13,7,5，B和C是A的子串，B在A的位置是7。

串的存储结构

定长顺序存储表示

在串的定长顺序存储结构中，每个串变量分配一个固定长度的存储区：

#define MaxLen 255
typedef struct {
    char ch[MaxLen]; // 每个分量存储一个字符
    int length; // 串的实际长度
}String;

串长只能小于等于MaxLen，超过预定义长度的串被舍去，称为截断

串长的两种表述方式：

• 用一个额外的变量len来存放串的长度
• 在串值后面加一个不计入长度的结束标记字符"$\text{ 0}$"，此时串长为隐含值

堆分配存储表示

堆分配存储表示以一组地址连续的存储单元存放串值的字符序列，但存储空间是在程序执行过程中动态分配得到

typedef struct {
    char *ch;
    int length;
}String;

串的匹配模式

简单的模式匹配算法

子串的定位操作通常称为串的模式匹配，它求的是子串（模式串）在主串中的位置。

思想：从文本串的第一个字符开始匹配，如果当前字符匹配成功，则继续匹配下一个字符，否则回溯到上一个匹配的位置，重新从下一个位置开始匹配。如果模式串已经遍历完，说明匹配成功，返回匹配的起始位置，否则匹配失败，返回-1。

int simple_match(char *s, char *p) {
    int i = 0, j = 0;
    while(s[i] != '\0' && p[j] != '\0') {
        if(s[i] == p[j])
            i ++, j ++;
        else {
            i = i - j + 1;
            j = 0;
        }
    }
    if(p[j] == '\0')
        return i - j;
    else
        return -1;
}

这是一种暴力匹算法，时间复杂度为$O(mn)$，m和n分别表示主串和模式串的长度。

我们设主串$S{=}^{\prime }ababcabcacba{b}^{\prime }$，模式串$p{=}^{\prime }abca{c}^{\prime }$进行图解，后文图解两串同。

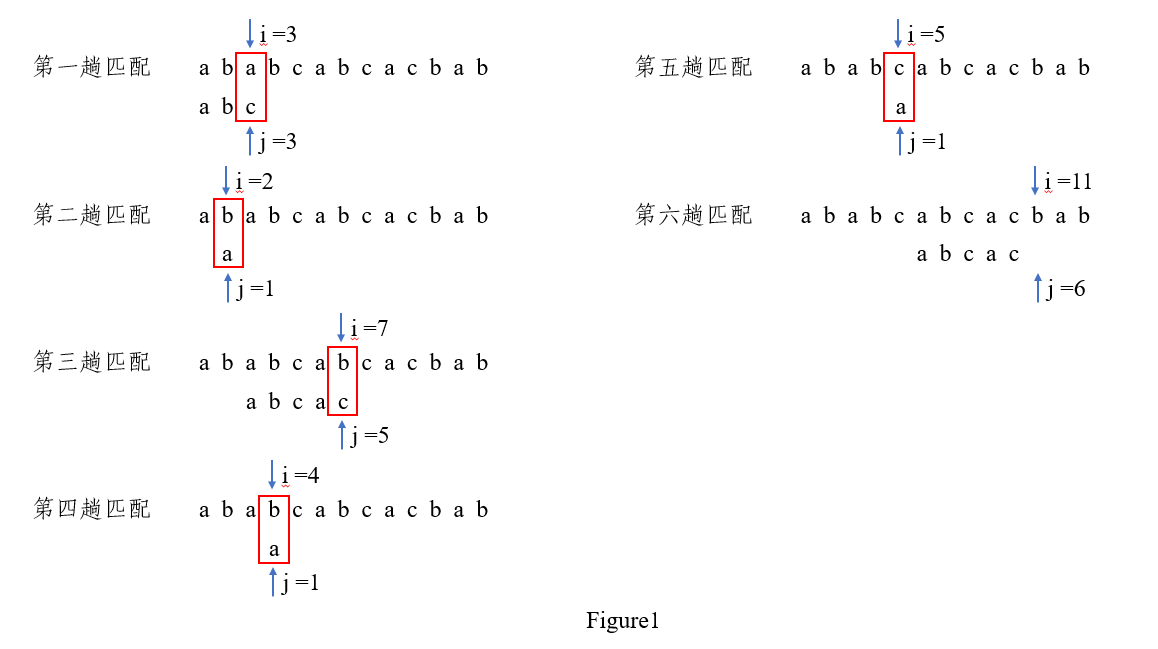
KMP算法

如上图所示，在第三趟匹配中，$i=7,j=5$的字符比较，结果不等，于是回退到$i=4,j=1$重新比较。其实我们可以发现，中间第四、五、六趟比较其实都是不必进行的，可以直接到$i=7,j=2$开始比较。

字符串的前缀、后缀和部分匹配值

前缀：除最后一个字符以外，字符串的所有头部子串；

后缀：除第一个字符外，字符串的所有尾部子串；

部分匹配值：字符串的前缀和后缀的最长相等前后缀长度；

以${}^{\prime }abab{a}^{\prime }$为例：

我们可以得到该字符串的部分匹配值为：00123

回到最初的问题，将模式串改写成数组的形式，得到部分匹配值表（PM表）

编号	1	2	3	4	5
S	a	b	c	a	c
PM	0	0	0	1	0

记住一个公式，非常重要：

$$\mathrm{移}\mathrm{动}\mathrm{位}\mathrm{数}=\mathrm{已}\mathrm{匹}\mathrm{配}\mathrm{的}\mathrm{字}\mathrm{符}\mathrm{数}-\mathrm{对}\mathrm{应}\mathrm{的}\mathrm{部}\mathrm{分}\mathrm{匹}\mathrm{配}\mathrm{值}$$

下面用PM表来进行字符串匹配：

第一趟匹配过程：发现c与a不匹配，前面两个字符ab匹配，查表，最后一个匹配字符b对应的部分匹配值是0，由公式可得，将子串向后移动2位，进行第二趟匹配：

第二趟匹配过程：发现c与b不匹配，前面四个字符abca匹配，最后一个匹配字符a对应的部分匹配值为1，由公式可得，将子串向后移动3位，进行第三趟匹配：

第三趟匹配过程：匹配成功。

整个匹配过程中，主串没有发生过回退，所以KMP算法可以在$O(m+n)$的时间数量级上完成串的模式匹配。

KMP算法的原理

如图2所示，当c与b不匹配时，已匹配的${}^{\prime }abc{a}^{\prime }$的前缀a和后缀a为最长公共元素，因此无需比较，直接将子串按照公式移动对应位数，如图3所示：

对算法的改进方法：

已知：右移位数 = 已匹配的字符数 - 对应的部分匹配值；

写成：$Move=(j-1)-PM[j-1]$。

使用部分匹配值时，每当匹配失败，就去找它前一个元素的部分匹配值，将PM表右移一位，方便直接看自己的部分匹配值。

将例子中模式串PM表右移一位，得到next数组：

编号	1	2	3	4	5
S	a	b	c	a	c
PM	0	0	0	1	0
next	-1	0	0	0	1

• 第一个元素右移以后空缺的用-1来填充，因为若第一个元素匹配失败，则需要将子串右移一位，而不需要计算子串移动的位数；
• 最后一个元素在右移时溢出，因为原来的子串中最后一个元素的部分匹配值是下一个元素使用的，但已经没有下一个元素了，舍去。

于是上式改写成：$Move=(j-1)-next[j]$

最终得到子串指针变化公式 $j=next[j]$。在实际匹配过程中，子串在内存中是不会移动的，而是指针的变化。

$next[j]$的含义是：当子串的第i个字符与主串发生失配时，跳到子串的next[j]位置重新与主串当前位置进行比较。

注

本人在网上查阅相关资料时，没有找到任何有关next数组的推导公式证明，此外由于本人近日感冒腰扭了，坐着打字痛的一批，后面我好了看到这里再补充，接下来我们直接看求next值的代码：

void get_next(char *p, int *next) {
    int i = 0, j = -1;
    next[0] = -1;
    while(p[i] != '\0') {
        if(j == 1 | p[i] == p[j]) {
            i ++, j ++;
            next[i] = j;
        }
        else {
            j = next[j];
        }
    }
}

KMP的代码：

int index_KMP(char *s, char *p, int *next) {
    int i = 0, j = 0;
    int s_len = strlen(s), p_len = strlen(p);
    while(i < s_len && j < p_len) P
        if(j == -1 || s[i] == p[j])
            i ++, j ++;
    	else
            j = next[j];
    if(p[j] == '\0')
        return i - j;
    else
        return -1;
}

题目：来自AcWing 831

给定一个字符串 S，以及一个模式串 P，所有字符串中只包含大小写英文字母以及阿拉伯数字。
模式串 P 在字符串 S 中多次作为子串出现。
求出模式串 P 在字符串 S 中所有出现的位置的起始下标。

输入格式
第一行输入整数 N，表示字符串 P 的长度。
第二行输入字符串 P。
第三行输入整数 M，表示字符串 S 的长度。
第四行输入字符串 S。

输出格式
共一行，输出所有出现位置的起始下标（下标从 0 开始计数），整数之间用空格隔开。

数据范围

$1\le N\le {10}^5$

$1\le M\le {10}^6$

输入样例

3

abc

5

ababa

输出样例

0 2

完整代码

#include
using namespace std;
 
const int N = 100000 + 10, M = 1000000 + 10;
int n, m;
char p[N], s[M];
int next[N];
 
int main() {
    cin >> n >> p + 1 >> m >> s + 1;
    for(int i = 2, j = 0; i <= n; i ++) {
        while(j && p[i] != p[j + 1])
            j = next[j];
        if(p[i] == p[j + 1])
            j ++;
        ne[i] = j;
    }
    for(int i = 1, j = 0; i <= m; i ++) {
        while(j && s[i] != p[j + 1])
            j = next[j];
        if(s[i] == p[j + 1])
            j ++;
        if(j == n) {
            printf("%d ", i - n);
            j = next[j];
        }
    }
    return 0;
}

KMP的进一步优化

这里也仅给出代码，后面再补吧，菜鸡博主痛得不行了

void get_nextval(char *p, int *nextval) {
    int i = 0, j = -1;
    nextval[0] = -1;
    while(p[i] != '\0') {
        if(j == -1 || p[i] == p[j]) {
            i ++, j ++;
            if(p[i] != p[j])
                nextval[j] = j;
            else
                nextval[i] = nextval[j];
        }
        else
            j = nextval[j];
    }
}