代码
原文地址
摘要
文档级关系抽取(DocRE)旨在从文档中抽取出所有实体对的关系。DocRE 面临的一个主要难题是实体对关系之间的复杂依赖性。与大部分隐式地学习强大表示的现有方法不同,最新的 LogiRE 通过学习逻辑规则来显式地建模这种依赖性。但是,LogiRE 需要在训练好骨干网络之后,再用额外的参数化模块进行推理,这种分开的优化过程可能导致结果不够理想。本文提出了 MILR,一个利用挖掘和注入逻辑规则来提升 DocRE 的逻辑框架。MILR 首先基于频率从标注中挖掘出逻辑规则。然后在训练过程中,使用一致性正则化作为辅助损失函数,来惩罚那些违反挖掘规则的样本。最后,MILR 基于整数规划从全局视角进行推理。与 LogiRE 相比,MILR 没有引入任何额外的参数,并且在训练和推理过程中都使用了逻辑规则。在两个基准数据集上的大量实验表明,MILR 不仅提升了关系抽取的性能(1.1%-3.8% F1),而且使预测更加符合逻辑(超过 4.5% Logic)。更重要的是,MILR 在这两个方面都显著优于 LogiRE。
1 Introduction

文档级关系抽取(DocRE):旨在从文档中识别出所有实体对之间的关系。
DocRE 面临的一个主要挑战:实体对之间的关系并非是独立的,而是存在着复杂的依赖关系。例如,在图 1 中,文本只直接表达了 Alisher 是 Chusovitina 的孩子,以及 Bakhodir 和 Chusovitina 是夫妻。但是,根据关系之间的常见依赖关系,可以用图 1 中的逻辑规则来表示,这两个事实就能推导出许多隐含的事实(比如,Alisher 是 Bakhodir 的孩子)。
为了捕获实体对之间的依赖关系,大部分之前的工作都侧重于利用精细的神经网络,如预训练语言模型或图神经网络来学习强大的表示。尽管这些模型取得了很大的成功,但它们缺乏透明性,而且在需要逻辑推理的情况下仍然容易出错。比如,图 1 还展示了一个最先进的 DocRE 模型 ATLOP 的预测结果。可以看到,ATLOP 只提取了一些显式的事实,如 spouse_of(Chusovitina, Bakhodir),而没有识别出一些隐含的事实,如 parent_of(Bakhodir, Alisher)。实际上,这些隐含的事实可以通过显式地考虑关系之间的逻辑规则来更容易地识别(比如,parent_of(v0, v2) ← spouse_of(v0, v1) ∧ parent_of(v1, v2))。基于此,LogiRE提出了一种方法,它基于训练好的 DocRE 模型(即骨干网络)的输出对数来生成逻辑规则,并通过对规则进行推理来重新提取关系。然而,LogiRE 需要在训练好骨干网络之后,再使用额外的参数化模块来进行推理,这种分离的优化过程可能导致结果不够理想。比如,LogiRE 不能在训练过程中让骨干网络具有逻辑一致性的感知,而且可能导致错误的累积。
为了提升DocRE的效果,本文提出了一个通用的框架 MILR,它能够挖掘和注入逻辑规则。由于现有的逻辑规则不够明确,MILR 首先根据训练集上的条件相对频率来发现逻辑规则。然后,它利用一致性正则化作为一个辅助损失函数,对违反发现规则的训练实例进行惩罚。一致性正则化和常见的分类损失函数相结合,用于训练骨干网络。最后,MILR 采用了一种基于 0-1 整数规划的全局推理方法,它可以视为在逻辑约束条件下对基于阈值的推理方法的一种扩展。这样,MILR 能够使骨干网络在训练和预测时将所有关系作为一个整体来处理,显式地捕捉关系之间的依赖性,从而增强解释性。
2 Preliminaries
Problem Formulation
DocRE的目的是从完整的文档中找出多个实体之间的语义关系。给定一个文档 ,其中包含
,其中包含 个命名实体
个命名实体 ,DocRE 需要预测每一对不同的实体
,DocRE 需要预测每一对不同的实体 之间的关系类型。关系类型的集合是
之间的关系类型。关系类型的集合是 ,其中
,其中 是预先定义好的,
是预先定义好的, 表示“无关系”。DocRE比句子级关系抽取更具挑战性,因为它需要综合利用文档中多个句子的信息,并处理跨句实体之间的复杂依赖关系。
表示“无关系”。DocRE比句子级关系抽取更具挑战性,因为它需要综合利用文档中多个句子的信息,并处理跨句实体之间的复杂依赖关系。
 ,其中包含
,其中包含 个命名实体
个命名实体 ,DocRE 需要预测每一对不同的实体
,DocRE 需要预测每一对不同的实体 之间的关系类型。关系类型的集合是
之间的关系类型。关系类型的集合是 ,其中
,其中 是预先定义好的,
是预先定义好的, 表示“无关系”。DocRE比句子级关系抽取更具挑战性,因为它需要综合利用文档中多个句子的信息,并处理跨句实体之间的复杂依赖关系。
表示“无关系”。DocRE比句子级关系抽取更具挑战性,因为它需要综合利用文档中多个句子的信息,并处理跨句实体之间的复杂依赖关系。Atoms and Rules
一个原子 (或
(或 ) 是一个二元变量,表示头实体
) 是一个二元变量,表示头实体 和尾实体
和尾实体 之间是否存在关系
之间是否存在关系  。如果存在,
。如果存在, 。否则
。否则  。
。
 (或
(或 ) 是一个二元变量,表示头实体
) 是一个二元变量,表示头实体 和尾实体
和尾实体 之间是否存在关系
之间是否存在关系  。如果存在,
。如果存在, 。否则
。否则  。
。规则是一个具有如下形式的合取公式:

其中
 是表示任意实体的变量,
是表示任意实体的变量, 是规则的长度。
是规则的长度。 和
和 分别称为头原子和体原子。本文采用概率软逻辑 (Kimmig 等人, 2012; Bach 等人, 2017) 的框架,给每个规则赋予一个置信度属性,其值在 [0, 1] 区间内。一个规则
分别称为头原子和体原子。本文采用概率软逻辑 (Kimmig 等人, 2012; Bach 等人, 2017) 的框架,给每个规则赋予一个置信度属性,其值在 [0, 1] 区间内。一个规则  可以被看作是一个模板,它可以通过将
可以被看作是一个模板,它可以通过将  从变量替换为特定的实体
从变量替换为特定的实体  来实例化(记为
来实例化(记为  )。如果
)。如果 的所有体原子都成立,称
的所有体原子都成立,称  是一个由
是一个由  推导出的预测,即预测头原子由于
推导出的预测,即预测头原子由于  而成立。注意,一个不合理的规则可能没有对应的预测,因为它的体原子不可能同时成立。
而成立。注意,一个不合理的规则可能没有对应的预测,因为它的体原子不可能同时成立。

 是表示任意实体的变量,
是表示任意实体的变量, 是规则的长度。
是规则的长度。 和
和 分别称为头原子和体原子。本文采用概率软逻辑 (Kimmig 等人, 2012; Bach 等人, 2017) 的框架,给每个规则赋予一个置信度属性,其值在 [0, 1] 区间内。一个规则
分别称为头原子和体原子。本文采用概率软逻辑 (Kimmig 等人, 2012; Bach 等人, 2017) 的框架,给每个规则赋予一个置信度属性,其值在 [0, 1] 区间内。一个规则  可以被看作是一个模板,它可以通过将
可以被看作是一个模板,它可以通过将  从变量替换为特定的实体
从变量替换为特定的实体  来实例化(记为
来实例化(记为  )。如果
)。如果 的所有体原子都成立,称
的所有体原子都成立,称  是一个由
是一个由  推导出的预测,即预测头原子由于
推导出的预测,即预测头原子由于  而成立。注意,一个不合理的规则可能没有对应的预测,因为它的体原子不可能同时成立。
而成立。注意,一个不合理的规则可能没有对应的预测,因为它的体原子不可能同时成立。Paradigm of Backbones
对于每个原子 ,
, 表示其对数几率。通过sigmoid函数,
表示其对数几率。通过sigmoid函数, 可以用来估计在给定
可以用来估计在给定 的条件下,关系
的条件下,关系 是否成立的概率,即
是否成立的概率,即
 ,
, 表示其对数几率。通过sigmoid函数,
表示其对数几率。通过sigmoid函数, 可以用来估计在给定
可以用来估计在给定 的条件下,关系
的条件下,关系 是否成立的概率,即
是否成立的概率,即
其中 是sigmoid函数。
是sigmoid函数。
 是sigmoid函数。
是sigmoid函数。为了训练模型,使用分类损失函数(例如,二元交叉熵(BCE)损失或自适应阈值损失来优化目标函数(即 )。
)。
 )。
)。在推理过程中,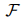 通过将预测概率与分类阈值进行比较来确定
通过将预测概率与分类阈值进行比较来确定 的预测关系:
的预测关系:
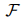 通过将预测概率与分类阈值进行比较来确定
通过将预测概率与分类阈值进行比较来确定 的预测关系:
的预测关系:
其中 表示
表示 是一个预测事实,反之则否,
是一个预测事实,反之则否, 表示指示函数,
表示指示函数, 是
是 的分类阈值。常见的基于阈值的推理方法有全局阈值法(Yao等,2019;Zeng等,2020)和自适应阈值法(Zhou等,2021a;Yang Zhou等,2022)。这两种方法的主要区别在于
的分类阈值。常见的基于阈值的推理方法有全局阈值法(Yao等,2019;Zeng等,2020)和自适应阈值法(Zhou等,2021a;Yang Zhou等,2022)。这两种方法的主要区别在于 是否与
是否与 相关。
相关。
 表示
表示 是一个预测事实,反之则否,
是一个预测事实,反之则否, 表示指示函数,
表示指示函数, 是
是 的分类阈值。常见的基于阈值的推理方法有全局阈值法(Yao等,2019;Zeng等,2020)和自适应阈值法(Zhou等,2021a;Yang Zhou等,2022)。这两种方法的主要区别在于
的分类阈值。常见的基于阈值的推理方法有全局阈值法(Yao等,2019;Zeng等,2020)和自适应阈值法(Zhou等,2021a;Yang Zhou等,2022)。这两种方法的主要区别在于 是否与
是否与 相关。
相关。3 Methodology

本文提出了一种与模型无关的框架 MILR,它能够让现有的 DocRE 模型在训练和推理时具有逻辑一致性。MILR 的核心思想是,既要约束输出的对数几率,也要约束最终的预测,使它们符合逻辑规则。由于大多数数据集没有提供金标准的逻辑规则,MILR 采用了一种从关系标注中直接挖掘规则的数据驱动方法(见第 3.1 节)。在训练时,MILR 通过一致性正则化作为一个辅助损失,来惩罚那些违反挖掘规则的实例(见第 3.2 节)。在推理时,MILR 将对数几率和挖掘规则结合起来,进行全局预测(见第 3.3 节)。最后,第 3.4 节对 MILR 和 LogiRE 进行了详细的比较。
3.1 Rule Mining

受知识库和知识图谱相关工作的启发,MILR 采用了一种基于频率的简单而有效的方法来挖掘逻辑规则。直观地说,如果一个规则能够反映关系之间的依赖性,例如 child_of(v0, v1) ← parent_of(v1, v0),那么它的头原子就倾向于与它的体原子同时出现。此外,一个规则的置信度可以通过当体原子成立时,头原子成立的条件概率来估计。
本文采用了闭世界假设(CWA),即认为任何不在关系标注中的原子都是反例。在 CWA 下,如果一个规则  的预测
的预测  的头原子在标注中,就称
的头原子在标注中,就称  为真预测。否则,称之为假预测。一个规则
为真预测。否则,称之为假预测。一个规则  的置信度定义为所有预测中真预测的比例:
的置信度定义为所有预测中真预测的比例:
 的预测
的预测  的头原子在标注中,就称
的头原子在标注中,就称  为真预测。否则,称之为假预测。一个规则
为真预测。否则,称之为假预测。一个规则  的置信度定义为所有预测中真预测的比例:
的置信度定义为所有预测中真预测的比例:
其中 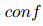 是
是  的缩写,
的缩写, 和
和 分别是规则
分别是规则  在训练集中的真预测和假预测的数量。公式 4 可以看作是用条件相对频率来估计条件概率。注意,如果一个规则
在训练集中的真预测和假预测的数量。公式 4 可以看作是用条件相对频率来估计条件概率。注意,如果一个规则  没有预测,
没有预测,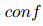 被设为 0。
被设为 0。
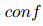 是
是  的缩写,
的缩写, 和
和 分别是规则
分别是规则  在训练集中的真预测和假预测的数量。公式 4 可以看作是用条件相对频率来估计条件概率。注意,如果一个规则
在训练集中的真预测和假预测的数量。公式 4 可以看作是用条件相对频率来估计条件概率。注意,如果一个规则  没有预测,
没有预测,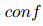 被设为 0。
被设为 0。规则挖掘器(RM)以训练集的标注  、扩展的关系集
、扩展的关系集  、构造规则的最大长度
、构造规则的最大长度 和过滤荒谬规则的最小置信度
和过滤荒谬规则的最小置信度  作为输入。如算法 1 所示,RM 枚举所有可能的规则(第 2-4 行)。在枚举过程中,RM 根据公式 4 计算
作为输入。如算法 1 所示,RM 枚举所有可能的规则(第 2-4 行)。在枚举过程中,RM 根据公式 4 计算 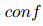 (第 5 行)。如果
(第 5 行)。如果 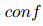 高于
高于  ,RM 将
,RM 将  和相应的
和相应的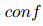 添加到输出中(第 6-7 行)。
添加到输出中(第 6-7 行)。
 、扩展的关系集
、扩展的关系集  、构造规则的最大长度
、构造规则的最大长度 和过滤荒谬规则的最小置信度
和过滤荒谬规则的最小置信度  作为输入。如算法 1 所示,RM 枚举所有可能的规则(第 2-4 行)。在枚举过程中,RM 根据公式 4 计算
作为输入。如算法 1 所示,RM 枚举所有可能的规则(第 2-4 行)。在枚举过程中,RM 根据公式 4 计算 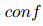 (第 5 行)。如果
(第 5 行)。如果 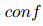 高于
高于  ,RM 将
,RM 将  和相应的
和相应的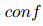 添加到输出中(第 6-7 行)。
添加到输出中(第 6-7 行)。3.2 Consistency Regularization
为了统一离散的约束和现有的 DocRE 模型的损失驱动的学习范式,本文需要解决一个关键的技术问题:如何在具有置信度的逻辑规则下进行推理。本文借鉴了乘积 t-范数的思想,将一个规则 R 的理想概率形式定义为

其中  是
是  的长度,
的长度, 是一个与
是一个与  相关的松弛超参数,
相关的松弛超参数, 是由公式 2 计算的输出概率。在这个定义下,如果一个规则的置信度很高(接近 1),那么它的头原子的概率应该不低于它的体原子的联合概率,这里简单地用
是由公式 2 计算的输出概率。在这个定义下,如果一个规则的置信度很高(接近 1),那么它的头原子的概率应该不低于它的体原子的联合概率,这里简单地用  来近似。这意味着规则的头原子可以由它的体原子或其他途径推出,比如明确的上下文或其他有相同头原子的规则。随着置信度的降低,这个约束也会相应地放宽。(本文定义
来近似。这意味着规则的头原子可以由它的体原子或其他途径推出,比如明确的上下文或其他有相同头原子的规则。随着置信度的降低,这个约束也会相应地放宽。(本文定义 )
)
 是
是  的长度,
的长度, 是一个与
是一个与  相关的松弛超参数,
相关的松弛超参数, 是由公式 2 计算的输出概率。在这个定义下,如果一个规则的置信度很高(接近 1),那么它的头原子的概率应该不低于它的体原子的联合概率,这里简单地用
是由公式 2 计算的输出概率。在这个定义下,如果一个规则的置信度很高(接近 1),那么它的头原子的概率应该不低于它的体原子的联合概率,这里简单地用  来近似。这意味着规则的头原子可以由它的体原子或其他途径推出,比如明确的上下文或其他有相同头原子的规则。随着置信度的降低,这个约束也会相应地放宽。(本文定义
来近似。这意味着规则的头原子可以由它的体原子或其他途径推出,比如明确的上下文或其他有相同头原子的规则。随着置信度的降低,这个约束也会相应地放宽。(本文定义 )
)然而,如果没有正则化,上述规则的理想概率形式在训练骨干网络时很可能被破坏,特别是当头原子的关系类型是不常见的时候(Huang 等人, 2022)。因此,本文认为,除了 DocRE 模型的原始分类损失 外,还有另一个与逻辑一致性相关的损失
外,还有另一个与逻辑一致性相关的损失  ,应该被最小化。为了将
,应该被最小化。为了将  和
和  都放在概率的对数空间中,给定一个文档
都放在概率的对数空间中,给定一个文档  ,将
,将  表示为
表示为
 外,还有另一个与逻辑一致性相关的损失
外,还有另一个与逻辑一致性相关的损失  ,应该被最小化。为了将
,应该被最小化。为了将  和
和  都放在概率的对数空间中,给定一个文档
都放在概率的对数空间中,给定一个文档  ,将
,将  表示为
表示为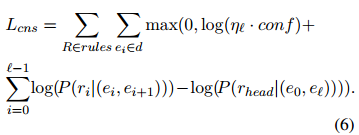
 枚举了所有实例化的规则,并正则化相应的对数值,使其满足公式 5 定义的理想形式。如果规则的理想概率形式几乎被满足,那么一致性正则化损失
枚举了所有实例化的规则,并正则化相应的对数值,使其满足公式 5 定义的理想形式。如果规则的理想概率形式几乎被满足,那么一致性正则化损失  及其梯度都很小,因此对骨干网络的训练影响不大。如果不是,
及其梯度都很小,因此对骨干网络的训练影响不大。如果不是, 将在训练中产生很大的梯度幅度,从而正则化骨干网络以满足逻辑一致性。
将在训练中产生很大的梯度幅度,从而正则化骨干网络以满足逻辑一致性。总之,MILR 中的训练目标是

其中  是一个用于平衡两个损失的超参数。通过这种方式,学习过程试图统一单个原子的似然性质和多个关系之间的逻辑性质,从而支持骨干网络全面理解给定的注释。
是一个用于平衡两个损失的超参数。通过这种方式,学习过程试图统一单个原子的似然性质和多个关系之间的逻辑性质,从而支持骨干网络全面理解给定的注释。
 是一个用于平衡两个损失的超参数。通过这种方式,学习过程试图统一单个原子的似然性质和多个关系之间的逻辑性质,从而支持骨干网络全面理解给定的注释。
是一个用于平衡两个损失的超参数。通过这种方式,学习过程试图统一单个原子的似然性质和多个关系之间的逻辑性质,从而支持骨干网络全面理解给定的注释。3.3 Global Inference
尽管在训练过程中,已经注入了逻辑规则,但骨干网络在推理过程中仍有可能产生违反逻辑规则的预测。为了解决这个问题,MILR 采用了一种基于编程的方法,在推理过程中强制执行逻辑规则,从而实现了一种全局推理方法。这种方法可以看作是公式 3 中提到的基于阈值的方法的一种改进。为了便于理解,先回顾一下基于阈值的方法,并从 0-1 整数规划的角度进行分析:
Fact 1.
设  为一个 DocRE 模型,
为一个 DocRE 模型, 为输出的对数值,
为输出的对数值, 为阈值,
为阈值, 为原子
为原子  的预测结果,
的预测结果,
 。对于以下问题:
。对于以下问题:
 为一个 DocRE 模型,
为一个 DocRE 模型, 为输出的对数值,
为输出的对数值, 为阈值,
为阈值, 为原子
为原子  的预测结果,
的预测结果,
 。对于以下问题:
。对于以下问题:
一个最优解是  ,其中
,其中  。证明见附录 A。目标函数的构造受到了 BCE 损失函数的启发。因此,基于阈值的方法可以被看作是利用潜在的预测结果
。证明见附录 A。目标函数的构造受到了 BCE 损失函数的启发。因此,基于阈值的方法可以被看作是利用潜在的预测结果  作为二元决策变量,无约束地最小化分布
作为二元决策变量,无约束地最小化分布  相对于分布
相对于分布  的交叉熵之和。
的交叉熵之和。
 ,其中
,其中  。证明见附录 A。目标函数的构造受到了 BCE 损失函数的启发。因此,基于阈值的方法可以被看作是利用潜在的预测结果
。证明见附录 A。目标函数的构造受到了 BCE 损失函数的启发。因此,基于阈值的方法可以被看作是利用潜在的预测结果  作为二元决策变量,无约束地最小化分布
作为二元决策变量,无约束地最小化分布  相对于分布
相对于分布  的交叉熵之和。
的交叉熵之和。这种观点激发了本文将逻辑规则作为编程问题的约束条件。直观地说,对于一个规则  ,逻辑一致性要求它的预测体原子都成立,那么它的预测头原子也成立。如果任何一个体原子失败,逻辑一致性对预测头原子没有约束。这可以用数学表达为
,逻辑一致性要求它的预测体原子都成立,那么它的预测头原子也成立。如果任何一个体原子失败,逻辑一致性对预测头原子没有约束。这可以用数学表达为 
 。添加这些逻辑约束和对称约束,就可以得到全局推理方法的原始形式:
。添加这些逻辑约束和对称约束,就可以得到全局推理方法的原始形式:
 ,逻辑一致性要求它的预测体原子都成立,那么它的预测头原子也成立。如果任何一个体原子失败,逻辑一致性对预测头原子没有约束。这可以用数学表达为
,逻辑一致性要求它的预测体原子都成立,那么它的预测头原子也成立。如果任何一个体原子失败,逻辑一致性对预测头原子没有约束。这可以用数学表达为 
 。添加这些逻辑约束和对称约束,就可以得到全局推理方法的原始形式:
。添加这些逻辑约束和对称约束,就可以得到全局推理方法的原始形式:
这种原始形式的目标是利用推理结果在逻辑约束下最小化 BCE 损失,与公式 7 定义的训练目标相一致。可以用分支定界法 (Lawler 和 Wood, 1966) 或现成的优化器如 Gurobi (Gurobi Optimization, LLC, 2022) 来求解这种原始形式。
但是,这个问题涉及  个逻辑约束,其中
个逻辑约束,其中  是实体的数量。这些冗余的约束会导致计算速度非常慢。为了解决这个问题,本文提出了一种启发式策略来简化约束,具体见算法 2。该策略的思想是,只对那些由基于阈值的方法预测为真的体原子的预测施加逻辑约束,用逻辑规则来修正它们和相应的头原子。而其他原子的预测结果则保持与通过阈值化概率产生的银标签一致。从数学上看,这种策略相当于对最优解处的正约束做了近似。这样做的好处是,由于大多数实体对没有关系,约束的数量可以大大减少。
是实体的数量。这些冗余的约束会导致计算速度非常慢。为了解决这个问题,本文提出了一种启发式策略来简化约束,具体见算法 2。该策略的思想是,只对那些由基于阈值的方法预测为真的体原子的预测施加逻辑约束,用逻辑规则来修正它们和相应的头原子。而其他原子的预测结果则保持与通过阈值化概率产生的银标签一致。从数学上看,这种策略相当于对最优解处的正约束做了近似。这样做的好处是,由于大多数实体对没有关系,约束的数量可以大大减少。
 个逻辑约束,其中
个逻辑约束,其中  是实体的数量。这些冗余的约束会导致计算速度非常慢。为了解决这个问题,本文提出了一种启发式策略来简化约束,具体见算法 2。该策略的思想是,只对那些由基于阈值的方法预测为真的体原子的预测施加逻辑约束,用逻辑规则来修正它们和相应的头原子。而其他原子的预测结果则保持与通过阈值化概率产生的银标签一致。从数学上看,这种策略相当于对最优解处的正约束做了近似。这样做的好处是,由于大多数实体对没有关系,约束的数量可以大大减少。
是实体的数量。这些冗余的约束会导致计算速度非常慢。为了解决这个问题,本文提出了一种启发式策略来简化约束,具体见算法 2。该策略的思想是,只对那些由基于阈值的方法预测为真的体原子的预测施加逻辑约束,用逻辑规则来修正它们和相应的头原子。而其他原子的预测结果则保持与通过阈值化概率产生的银标签一致。从数学上看,这种策略相当于对最优解处的正约束做了近似。这样做的好处是,由于大多数实体对没有关系,约束的数量可以大大减少。
在评估模型时,本文发现添加补偿项来构造目标函数可以进一步提高性能。修改后的目标函数如下:

其中, 是超参数,
是超参数,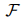 是在训练集上评估的关系
是在训练集上评估的关系 的频率。这些补偿项可以帮助缓解DocRE的类不平衡问题。
的频率。这些补偿项可以帮助缓解DocRE的类不平衡问题。
 是超参数,
是超参数,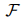 是在训练集上评估的关系
是在训练集上评估的关系 的频率。这些补偿项可以帮助缓解DocRE的类不平衡问题。
的频率。这些补偿项可以帮助缓解DocRE的类不平衡问题。总之,最终的全局推理形式以公式10为目标,并利用算法2构造逻辑约束集合。基于整数规划,可以过滤掉低概率的逻辑不一致,从而提高性能和可解释性。
3.4 Comparison with LogiRE
LogiRE 和 MILR 都是将逻辑规则注入到主干网络的方法,但 MILR 有以下三个优势。首先,MILR 不需要额外训练任何模块,因此更加高效。其次,MILR 在训练过程中利用一致性正则化,使主干网络具有逻辑一致性的能力。而 LogiRE 不改变训练过程,所以主干网络更容易受到噪声标签的影响,这在 DocRE (Huang等人, 2022) 中是比较常见的情况。第三,MILR 可以处理更多种类的错误,这些错误是根据它们发生在逻辑规则的哪个部分来分类的。MILR 在推理过程中采用了一种基于编程的方法,可以在理论上减少头原子的假阴性 (FNH) 和体原子的假阳性 (FPB)。相反,LogiRE 只能处理 FNH,因为 LogiRE 是通过元路径来计算要评估的原子的最终逻辑值的,这些逻辑值可能被主干网络误导。当 LogiRE 遇到 FPB (即主干网络错误地为不成立的三元组输出了高逻辑值) 时,LogiRE 就会盲目地认为这些逻辑值是真阳性,从而导致头原子的假阳性 (FPH)。值得注意的是,MILR 和 LogiRE 都无法处理 FPH 和体原子的假阴性 (FNB),因为这些情况下没有什么可以推理的,逻辑约束已经被满足了。为了方便理解,本文在表1中对上述讨论进行了总结。
