数据结构之队列

 💕"

开朗些，勇敢些

"💕

作者：Mylvzi 

 文章主要内容：数据结构之队列及其面试题 

一.队列

1.概念

  队列：只允许在一端进行数据的插入(队尾),在另一端进行数据的删除(队头)的特殊线性表，和栈不同的是，队列具有先进先出的特性(FIFO)

2.java中的队列

  Java中队列是一个接口，底层是通过链表实现的；既然是接口，就不能直接实例化对象，要利用实现queue接口的类去实例化对象

源码

二.队列的模拟实现

  队列的底层是是LinkdList，所以可以使用双向链表实现队列

    /**
     * 实现队尾进，队头出
     */
 
    public void offer(int x) {
        ListNode node = new ListNode(x);
        if (rear == null) {
            front = rear = node;
            this.usedSize++;
            return;
        }
 
        rear.next = node;
        node.prev = rear;
        rear = node;
 
        this.usedSize++;
    }
 
    public int poll() {
        if (front == null) {
            throw new QueueEmptyException("队列为空，无法返回数据");
        }
 
        int ret = front.val;
 
        // 如果只有一个节点  要把front和rear都置空  否则在执行front.prev = null这句代码时会报错
        if (front.next == null) {
            front = null;
            rear = null;
            return ret;
        }
 
        front = front.next;
        front.prev = null;
 
        this.usedSize--;
        return ret;
    }
 
    public int peek() {
        if (front == null) {
            throw new QueueEmptyException("队列为空，无法返回数据");
        }
 
        int ret = front.val;
        return ret;
    }
 
    public int size() {
        return this.usedSize;
    }
 
    public boolean empty() {
        return this.usedSize==0;
    }
 
}

 3.Deque

  Deque也是Java中和队列有关的数据结构，它是一种双端队列，即队头，队尾都可以实现数据插入与删除，deque 是 “double ended queue” 的简称。同时Deque也是Java中最常用的queue结构  

源码：

4.循环队列的实现

所谓循环队列就是front和rear一直在绕着圆走，和普通队列不一样的是，它可以重复利用空间

循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

一般的队列

循环队列

循环队列的难点在于如何判满，这里我们提供两种方法 

循环队列的实现1:使用计数器

class MyCircularQueue {
    
    private int[] elem;
    private int front;
    private int rear;
    private int cnt = 0;
    
 
    public MyCircularQueue(int k) {
        this.elem = new int[k];
    }
 
    public boolean enQueue(int value) {
        // 插入数据
        if(isFull()) {
            return false;
        }
        
        this.elem[rear] = value;
        rear = (rear+1) % elem.length;
        cnt++;
        return true;
        
    }
 
    public boolean deQueue() {
        if(isEmpty()) {
            return false;
        }
        
        front = (front+1) % elem.length;
        cnt--;
        return true;
 
    }
 
    public int Front() {
        if(isEmpty()) {
            return -1;
        }
        return this.elem[front];
    }
 
    public int Rear() {
               if (isEmpty()) {
            return -1;
        }
        int index = (rear == 0) ? (elem.length-1) : (rear-1);
        return this.elem[index];
    }
 
    public boolean isEmpty() {
        return cnt == 0;
    }
 
    public boolean isFull() {
        return cnt == this.elem.length;
    }
}

 循环队列的实现2:预留一个空间

class MyCircularQueue {
 
    private int[] elem;
    private int front;
    private int rear;
 
    public MyCircularQueue(int k) {
        this.elem = new int[k+1];
    }
 
    public boolean enQueue(int value) {
        // 插入数据
        if(isFull()) {
            return false;
        }
 
        this.elem[rear] = value;
        rear = (rear+1) % elem.length;
        return true;
 
    }
 
    public boolean deQueue() {
        if(isEmpty()) {
            return false;
        }
 
        front = (front+1) % elem.length;
        return true;
 
    }
 
    public int Front() {
        if(isEmpty()) {
            return -1;
        }
        return this.elem[front];
    }
 
    public int Rear() {
                if(isEmpty()) {
            return -1;
        }
        int index = (rear == 0) ? (elem.length-1) : (rear-1);
        return this.elem[index];
    }
 
    public boolean isEmpty() {
        return rear == front;
    }
 
    public boolean isFull() {
        return (rear+1) % elem.length == front;
    }
}

注意：为了实现循环，rear和front的变化不能直接写成rear++或者front++，否则会发生越界

rear = (rear+1) % elem.length;

front = (front+1) % elem.length;

用队列实现栈

225. 用队列实现栈 - 力扣（LeetCode）

1.使用两个队列

  利用两个队列实现栈

如果是入栈，入到不为空的队列之中

如果是出栈，先找到不为空的队列，将队尾之前的所有元素出到另一个队列之中，最后再出队尾元素，实现后进先出

如果是返回栈顶元素，和出栈的思路一样，栈顶就是不为空队列的队尾

栈为空：当两个队列都为空时，栈为空

/**
 * 用队列实现栈  使用两个队列实现栈
 * 队列:先进先出  栈:后进先出
 * 要明白,一个队列无法实现栈,他们有本质上的区别
 * 入栈:入到不为空的队列之中  如果两个都为空,入到第一个队列之中
 * 出栈:出栈顶元素,后进先出  对应的是队列中的队尾元素  将队尾元素之前的所有元素转移到另一个队列之中,再返回队尾元素
 */
class MyStack2 {
    private Queue que1;
    private Queue que2;
 
 
    public MyStack2() {
        this.que1 = new LinkedList<>();
        this.que2 = new LinkedList<>();
    }
 
    public void push(int x) {
        // 入栈到不为空的队列之中
        if(!que1.isEmpty()) {
            que1.offer(x);
        } else if (!que2.isEmpty()) {
            que2.offer(x);
        }else {
            que1.offer(x);
        }
 
 
    }
 
    public int pop() {
        // 出栈
        // 为空  直接返回
        if (empty()) {
            return -1;
        }
 
 
        if (!que1.isEmpty()) {
            int size = que1.size();
            for (int i = 0; i < size - 1; i++) {
                // 将que1队尾元素前面的所有元素转移到que2中
                que2.offer(que1.poll());
            }
            return que1.poll();
        } else {
            int size = que2.size();
            for (int i = 0; i < size - 1; i++) {
                // 将que2队尾元素前面的所有元素转移到que1中
                que1.offer(que2.poll());
            }
            return que2.poll();
        }
 
    }
 
    public int top() {
        // 为空  直接返回
        if (empty()) {
            return -1;
        }
 
        int tmp = -1;
 
        if (!que1.isEmpty()) {
            int size = que1.size();
            for (int i = 0; i < size; i++) {
                // 将que1队尾元素前面的所有元素转移到que2中
                tmp = que1.poll();
                que2.offer(tmp);
            }
            return tmp;
        } else {
            int size = que2.size();
            for (int i = 0; i < size - 1; i++) {
                // 将que2队尾元素前面的所有元素转移到que1中
                tmp = que2.poll();
                que1.offer(tmp);
            }
            return tmp;
        }
 
    }
 
    public boolean empty() {
        // 当两个队列都为空时,栈就为空
        return que1.isEmpty() && que2.isEmpty();
    }
}

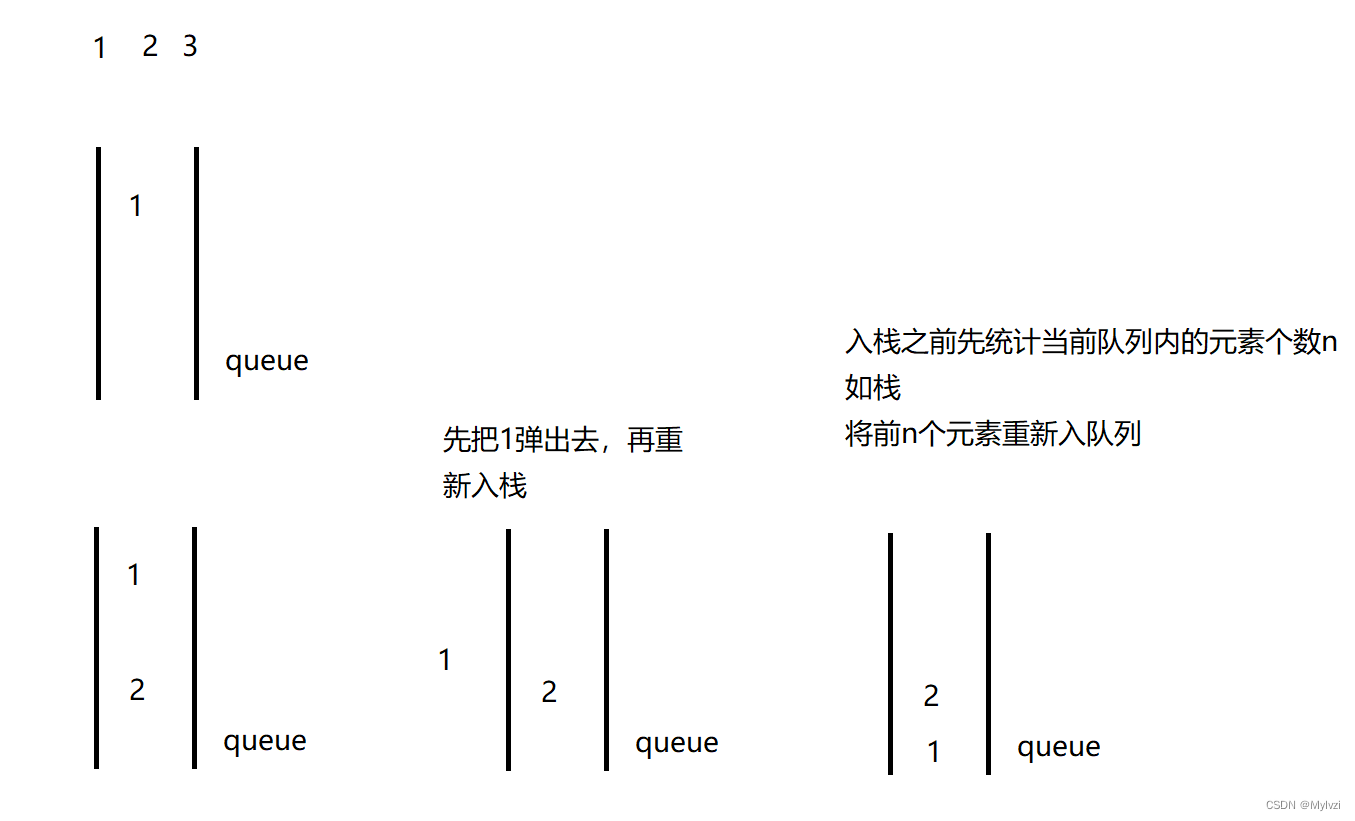
 2.使用一个队列

/**
 * 思路2:使用一个队列实现栈
 * 栈:后进先出   队列:先进后出
 * 保证队头的元素时最后一个入栈的
 * 新入一个元素的时候将之前所有元素都poll出去,再重新入队,那么新元素就是队头了
 * 这样就实现了后进先出
 */
class MyStack2 {
 
    Queue queue;
 
    public MyStack2() {
        this.queue = new LinkedList<>();
    }
 
 
    public void push(int x) {
        int n = queue.size();
        queue.offer(x);
 
        for (int i = 0; i < n; i++) {
            // 重新入队
            queue.offer(queue.poll());
//            int ret = queue.poll();
//            queue.offer(ret);
        }
 
    }
 
    public int pop() {
        return queue.poll();
    }
 
    public int top() {
        return queue.peek();
    }
 
    public boolean empty() {
        return queue.isEmpty();
    }
}

可以带入数据尝试一下  之所以需要%N,是因为rear有可能处于下标为0的位置