二分查找——经典题目合集

文章目录

• • 🦜69. x 的平方根
  • • 🌼题目
    • 🌻算法原理
    • 🌷代码实现
  • 🐳35. 搜索插入位置
  • • 🌼题目
    • 🌻算法原理
    • 🌷代码实现
  • 🦭852. 山脉数组的峰顶索引
  • • 🌼题目
    • 🌻算法原理
    • 代码实现
  • 🐧162. 寻找峰值
  • • 🌼题目
    • 🌻算法原理
    • 🌷代码实现
  • 🦚153. 寻找旋转排序数组中的最小值
  • • 🌼题目
    • 🌻算法原理
    • 🌷代码实现
  • 🦖LCR 173. 点名
  • • 🌼题目
    • 🌻算法原理
    • 🌷代码实现

704.二分查找、34. 在排序数组中查找元素的第一个和最后一个位置（二分查找模板）

🦜69. x 的平方根

🌼题目

题目链接：69. x 的平方根 - 力扣（LeetCode）

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意： 不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

输入：x = 4
输出：2
1
2

示例 2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。
1
2
3

提示：

• 0 <= x <= 231 - 1

🌻算法原理

本题采用二分查找，题目给的x，要求是有符合的平方根就返回该x的平方根，如果没有则返回小于它的整数平方根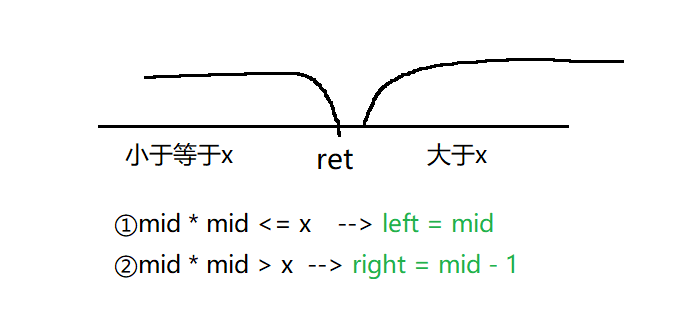

🌷代码实现

class Solution {
public:
    int mySqrt(int x) {
        if(x<1) return 0;	//处理边界
        int left = 1;
        int right = x;
        while(left<right)
        {
            long long mid = left+(right-left+1)/2;	//long long防止溢出
            if(mid*mid <= x)    left = mid;
            else    right = mid-1;
        }
        return left;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

🐳35. 搜索插入位置

🌼题目

题目链接：35. 搜索插入位置 - 力扣（LeetCode）

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为O(log n)的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2
1
2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1
1
2

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4 
1
2

提示:

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums 为 无重复元素 的 升序 排列数组
• -104 <= target <= 104

🌻算法原理

本题要求是如果找到目标值，则返回下标；如果找不到，则返回要填入的位置

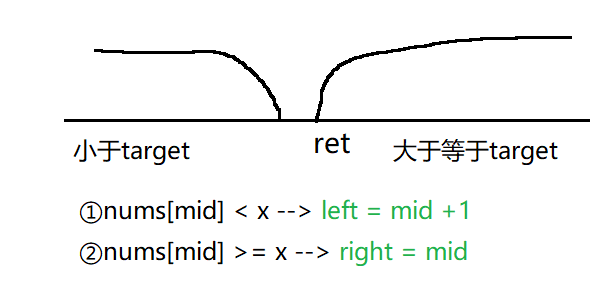
🌷代码实现

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size()-1;
        while(left < right)
        {
            int mid = left + (right-left)/2;
            if(nums[mid] < target)  left = mid+1;
            else    right = mid;
        }
        if(nums[left]<target)   return left+1;
        return left;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

🦭852. 山脉数组的峰顶索引

🌼题目

题目链接：852. 山脉数组的峰顶索引 - 力扣（LeetCode）

符合下列属性的数组 arr 称为 山脉数组 ：

• arr.length >= 3
• 存在i（0 < i < arr.length - 1）使得：
  • arr[0] < arr[1] < ... arr[i-1] < arr[i]
  • arr[i] > arr[i+1] > ... > arr[arr.length - 1]

给你由整数组成的山脉数组 arr ，返回满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i 。

你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。

示例 1：

输入：arr = [0,1,0]
输出：1
1
2

示例 2：

输入：arr = [0,2,1,0]
输出：1
1
2

示例 3：

输入：arr = [0,10,5,2]
输出：1
1
2

提示：

• 3 <= arr.length <= 105
• 0 <= arr[i] <= 106
• 题目数据保证 arr 是一个山脉数组

🌻算法原理

题目说了，这些数据必是一个山峰数组，所以我们可以直接暴力的将其遍历，找出前一个数小于当前数的位置，但有个要求是时间复杂度为O(log(n)) 。

由于这个数组必是山峰数组，那么它是具有二段性的，所以我们可以采用二分查找

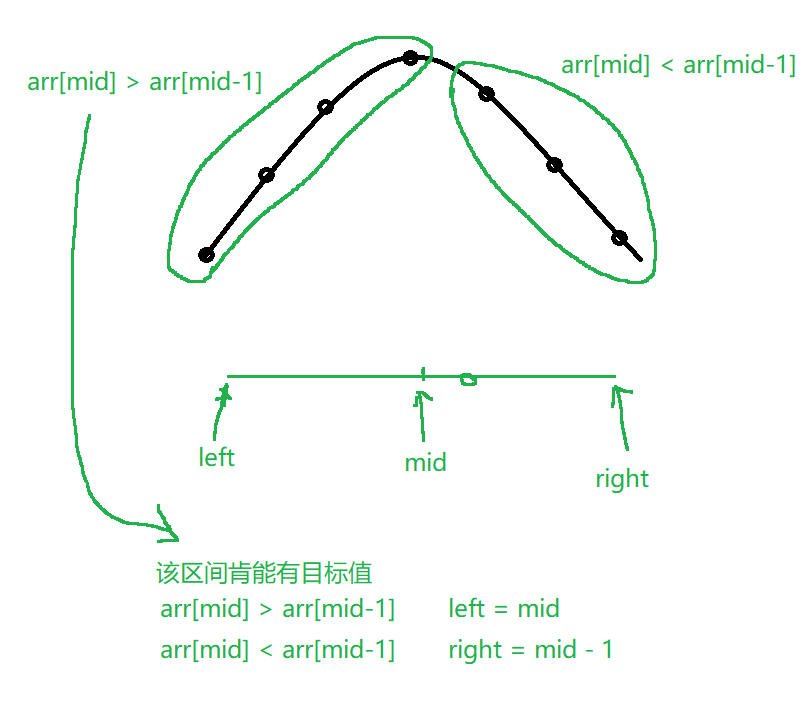
代码实现

class Solution {
public:
    int peakIndexInMountainArray(vector<int>& arr) 
    {
        int left = 1;   //初始位置和末尾位置必不可能是峰顶
        int right = arr.size()-1 -1;
        while(left < right)
        {
            int mid = left + (right - left + 1) / 2;
            if(arr[mid] > arr[mid-1])	left = mid;
            else	right = mid-1;
        }
        return left;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

🐧162. 寻找峰值

🌼题目

题目链接：162. 寻找峰值 - 力扣（LeetCode）

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

示例 1：

输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。
1
2
3

示例 2：

输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5 
解释：你的函数可以返回索引 1，其峰值元素为 2；
     或者返回索引 5， 其峰值元素为 6。
1
2
3
4

提示：

• 1 <= nums.length <= 1000
• -231 <= nums[i] <= 231 - 1
• 对于所有有效的 i 都有 nums[i] != nums[i + 1]

🌻算法原理

我们可以暴力解法，遍历这个数组，如果开始下降，则可以返回该位置的值；如果一直向上，则返回最后一个位置的即可。这里最坏的情况就是走到最后一个位置，时间复杂度为O(N)。

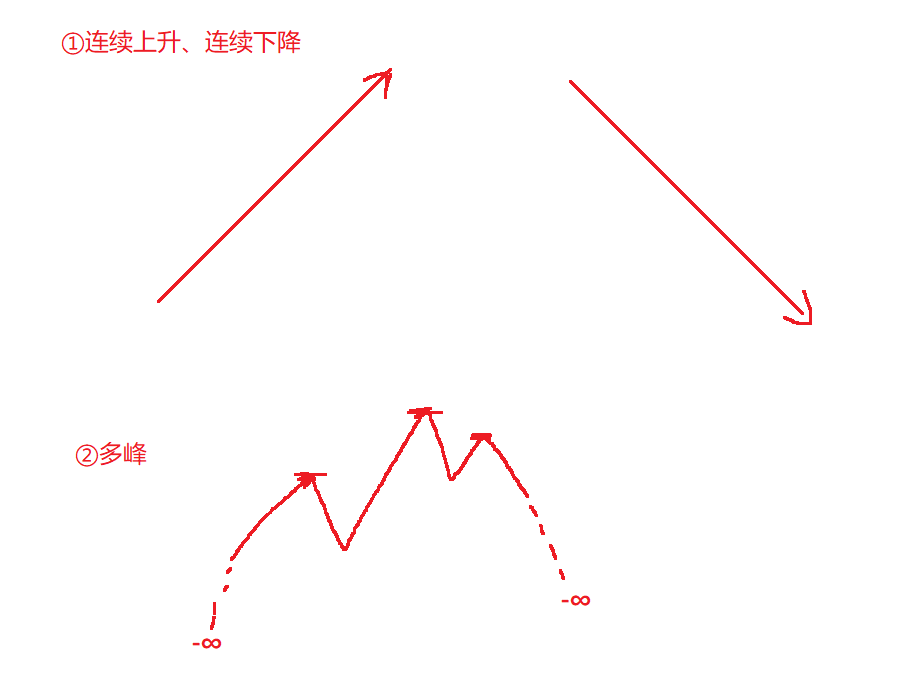
在此基础上，我们可以优化这个暴力解法，我们抽象这个数组：

• 选定某i位置，当前位置大于i+1，此时是一个下降区域，那么在i的左边区域，肯定会有一个上升区域（因为左右都是负无穷），而右边区域不一定有结果，因为右边也是负无穷，可能会一直下降到负无穷大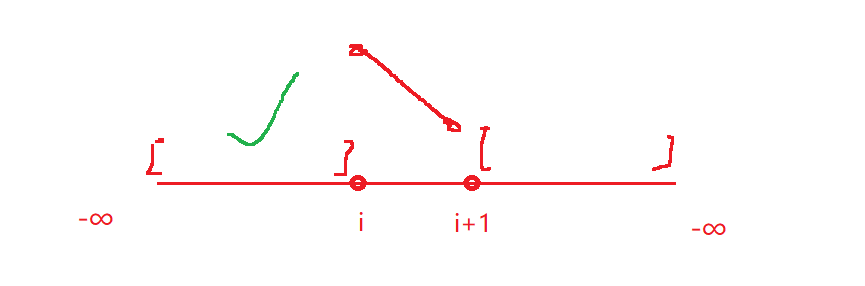

  

• 如果选的的i位置，小于i+1位置的元素，那么这个区域此时是一个上升区域，那么在i的右边区域，肯定会有一个下降区域
  

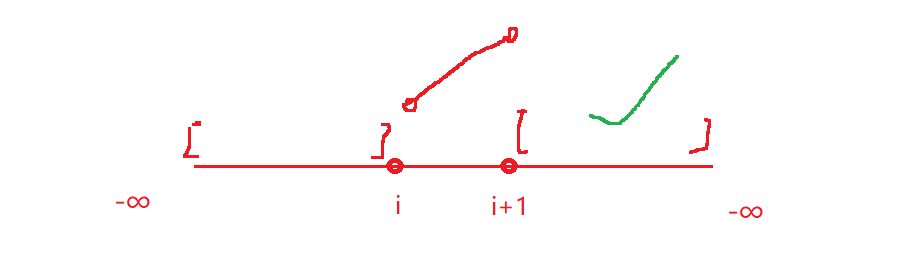
通过这两种情况的抽象，虽然这个数组是一个完全无序的数组，但是它具有二段性，那么我们就可以采用二分查找的思想

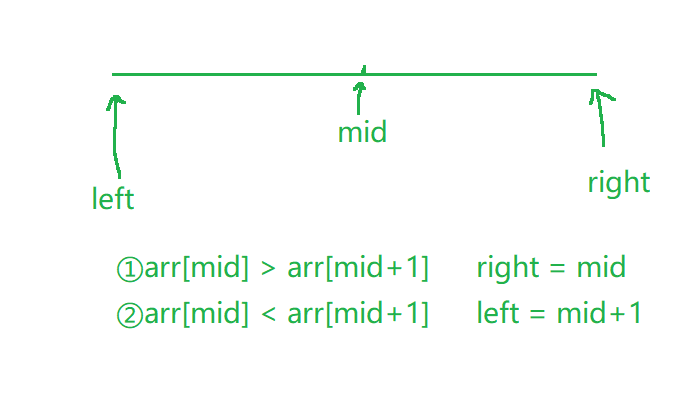
🌷代码实现

class Solution {
public:
    int findPeakElement(vector<int>& nums)
    {
        int left = 0;
        int right = nums.size()-1;
        while(left < right)
        {
            int mid = left + (right-left)/2;
            if(nums[mid] > nums[mid+1])
                right = mid;
            else
                left = mid+1;
        }
        return left;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

🦚153. 寻找旋转排序数组中的最小值

🌼题目

题目链接：153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
• 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。
1
2
3

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。
1
2
3

示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。
1
2
3

提示：

• n == nums.length
• 1 <= n <= 5000
• -5000 <= nums[i] <= 5000
• nums 中的所有整数 互不相同
• nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

🌻算法原理

这就只有一个数组，我们可以直接暴力求解，直接遍历整个数组，找出最小值，直接遍历的时间复杂度为O(N)。

由于题目说这是一个预先有序的数组，旋转得到的，所以这个数组是有二段性的

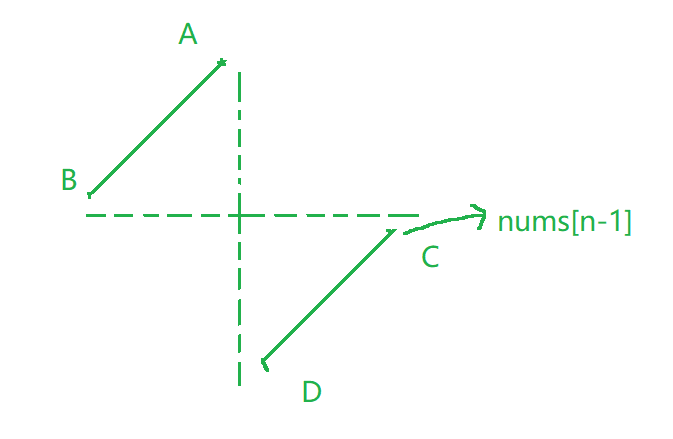
• 在A~B区域：nums[i] > nums[n-1]
• 在C~D区域：nums[i] <= nums[n-1]

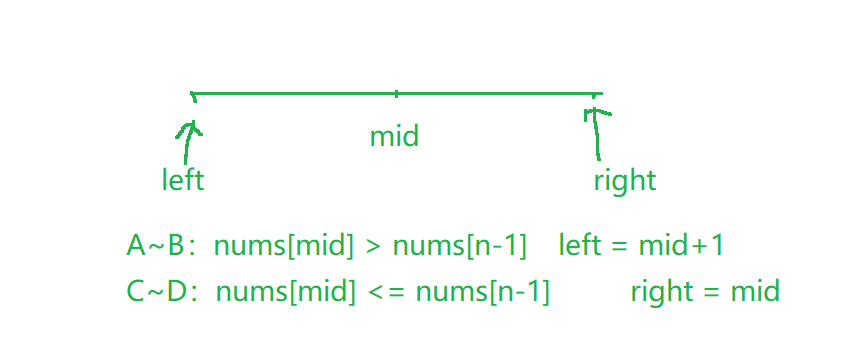
🌷代码实现

class Solution {
public:
    int findMin(vector<int>& nums)
    {
        int left = 0;
        int right = nums.size()-1;
        int t = nums[right];
        while(left<right)
        {
            int mid = left+(right-left)/2;
            if(nums[mid]>t)
                left = mid+1;
            else
                right = mid;
        }
        return nums[left];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

🦖LCR 173. 点名

🌼题目

题目链接：LCR 173. 点名 - 力扣（LeetCode）

某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组 records。假定仅有一位同学缺席，请返回他的学号。

示例 1:

输入: records = [0,1,2,3,5]
输出: 4
1
2

示例 2:

输入: records = [0, 1, 2, 3, 4, 5, 6, 8]
输出: 7
1
2

提示：

1 <= records.length <= 10000
1

🌻算法原理

这题还是比较简单，但是有很多种方法

1. 哈希表
2. 直接遍历
3. 位运算
4. 高斯求和

这四种解法，时间复杂度都是O(N)

该题目说，学号从0开始，那么在断开之前，整个数组对应的下标和元素是相等的，从断开位置开始，元素都是比下标大1的，这又出现了二段性，那么就可以采用二分查找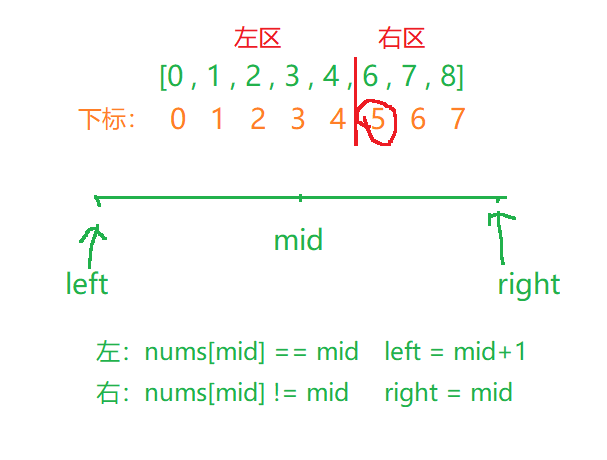

有可能整个数组完全不缺，例如0,1,2,3那么我们缺少的就是4，所以最后还需要处理边界情况

🌷代码实现

class Solution {
public:
    int takeAttendance(vector<int>& records) {
        int left = 0;
        int right = records.size()-1;
        while(left < right)
        {
            int mid = left + (right - left)/2;
            if(records[mid] == mid)
                left = mid+1;
            else
                right = mid;
        }
        return records[left]==left?left+1:left;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16