-
现代计算与光学的跨界机遇——

时至今日,互补氧化金属半导体(CMOS)技术的飞速发展促进了集成电路的空前成功。

晶体管的创新与时俱进
正如戈登-E-摩尔(Gordon E. Moors)在1965年预测的那样,每隔18-24个月,计算芯片上的晶体管数量就会翻一番。此外,罗伯特·丹纳德(Robert H. Dennard)的缩放法则解释了进一步缩小晶体管尺寸的好处。如今,摩尔定律已使中央处理器(CPU)的速度比1990年提高了超300倍。然而,正如国际半导体技术路线图(ITRS)在2016年预测的那样,这种惊人的发展是不可持续的。在5纳米技术节点之后,半导体行业很难再向前发展。此外,人工智能(AI)应用的激增产生了指数级增长的数据量,传统计算系统和架构难以处理这些数据。这种令人绝望的差异推动了对数据处理新方法和替代架构的大量研究。
与电子设备相比,光学设备可以在瞬间处理信息,且能耗和发热量几乎可以忽略不计。此外,通过采用波分复用(WDM)和模分复用(MDM)等复用方案,光学设备在数据处理方面的并行性比电子设备好得多。由于采用了光的特性,许多复杂计算系统的架构和布局都有可能通过引入光计算单元而得到简化。
一般来说,光计算可分为两类:数字光计算和模拟光计算。基于布尔逻辑的数字光计算采用与基于晶体管的通用计算类似的机制,已经发展了30多年。然而,由于光器件的集成密度较低,传统的数字计算难以胜任。相比之下,模拟光计算利用光的物理特性(如振幅和相位)以及光和光器件之间的相互作用来实现某些计算功能。它是一种专用计算,因为在某个模拟光计算系统中对计算过程进行了独特的数学描述。与传统的数字计算相比,模拟光学计算在模式识别和数值计算等特定任务中可以实现更好的数据处理加速。
因此,作为后摩尔时代最有前途的计算技术之一,模拟光计算系统吸引了大量的研究工作。

摩尔定律和丹纳德缩放规则(Dennard’s scaling rules)最初表明,缩小晶体管尺寸是在不增加能量消耗的情况下提高计算能力的可行方法。然而,CMOS技术的不断发展导致了丹纳德缩放规则的失效,因为缩小的晶体管无法保持恒定的能量密度。

在CPU中使用更高的时钟频率(clock frequency)是进一步提高计算能力的另一种可行方法。然而,采用高时钟频率后,功耗产生的热效应将成为CPU性能的新瓶颈。如今,在5GHz时钟频率的限制下,CPU的计算能力可通过采用并行架构来提高。
除了功率耗散产生的热效应,制造工艺的限制也对摩尔定律提出了挑战。为了扩大CPU晶体管的缩小规模,应在当前的生产线中引入新的自上而下图案化方法。波长为13.5纳米的极紫外(EUV)光刻技术是扩展摩尔定律的核心技术,因为波长更短,分辨率更高。对于超紫外干涉光刻技术而言,半间距的理论极限约为3.5纳米。同样,电子束光刻(EBL)作为另一种制造技术,也能以高分辨率制造集成电路的极细图案。虽然电子束光刻技术能提供接近原子级的超高分辨率,并能适应各种材料,但其加工时间比光学光刻技术更长、成本更高。
这些用于硅基CMOS电路的缩小方法被归类为“更摩尔”(More Moore)技术,用于维持摩尔定律。然而,在采用更好的制造技术缩小晶体管栅极沟道尺寸后,量子效应(如量子隧穿和量子散射)将带来其他不可预知的问题。例如,在最新的亚5纳米全栅极(GAA)鳍式场效应晶体管(FinFET)中,由于量子效应,有效鳍宽度减小,阈值电压升高。
因此,不断缩小晶体管尺寸将无法持续提高计算能力。
除了摩尔定律的物理限制带来的挑战外,传统数字系统的计算能力也受到了蓬勃发展的人工智能应用的挑战。最流行的人工智能实现是深度神经网络(DNN),其中包含两种最重要的类型:卷积神经网络(CNN)和长短期记忆(LSTM)。在CNN中,有一系列卷积层和子采样层,然后是全连接层和归一化层。卷积是推理的主要计算任务,反向传播仅用于训练CNN中的所有参数;LSTM由存储单元块组成,由输入、遗忘和输出门决定,LSTM块的输出通过单元值计算。
为了提高输出结果的准确性,DNN开发了大量参数。第一个DNN模型LeNe仅包含5个卷积层和60K个参数。2012年,AlexNet成为性能最好的DNN模型,拥有60M个参数。如今,Megatron模型包含3.9G个参数,需要数周时间进行训练,成本高达数百万美元。
上述DNN的所有过程都包含许多复杂的计算任务,需要消耗大量的计算资源。OpenAI研究的一项指标显示,从2012年到2018年,人工智能的繁荣对计算能力的需求增加了30多万倍,而摩尔定律仅能带来7倍的提升。
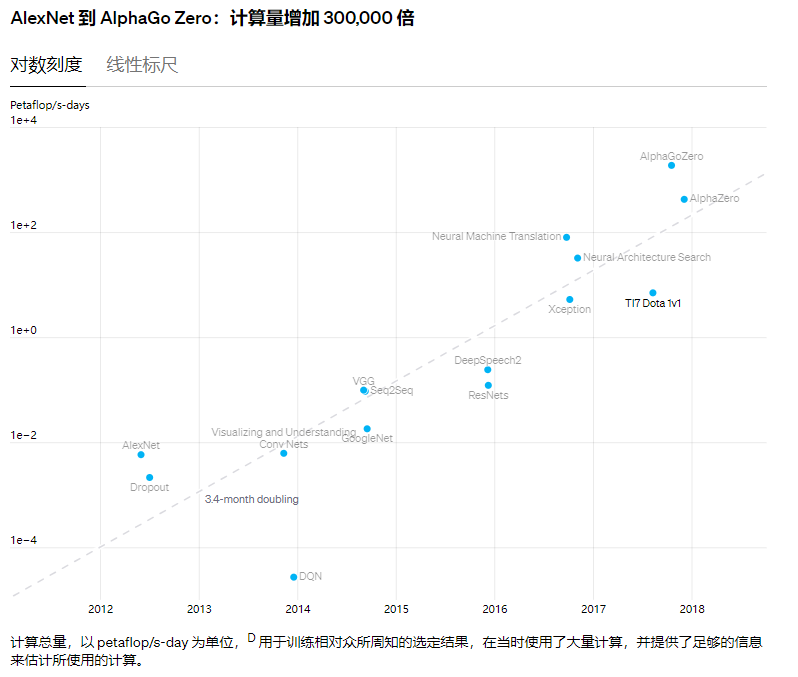
简而言之,人工智能应用变得越来越复杂、精确,计算资源也越来越枯竭;为了应对这些挑战,人们对更高计算能力的系统有着极大的渴求。
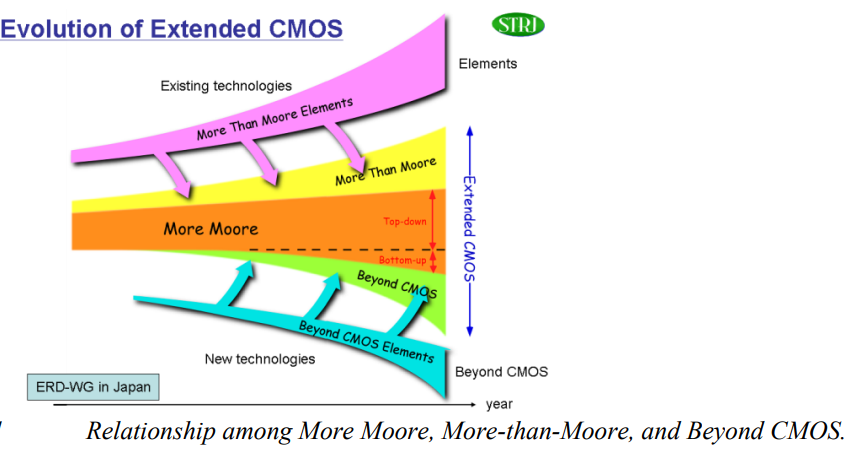
显然,扩展摩尔定律是获得计算能力的一个关键因素。为了促进半导体技术的发展,除了“More Moore”之外,还有“More than Moore”和“Beyond CMOS”两条技术路线。“More Moore”包括利用各种技术(如片上系统、封装系统、片上网络等)设计复杂的异构系统,以满足特定需求和高级应用。“Beyond CMOS”探讨了提高CMOS晶体管性能的新材料,如碳纳米管(CNT)。由于碳纳米管既可以是金属也可以是半导体,因此分离纯半导体纳米管对于制造高性能晶体管至关重要。然而,如何纯化和可控定位这些直径为1纳米的分子圆柱体仍是当今面临的一项艰巨挑战。
除了扩展摩尔定律,开发新的系统架构还能提高传统数字系统的计算能力。在基于CMOS的静态随机存取存储器(SRAM)中,人们对内存计算架构进行了广泛的探索。然而,CMOS存储器的密度有限,扩展趋势缓慢。研究人员开始利用新兴的非易失性存储器(NVM)技术探索内存计算架构,如相变材料(PCM)和电阻式随机存取存储器(RRAM)。NVM器件以二维横条阵列的形式配置,由于NVM器件允许非易失多状态,因此可以实现高性能计算。NVM交叉条可以并行执行乘法运算,与传统的数字加速器相比,省去了数据传输,因此能效更高、速度更快。高密度NVM横条可提供大规模并行乘法运算,从而引发了对模拟内存计算系统的探索。
上述方法似乎仍无法应对计算复杂度极高的应用所带来的挑战,如大规模优化、大分子模拟、大数分解等。这些应用需要大量内存,而最强大的超级计算机也难以满足这些要求。此外,处理这些应用还需要几十甚至更长的运行时间。
因此,研究有别于基于布尔逻辑和冯-诺依曼架构的传统计算系统的新计算模式至关重要。目前,被称为物理计算范式的量子计算、DNA计算、神经形态计算、光学计算等正引起越来越多研究人员的关注。这些物理计算范式在设备层面提供了比布尔逻辑更多的复杂度算子,可用于构建卓越的加速器。
与量子计算的低温要求、DNA 和神经形态计算的动态不稳定性相比,光计算具有宽松的环境要求和坚实的系统组成。因此,光计算被认为是解决棘手问题的最有前途的方法之一。

光计算并不是一个全新的概念。
早在二十世纪中叶,人们就已经发明了光相关器,它可以被视为光计算系统的初步雏形。以傅立叶光学原理为基础的其他技术,如4F系统和矢量矩阵乘法器 (VMM),在上世纪也得到了很好的发展和研究。
数字电子计算机的巨大成功促进了对数字光学计算机的研究,其中的光学逻辑门已被串联起来 。由于光子具有高带宽、发热量可忽略不计和响应速度超快等固有优点,用光晶体管取代电晶体管的想法被认为是制造数字光计算机的一种有竞争力的方法。
然而,自二十世纪中叶以来,这一诱人的想法尚未得到系统的验证。米勒(D. B. Miller)在2010年提出了光逻辑的一些实用标准,并指出目前的技术无法满足这些标准。这些标准包括逻辑级还原、级联性、扇出、输入输出隔离、无临界偏置和逻辑级独立损耗。
直到现在,数字光学计算机仍然是一个令人神往的蓝图。由于兼容性和灵活性,数字电子计算机仍然是一种实用可靠的系统。另外,利用物理机制的模拟光计算为光计算开辟了新的可能性,因为它通过实现算术运算而不是布尔逻辑运算,降低了对高集成度的要求。
1)光域中的矢量和矩阵操作
由于光计算作为一种通过逻辑运算实现通用计算的可行方法尚未得到验证,人们开始探索乘法和加法等算术计算的潜在机会。
第一个扇入/扇出VMM早在1978年就已提出。该乘法器用于计算矢量和矩阵之间的乘法运算,如下所示:
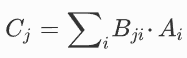
其中,A和B分别是向量和矩阵。

光学向量矩阵乘法器。(a)传统的自由空间扇入扇出 VMM 方案;(b)SVD分解。这里,V、Σ和U分别代表单元矩阵、对角矩阵和单元矩阵。(c)基于波分复用和微环阵列的VMM芯片方案。(d)由片上微梳和PCM调制器矩阵实现的VMM方案
此外,得益于快速发展的硅基液晶(LCoS)技术和显示器行业的推动,SLM或DMD的分辨率变得相当高(4K分辨率已投入商用)。但是,串扰误差是利用高分辨率SLM或DMD展示VMM最大性能的主要障碍。虽然串扰问题可以通过扩大SLM或DMD的像素尺寸来解决,但SLM或DMD的功能区限制了矩阵的尺寸。同时,即使使用非相干光源,光的衍射问题也不容忽视。这种限制被称为空间-带宽积,类似于传统通信系统中的时间-带宽积。
近年来,许多创造性的工作都是在波导中而不是使用传统的自由空间VMM方案中提出和演示的。米勒(D. B. Miller)提出了一种有效设计通用线性工作光学元件的方法,可通过马赫-泽恩德干涉仪(MZI)阵列实现。Shen和Harris等人利用可编程纳米光子处理器芯片展示了一种深度学习神经网络。如上图(b)所示,该芯片由56个MZI组成,作为一个光干涉单元(OIU)工作,有4个输入端口和4个输出端口。
后来,Shen和Harris分别成立了初创公司Lightelligence和Lightmatter,将这一论文工作进一步推向商业应用。2020 年,Lightmatter在HotChips论坛上发布了名为“Mars”(火星)的电路板设备演示,其中集成了光电混合芯片和其他配套电子元件。

除了使用MZI阵列和SVD方法外,还有其他芯片架构可以支持直接矩阵加载。
这些架构类似于谷歌TPU(张量处理单元)中的收缩阵列和内存计算领域的“横杆”设计。在上述架构中,不同类型的调制器可以在很大程度上取代MZI实现乘法运算。同时,光微栅的波长选择性也可以消除不同波长数据之间的串扰。
VMM是一种通用算子,可用于完成复杂的计算任务,如傅立叶变换和卷积,但需要消耗更多的时钟周期。然而,利用光子固有的并行性,这些复杂的计算任务可以在一个“时钟周期”内完成。
从理论上讲,相干光波经理想透镜变形的过程与FT的过程是等价的。基于这一概念,4F系统可用于进行卷积处理。由于卷积是CNN中最沉重的负担,韦茨斯坦(Gordon Wetzstein)等人在基于4F系统的光电混合CNN中进行了有益的探索。通过精心设计4F系统的有效点扩散函数,将训练好的CNN网络的权重加载到多个无源相位掩模上。在 MNIST、QuickDraw和CIFAR-10标准数据集进行分类时,准确率分别达到了90%、78%和45%。

光学计算中的复杂矩阵操作。两个灰条分别代表输入数据(A)和卷积结果(C)。凸透镜是实现傅立叶变换的傅立叶透镜。(b)基于色散效应的光学卷积处理器示意图。(c)具有多层被动衍射平面的衍射深度神经网络示意图
除了上述基于4F的方案外,还有其他替代方法来实现光学中的FT和卷积。由于传统透镜是一种笨重的设备,几种类型的有效透镜,如梯度指数技术、元表面和反设计的衍射结构,因其微型化的特点,被认为是实现FT的替代设备。然而,基于这些新方法的计算精度尚未得到充分利用。
除了基于傅立叶透镜的空间域FT实现外,FT还可以在考虑串行数据输入的情况下在时域实现。例如,多波长光在色散介质中传播时产生的色散效应可以被视为实现FT过程的“时间透镜”。最近,通过分别在波长域和时域加载权重数据和特征图数据,这一方案被进一步用于CNN协同处理。
2018年,奥兹坎(Aydogan Ozcan)等人为光学机器学习提出了一种名为衍射深度神经网络(D2NN)的新网络。这种光学网络由多个衍射层组成,其中给定层上的每个点就像一个神经元,具有复值传输系数。虽然激活层尚未实现,但在0.4THz下进行的实验测试结果相当不错,对MNIST和Fashion-MNIST的分类准确率分别为91.75%和81.1%。
一年后,数值工作表明,MNIST和Fashion-MNIST数据集的准确率分别提高到了98.6%和91.1%。此外,这项工作还证明灰度CIFAR-10数据集的准确率为51.4%。除了对MNIST和CIFAR的分类,改进后的D2NN在突出物体检测(数值结果,视频序列的F测量值为0.726)和人类动作识别等方面的能力也得到了证明。
2)光储备池计算(Reservoir Computing)
储备池计算(Reservoir Computing)源于液态机(LSM:Liquid state machines)和回声状态网络(echo state network,ESN)的概念,是一种源自递归神经网络(RNN)[68]的新型计算框架。
它由三层组成,分别称为输入层、存储层和输出层。与使用反向传播训练的一般RNN(如LSTM和门控递归单元(GRU))不同,RC只需要针对特定任务训练从储层到输出层的读出系数(Wout表示)。内部网络参数,即从输入层到储层的邻接矩阵Win以及储层内部的连接W是未经训练的,它们是固定和随机的或规则拓扑。在传统储层计算架构的训练阶段,储层状态是在每个离散时间步长n以下收集的:
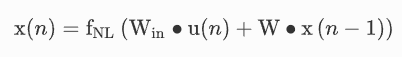
其中,fNL是矢量非线性函数,u(n)是输入信号,x(n)是储备池状态。在监督学习的情况下,最优读出矩阵Wout可通过脊回归求得,一般如下:
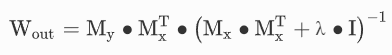
其中,Mx是由储备池状态x与一些训练输入向量u连接而成的矩阵,My是由与训练输入向量相对应的地面实况连接而成的目标矩阵,I是标识矩阵,λ是正则化系数,用于避免过度拟合。在测试阶段,预测输出信号y(n)的计算方法如下:
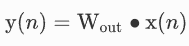
与一般的RNN相比,RC的训练时间缩短了几个数量级,大大加快了取得成果的时间。此外,RC在许多连续任务中都达到了最先进的性能。最后但同样重要的是,RC对硬件实现非常友好。由于上述优点,RC在研究界受到越来越多的关注:它已被用于信号均衡、时间序列预测或分类,以及时序去噪。
关于RC的研究主要集中在三个方面:RC应用范围的扩展、储备池拓扑结构的优化和新的物理实现。第一个方面致力于利用RC解决特定任务;第二个方面旨在降低RC算法的计算复杂度或增加内存容量;第三方面是采用新的机制来实现或优化RC。
光子技术因其固有的并行性和速度,非常适合RC的硬件实现。近十年来,RC的光电/光学实现引起了研究人员的极大兴趣。根据实现储层内部连接的方式,光电/光RC可分为两类:空间分布式RC(SD-RC)和延时RC(TL-RC)。

标准RC布局和空间分布式RC方案
对于SD-RC,它可以实现储层的各种连接拓扑。2008年,范多尔内(Kristof Vandoorne)等人在数值模拟中提出在半导体光放大器(SOA)的片上网络中实现光子RC,SOA以瀑布拓扑结构连接,SOA的功率饱和行为类似于非线性函数。不久之后,研究人员意识到将SOA驱动到功率饱和结果的能效很低,打算用光学方法重现数值模拟的性能。因此,范多尔内等人提出并在硅光子芯片上演示了RC,该芯片由光波导、光分路器和光合路器组成,如上图(b)所示。存储节点用彩色圆点表示,蓝色箭头表示网络拓扑结构。非线性是通过光检测器实现的,因为光检测器检测的是光功率而不是振幅。这种方法可处理速率为0.12至12.5Gbit/s的数据。
2015年,布伦纳(Daniel Brunner)等人展示了一种空间扩展光子RC,它基于垂直腔面发射激光器(VCSEL)的衍射成像,使用标准衍射光学元件(DOE)。储层中的连接矩阵是通过VCSEL单个激光器之间的耦合实现的,其中每个激光器的偏置电流可单独控制。如上图(c)所示,VCSEL阵列的图像在成像透镜的左侧形成。通过对系统参数进行微调,在通过DOE分束器后,一个激光器的衍射阶数将与相邻激光器的非衍射图像重叠,从而实现不同神经元的连接。
对于TL-RC,由于单根延迟线的环形对称性,形成了一个具有环形连接拓扑结构的离散储备池。它只使用一个具有延迟反馈的非线性节点。从本质上讲,TL-RC构成了空间与时间之间的交换。在输入层,使用时间输入掩码Win将输入信息u(n)映射到TL-RC的时间维度,从而得到N维向量:
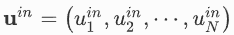

基于TL-RC计算机的总体结构
继一些开创性工作之后,基于光电振荡器的TL-RC已在各种任务中进行了测试,这些任务可分为两大类:分类和预测。除光电实现外,TL-RC的另一个分支是全光RC。在这一分支中,非线性节点由光学元件实现,如半导体光放大器、半导体可饱和吸收镜、外腔半导体激光器和垂直腔面发射激光器。
光/光电子实现RC的主要优点是低功耗和高处理速度,这源于并行性和光速。在商业应用之前,系统的集成化或微型化是光电/光学RC需要解决的主要挑战;更重要的是,光电/光学遥控的杀手级应用亟待验证。
3)光子伊辛机
许多重要应用,如电路设计、路线规划、传感和药物发现,都可以用组合优化问题来进行数学描述。众所周知,许多此类问题都是非确定性多项式时间(NP)-hard或NP-complete问题。
然而,用传统(冯-诺依曼)计算架构来解决这些NP问题是计算机科学领域的一个基本挑战,因为计算状态的数量会随着问题规模的增大而呈指数增长。这一挑战促使大量研究工作试图开发非冯-诺依曼架构。幸运的是,伊辛模型通过搜索伊辛哈密顿的基态,为高效解决这些计算困难的问题提供了可行的方法。
在不同的物理系统中,如超导电路、俘获离子、机电振荡器、CMOS器件、忆阻器、极化子和光子系统种,已经提出并在实验中证明了各种模拟伊辛哈密顿的方案。在这些系统中,光子系统因其固有的并行性、低延迟和几乎不受环境噪声(即热噪声和电磁噪声)影响等独特特性,被认为是最有前途的候选系统之一。

光学伊辛机概述。(a)伊辛模型。(b)基于退化OPO的相干伊辛机 (CIM) 示意图。(c)伊辛机在调制器的非线性状态下工作。(d)基于多光纤的伊辛机。(e)基于SLM的模拟退火
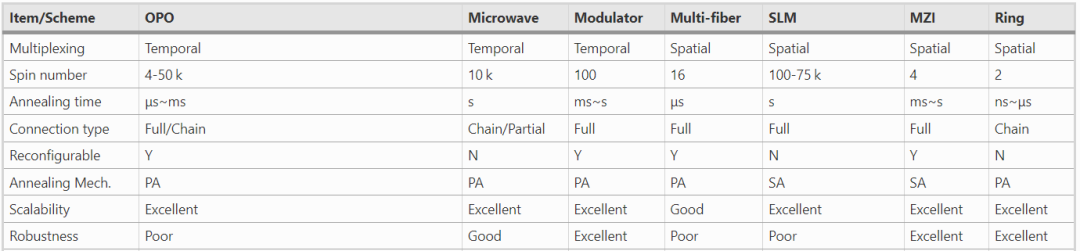
不同方案的实验数据
上表总结了相关工作的实验数据。这些实验演示可分为三类:基于光纤的系统、自由空间系统和基于芯片的系统。
基于光纤的系统的每个自旋节点由一个光脉冲表示,它们之间的相互作用网络由光延迟或现场可编程门阵列(FPGA)实现。基于光纤的系统的一个优点是具有出色的可扩展性,可以通过增加腔长或重复率来建立大规模伊辛模型,但由于光子的相干时间相对较短,因此存在鲁棒性问题。一种缓解方法是在微波信号中编码自旋态,因为微波信号的相干时间远远长于光信号。此外,时间多路复用方案限制了其应用范围,因为顺序处理会牺牲大部分退火时间。
自由空间系统的自旋节点和交互网络分别由光纤芯(或像素)和SLM实现。在空间域,自由空间系统可同时实现大规模伊辛模型退火。然而,实际环境中不可避免的波动会破坏相互作用网络,因为它依赖于精确的对准。基于芯片的系统的相互作用网络由MZI矩阵实现,而自旋节点可以通过可扩展的构件来构建,如微环谐振器。
得益于先进的CMOS技术,基于芯片的系统有可能将一个笨重的系统缩小为一个单片/混合芯片,使其几乎不受环境波动的影响。与其他两类系统所展示的自旋节点相比,芯片系统是PIM方法中的“丑小鸭”。
基于这些广泛的研究工作,PIM的技术路线图正变得非常清晰:就是开发一种高度可扩展、可重构和鲁棒的PIM,它能在多项式时间内找到大规模组合优化问题的最优(或接近最优)解。
总体来说,PIM在过去十年中取得的可喜成果表明,它是解决计算难题的可行途径。然而,这一研究方向还需要持续的研究努力,以构建一个可扩展、可重构和稳健的PIM,从而对我们的社会产生深远的影响。

模拟光计算被认为是后摩尔时代执行复杂计算的另一种方法。与电子计算相比,光计算的一个突出优势是在光域执行乘法运算时,能耗可以忽略不计。然而,这种光电混合系统的实际效益还需要系统分析,尤其是在不同域和格式之间传输数据的成本尚未得到讨论。
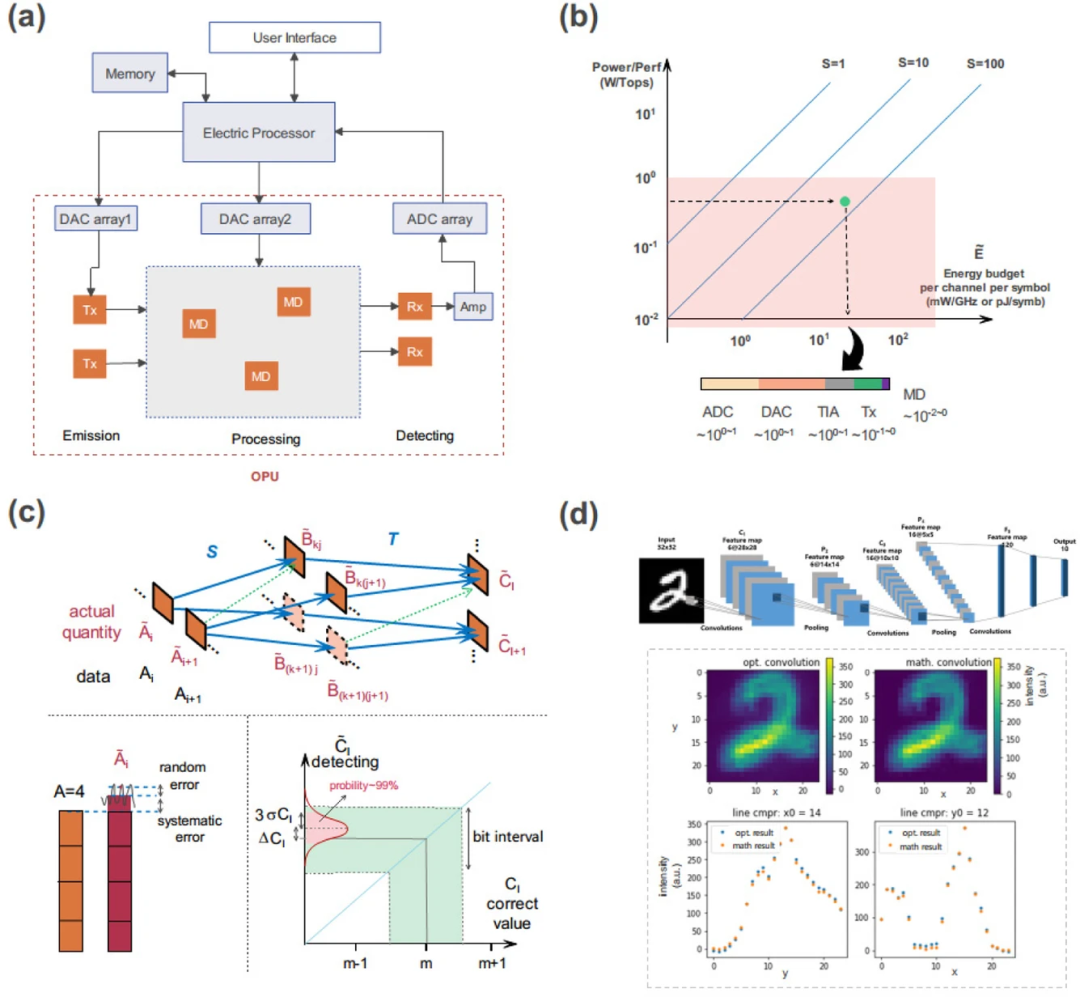
光电混合计算系统概览。(a)光电混合系统结构示意图;(b)功率成本与性能之比;(c)OPU有限精度分析示意图
根据上述讨论,光计算的各种方法面临着一些普遍挑战。首先,为了提高光计算系统在硬件层面的并行性,我们亟需大规模集成光电芯片的制造技术。此外,还需要光电协同封装技术来降低电域和光域之间的数据传输成本。
其次,现代光发射器和调制器是为光通信而非计算任务而设计的。例如,在大多数应用中,光计算系统对光器件消光比和线性度的要求远远高于光通信,因为大多数应用的输入数据都是高比特深度的。光器件的消光比和线性度越高,就越能支持数据输入的高效光编码,系统吞吐量也就越高。
第三,新的架构设计必不可少。传统的计算架构很难发挥光计算的优势,因为光电转换会严重限制混合计算系统的能效。新的架构设计可以具有较大的加速因子S(即用较少的有源器件处理更多的操作),同时尽可能保留可配置性。
最后,适用于模拟光计算的算法探索还很少。目前,算法的设计基于布尔逻辑,适用于数字计算系统。然而,这些算法很难与光学计算所提供的算子相匹配。如果开发出适用于光学计算的算法,其运算复杂度和执行时间将大大短于目前的算法。
虽然面临诸多挑战,但光学计算的机遇也在不断增加。首先,在开发更大规模的光电集成芯片方面,已经有许多制造技术参与其中。例如,Lightmatter曾公司发布了全球首款4096MZI集成芯片“火星”,证明了大规模集成的可行性,为光计算研究人员带来了更多信心。此外,前面提到的波分复用(WDM)和多波分复用(MDM),以及空间光学系统的兼容,也有利于并行性的提高。
其次,光器件的低消光比和线性度可以通过直接使用低比特深度光编码的高速光器件来弥补。例如,使用OOK的2GHz光调制器和使用PAM4的1GHz光调制器在数据输入效率上是相当的。然而,这种补偿只在某些计算过程中可行,这些计算过程可以转换为时域中一系列低比特深度操作的线性组合。相比之下,对应用的输入数据进行低位深度量化是现代光学设备在光学计算中实用化的普遍解决方案。
第三,为了减少混合计算系统中光电转换的开销,需要充分利用光信号循环,尽可能长时间地将数据保留在光域中。由于光的传播速度快,光信号循环所造成的时间延迟可以忽略不计——流处理方法可以为新架构提供灵感。
最后,为光计算开发的算法可以考虑光域中提供的复杂算子。当前算法中的一些布尔逻辑算子集可以用一个复杂算子来代替,从而降低复杂度,缩短执行时间。因此,将复杂算子与布尔逻辑算子结合到算法中是开发适用于光学计算的算法的潜在途径。
显而易见的是,光学计算的机遇正在不断增加。人工神经网络及其计算饥渴症的需求不断增长,将持续推动光计算模式的研究;光传感和光通信可能会给光计算带来另一个应用机会。此外,光域中的高复杂度计算方法,如傅立叶变换、卷积和方程求解等,可以有效提高系统效率。总之,光计算被认为是后摩尔时代的“灵丹妙药”。
要将模拟光计算推广到实际应用中,需要从根本上解决大规模集成技术、合适的器件和合适的算法等问题。坦率地讲,后摩尔时代光计算的机遇正在增多,光计算的前景十分广阔。
参考链接:
[1]https://www.intel.com/content/www/us/en/newsroom/resources/moores-law.html
[2]https://photonix.springeropen.com/articles/10.1186/s43074-021-00042-0#change-history
[3]https://openai.com/research/ai-and-compute
[4]https://www.semiconductors.org/wp-content/uploads/2018/08/2011ERD.pdf
-
相关阅读:
数据结构01
工作项目:我要买G!T!R!
UG NX二次开发(C++)-采用std::vector对体对象的质心进行排序
算法:动态规划的入门理解
图片批量修改尺寸如何实现?
求你了,别在高并发场景中使用悲观锁了!
CSAPP 之 BombLab 详解
【最全日期获取合集】js获取昨天,今天,明天,上周,本周,下周,上月,本月,下月,去年,本年,明年,上季度,本季度,下季度,向前推日期等【全覆盖,拿来即用】
对比CentOS与Ubuntu:选择最适合你的Linux发行版
3D科研绘图与学术图表绘制:从入门到精通
- 原文地址:https://blog.csdn.net/QUANTUM_CHINA/article/details/134558472