-
SO3 与so3 & SE3与se3 & SIM3
1 旋转*叉乘
1.1 旋转矩阵的导数
根据旋转矩阵的性质: R R T = I RR^T=I RRT=I,对两侧进行求导可得:
R ˙ R T = − R R ˙ T \dot{R} R^T=-R\dot R T R˙RT=−RR˙T
从而可知, R ˙ R T \dot R R^T R˙RT为一个反对称对阵,则存在向量 ω ω ω,使得 R R ˙ T = ω ^ R \dot R^T=\hat ω RR˙T=ω^ω ^ = [ 0 − ω z ω y ω z 0 − ω x − ω y ω x 0 ] \hat \omega =\left[
\right] ω^= 0ωz−ωy−ωz0ωxωy−ωx0 0 − ω z ω y ω z 0 − ω x − ω y ω x 0
即: R ˙ = ω ^ R \dot R =\hat ωR R˙=ω^R1.2 物理意义
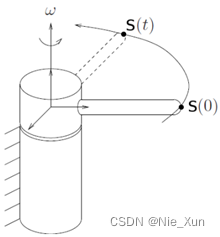
设空间一个点 S ( t ) S(t) S(t),其绕空间某个轴旋转,设其在t时刻的旋转轴为 ω ( t ) / ‖ ω ( t ) ‖ ω(t)/‖ω(t)‖ ω(t)/‖ω(t)‖,其旋转角速度为 ‖ ω ‖ ‖ω‖ ‖ω‖,则我们可知该点对应的线速率为:
S ˙ ( t ) = ω ( t ) × S ( t ) = ω ^ ( t ) ⋅ S ( t ) \dot S (t)=ω(t)×S(t)=\hat ω(t) \cdot S(t) S˙(t)=ω(t)×S(t)=ω^(t)⋅S(t)
以此,我们便可理解旋转与轴角速率及叉乘之间的关系1.3 实例
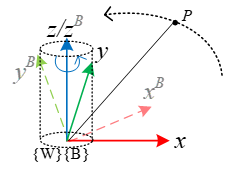
空间两个坐标系,W和B坐标系。W坐标系固定。
设B坐标系下有一点P与坐标系B固定,设其在B坐标系下坐标为: S B S_B SB(固定),其在W坐标系下坐标为: S W ( t ) S_W (t) SW(t),设:
S W ( t ) = R ( t ) ∗ S B + p ( t ) S_W (t)=R(t)*S_B+p(t) SW(t)=R(t)∗SB+p(t)
对其进行求导:
S ˙ W ( t ) = ω ^ ( t ) ⋅ R ( t ) ⋅ S B + p ˙ ( t ) = ω ^ ( t ) ⋅ ( S W ( t ) − p ( t ) ) + p ˙ ( t ) \dot S_W(t)=\hat ω(t)\cdot R(t)\cdot S_B+\dot p(t)=\hat ω(t)\cdot (S_W(t)-p(t))+\dot p(t) S˙W(t)=ω^(t)⋅R(t)⋅SB+p˙(t)=ω^(t)⋅(SW(t)−p(t))+p˙(t) = ω ^ ( t ) ⋅ S W ( t ) − ω ^ ( t ) ⋅ p ( t ) + p ˙ ( t ) =\hat ω(t)\cdot S_W(t)-\hat ω(t)\cdot p(t)+\dot p(t) =ω^(t)⋅SW(t)−ω^(t)⋅p(t)+p˙(t)
从上式可以看出,ω ω ω对应B坐标系在W坐标系下的旋转角速度, ω × S W ( t ) ω×S_W (t) ω×SW(t)即为由旋转引起的P点在W坐标系下的线速度。
− ω ^ ( t ) p ˙ ( t ) + p ^ ( t ) -\hat ω(t)\dot p(t)+\hat p (t) −ω^(t)p˙(t)+p^(t)对应点P的线速度
注意: ω ω ω为W坐标系下的向量表示。可进一步写成:
S ˙ W ( t ) = ω ^ ( t ) ⋅ S W ( t ) + v ( t ) \dot S_W (t)=\hatω(t)\cdot S_W(t)+v(t) S˙W(t)=ω^(t)⋅SW(t)+v(t)
本实例:B坐标系起始与W重合,t时刻B坐标系以 ω ( t ) = [ 0 , 0 , ω ( t ) ] ω(t)=[0,0,ω(t)] ω(t)=[0,0,ω(t)]角速度进行旋转,即B坐标系绕z轴,以 ω ( t ) ω(t) ω(t)为角速度进行旋转。
设B坐标系的旋转角为 θ ( t ) θ(t) θ(t),即 θ ˙ ( t ) = ω ( t ) \dot θ(t)=ω(t) θ˙(t)=ω(t)
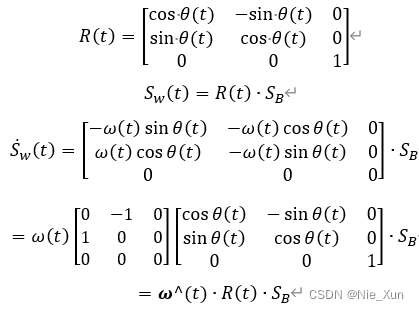
ω ˆ \omega \^{} ωˆ 在本文中与 ω ^ \hat \omega ω^同义
通过此实例,我们可以看出 ω ( t ) ω(t) ω(t)对应的旋转物理意义。
进一步我们了解到 ω ( t ) ω(t) ω(t)与则是角轴表示的角速度,从而了解角轴的叉乘几何特性。
1.4 角轴与反对称矩阵
每个轴的旋转均对应一个反对称矩阵,即将旋转同时分布在各个轴上,设如下一组:
G x = [ 0 0 0 0 0 − 1 0 1 0 ] , G y = [ 0 0 1 0 0 0 − 1 0 0 ] G z = [ 0 − 1 0 1 0 0 0 0 0 ] G_x =\left[\right], G_y =\left[0 0 0 0 0 − 1 0 1 0 \right] G_z =\left[0 0 1 0 0 0 − 1 0 0 \right] Gx= 0000010−10 ,Gy= 00−1000100 Gz= 010−100000 0 − 1 0 1 0 0 0 0 0 设角轴: θ = [ θ x , θ y , θ z ] T θ=[θ_x,θ_y,θ_z]^T θ=[θx,θy,θz]T
R = θ x G x + θ y G y + θ z G z R=θ_x G_x+θ_y G_y+θ_z G_z R=θxGx+θyGy+θzGzTips:
由此我们可以知道,角轴与欧拉角之间的小联系,当前两个旋转轴的旋转角度较小时,欧拉角 ≈ ≈ ≈轴角。2 SO3 与so3
2.1 so3 2 SO3
在我们知道: R ˙ = ω ^ R \dot R=\hatωR R˙=ω^R,便可知R可表达成e指数的形式:
R ( t ) = e x p ( [ ∫ ω ( t ) ] ˆ ) = e x p ( θ ^ ( t ) ) R(t)=exp([∫ω(t)]\^{})=exp(\hat θ(t)) R(t)=exp([∫ω(t)]ˆ)=exp(θ^(t))
即我们设计使得 R R R与角轴 θ θ θ对应。可知,由于三角函数的周期性,因此旋转矩阵到角轴是一对多的映射。由此可知,旋转矩阵对应李群SO3,而角轴表示对应李代数,其向量方向与旋转矩阵的切方向一致。
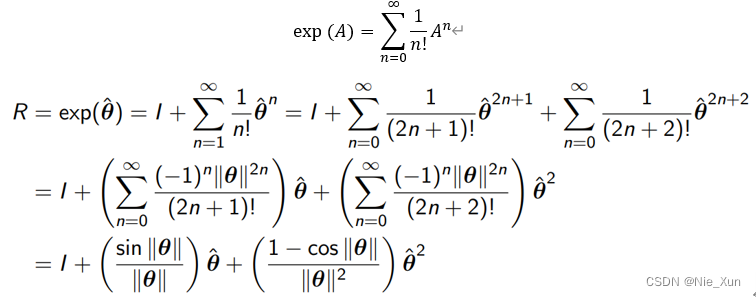
2.2 SO3 2 so3
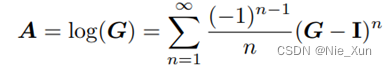
一对多的解算,其可以简化为旋转矩阵到角轴的计算:
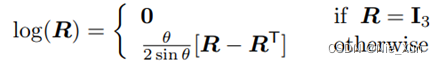
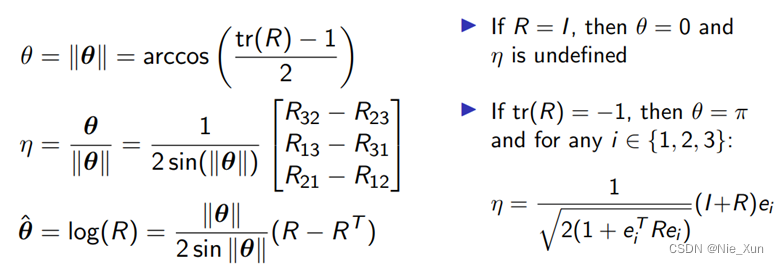
3 SE3 与se3
设SE3的变换矩阵 T T T
T ( t ) = [ R ( t ) p ( t ) 0 1 ] T(t) =\left[\right] T(t)=[R(t)0p(t)1]R ( t ) p ( t ) 0 1 同样,我们构造 T ˙ = A T \dot T=AT T˙=AT的形式,从而使得 T = e x p ( A ) T=exp(A) T=exp(A)成立。
T ˙ ( t ) = [ R ˙ ( t ) p ˙ ( t ) 0 1 ] = [ ω ^ ( t ) R ( t ) p ˙ ( t ) 0 1 ] \dot T(t) =\left[\right] =\left[R ˙ ( t ) p ˙ ( t ) 0 1 \right] T˙(t)=[R˙(t)0p˙(t)1]=[ω^(t)R(t)0p˙(t)1]ω ^ ( t ) R ( t ) p ˙ ( t ) 0 1 T ˙ ( t ) T − 1 ( t ) = [ ω ^ ( t ) − ω ^ ( t ) ⋅ p ( t ) + p ˙ ( t ) 0 0 ] = A 4 ∗ 4 \dot T(t) T^{-1} (t) =\left[
\right]=A_{4*4} T˙(t)T−1(t)=[ω^(t)0−ω^(t)⋅p(t)+p˙(t)0]=A4∗4ω ^ ( t ) − ω ^ ( t ) ⋅ p ( t ) + p ˙ ( t ) 0 0
对比1.3节的公式:
S ˙ W ( t ) = ω ^ ( t ) ⋅ S W ( t ) − ω ^ ( t ) ⋅ p ( t ) + p ˙ ( t ) = ω ^ ( t ) ⋅ S W ( t ) + v ( t ) \dot S_W (t)=\hat ω(t) \cdot S_W(t)-\hat ω(t)\cdot p(t)+\dot p(t)=\hat ω(t)\cdot S_W (t)+v(t) S˙W(t)=ω^(t)⋅SW(t)−ω^(t)⋅p(t)+p˙(t)=ω^(t)⋅SW(t)+v(t)佐证:
ω ω ω对应B坐标系在W坐标系下的旋转角速度。
v ( t ) v(t) v(t)对应W坐标系下线速度。3.1 se3 2 SE3:
se3 对应的 A A A阵为4*4的矩阵,加入偏移数据后,不再是一个反对称矩阵。我们设T阵对应的李代数为 ξ ξ ξ,其对应的李代数矩阵[ξ]表示为:
A = [ ξ ] = [ θ ^ ρ 0 0 ] A=[ξ]=\left[\right] A=[ξ]=[θ^0ρ0]θ ^ ρ 0 0 同样求e指数:
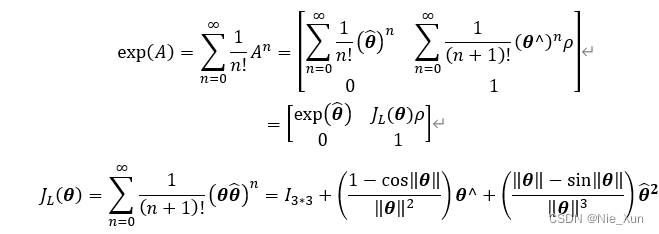
3.2 SE3 2 se3
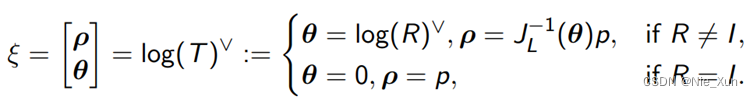
此外,注意:不成立
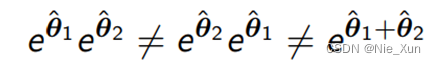
一个常用性质:
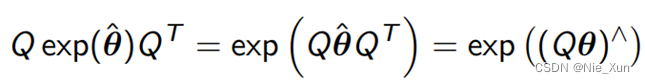
https://natanaso.github.io/ece276a2019/ref/ECE276A_12_SE3.pdf
https://vnav.mit.edu/material/04-05-LieGroups-notes.pdf4 SIM3 与sim3
SIM3与sim3之间的exp指数映射方式有多种:
- 第一种:
https://qiita.com/shinsumicco/items/a2a00a3942caf2c88ecb
[Trajectory Alignment and Evaluation in SLAM: Horn’s Method vs Alignment on the Manifold]
设一个sim3, δ δ δ,其对应的 A A A阵
A = [ δ ] = [ θ ^ + σ I 3 ∗ 3 ρ 0 3 T 0 ] A=[δ]=\left[\right] A=[δ]=[θ^+σI3∗303Tρ0]θ ^ + σ I 3 ∗ 3 ρ 0 3 T 0
e x p ( A ) = e x p ( [ δ ] ) = [ e x p ( σ ) e x p ( θ ^ ) W ρ 0 1 ] exp(A)=exp([δ])=\left[\right] exp(A)=exp([δ])=[exp(σ)exp(θ^)0Wρ1]e x p ( σ ) e x p ( θ ^ ) W ρ 0 1
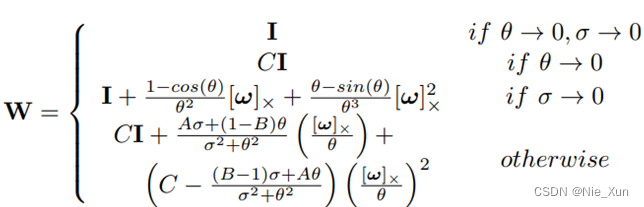
- 第二种:
https://ethaneade.com/latex2html/lie/node29.html
δ δ δ对应的A阵 A = [ δ ] = [ θ ^ ρ 0 − σ ] A=[δ]=\left[\right] A=[δ]=[θ^0ρ−σ]θ ^ ρ 0 − σ
e x p ( A ) = e x p ( [ δ ] ) = [ e x p ( θ ^ ) W ρ 0 e x p ( − σ ) ) ] exp(A)=exp([δ])=\left[
\right] exp(A)=exp([δ])=[exp(θ^)0Wρexp(−σ))]e x p ( θ ^ ) W ρ 0 e x p ( − σ ) )
具体W不给出,请与链接中查看5 Adjoint Map
https://dellaert.github.io/20S-8803MM/Readings/3D-Adjoints-note.pdf
根据上文:
S ˙ w ( t ) = ω ^ ( t ) ⋅ S W ( t ) + v ( t ) \dot S_w (t)=\hatω(t)\cdot S_W(t)+v(t) S˙w(t)=ω^(t)⋅SW(t)+v(t)
写成齐次形式:
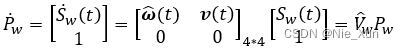
其中,
V w = [ ω ( t ) v ( t ) ] 6 ∗ 1 V_w=\left[\right]_{6*1} Vw=[ω(t)v(t)]6∗1ω ( t ) v ( t )
根据 S W ( t ) = R ( t ) ⋅ S B + p ( t ) S_W(t)=R(t)\cdot S_B+p(t) SW(t)=R(t)⋅SB+p(t)计算 P ˙ B \dot P_B P˙B与 P B P_B PB之间的映射
齐次:
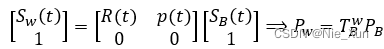
代入 P ˙ W = V W P W \dot P_W=V_W P_W P˙W=VWPW得:
T B W P ˙ B = V W T B W P B ⟹ P ˙ B = ( T B W ) − 1 V ^ W T B W P B T_B^W \dot P_B=V_W T_B^W P_B⟹\dot P_B=(T_B^W)^{-1} \hat V_W T_B^W P_B TBWP˙B=VWTBWPB⟹P˙B=(TBW)−1V^WTBWPB
从而可知:
V ^ B = ( T B W ) − 1 V ^ W T B W = T W B V ^ W ( T W B ) − 1 \hat V_B=(T_B^W )^{-1} \hat V_W T_B^W=T_W^B \hat V_W(T_W^B )^{-1} V^B=(TBW)−1V^WTBW=TWBV^W(TWB)−1
以上便是Adjoint Map,可见Adjoint Map是将速度之间的映射
我们可以从 V ˙ B \dot V_B V˙B与 V ˙ W \dot V_W V˙W之间的关系中,找到 V W V_W VW与 V B V_B VB之间的映射。 V W V_W VW与 V B V_B VB为6维向量,而 V ^ B \hat V_B V^B与 V ^ W \hat V_W V^W为4*4的向量构成的方阵。
令:
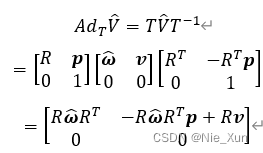
根据叉乘的反交换律和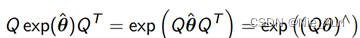
可得:
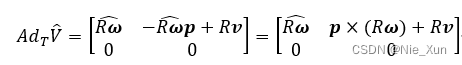
从而根据:
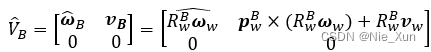
可得:
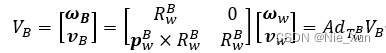
- 第一种:
-
相关阅读:
“终于懂了” 系列:组件化框架 ARouter 完全解析(二)APT技术
【Linux】IO操作
Selenium WebUI 自动化测试框架
ubuntu下C++调用matplotlibcpp进行画图(超详细)
Docker实践经验:Docker 上部署 mysql8 主从复制
【Python】解析CPP类定义代码,获取UML类图信息
Day22 SSH远程管理服务
曼哈顿距离
卷积神经网络识别眼睛转向
【LeetCode每日一题:792.匹配子序列的单词数~~~时间超限的双指针+改进优化的存储元素位置的二分查找】
- 原文地址:https://blog.csdn.net/weixin_41469272/article/details/134532459