-
MATLAB | 官方举办的动图绘制大赛 | 第二周赛情回顾
今天带来一下MATHWORKS官方举办的迷你黑客大赛第三期(MATLAB Flipbook Mini Hack)的最新进展!!目前比赛已经进行了两周非常荣幸能够成为第一周的阶段性获奖者:

本来并不打算每周进行一次赛况讲解,但是由于字符限制改成了2000,大家的创造力仿佛上了一个台阶,一周内又是超级多优秀的作品被给出,
本次比赛要求提交名为
drawframe(f)的函数代码,生成长达2s,48帧的动态图,动图生成是依靠如下代码来做到的:function contestAnimator() animFilename = 'animation.gif'; % Output file name firstFrame = true; framesPerSecond = 24; delayTime = 1/framesPerSecond; % Create the gif for frame = 1:48 drawframe(frame) fig = gcf(); fig.Units = 'pixels'; fig.Position(3:4) = [300,300]; im = getframe(fig); [A,map] = rgb2ind(im.cdata,256); if firstFrame firstFrame = false; imwrite(A,map,animFilename, LoopCount=Inf, DelayTime=delayTime); else imwrite(A,map,animFilename, WriteMode="append", DelayTime=delayTime); end end end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
闲话少叙,一起看作品!!
作品概览
Tim大佬继续大展身手:Tim / Lanterns
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/14082

function drawframe(f) tic persistent frms % Once again, doing all the primary plotting at f==1 and just % Storing the frame data rng default if f==1 NL=200; % Number of lanterns xyzL=rand(3,NL).*[6;6;3]*10+[0;0;2]*1; % Locations % Create lanterns & interiors and store handles for n = 1:NL [xc,yc,zc,cmp]=lantern(.6+.4*rand(1),(rand(1)-.5)*.1); r=sqrt(xc(1).^2+yc(1).^2); [xl,yl,zl]=ll(r,zc(1)); S{n}=warp(xc+xyzL(1,n),yc+xyzL(2,n),zc+xyzL(3,n),cmp); hold on; S2{n}=warp(xl+xyzL(1,n),yl+xyzL(2,n),zl+xyzL(3,n),cmp(1:10,1,:).^.5); C1{n}=S{n}.CData; C2{n}=S2{n}.CData; end % Twinkler lgt=exp(-linspace(-1,1,49).^2*200)'*ones(1,NL); for n=1:NL lgt(:,n)=1-circshift(lgt(:,n),randi(48,1))*rand(1)*.7; end % This lantern will be the focus of the scene sl=[5,5,3]; [xc,yc,zc,cmp]=lantern(.6+.4*rand(1),(rand(1)-.5)*.1); r=sqrt(xc(1).^2+yc(1).^2); [xl,yl,zl]=ll(r,zc(1)); warp(xc+sl(1),yc+sl(2),zc+sl(3),cmp); warp(xl+sl(1),yl+sl(2),zl+sl(3),cmp(1:10,1,:).^.6); % Create motion vector for each lantern rand(6,NL); % Jogging the random stream to a position I like xm=randn(3,NL).*[1;.5;1]/40; % Make figure big to reduce aliasing S{1}.Parent.Parent.Position(3:4)=[1120,840]; % Pretty axis equal off set(gcf,'color',[.2,.1,.15]); camproj p camva(40); camtarget(sl); % Loop poses for n = 1:48 % Update lantern positions & twinkle for m = 1:NL S{m}.XData=S{m}.XData+xm(1,m); S2{m}.XData=S2{m}.XData+xm(1,m); S{m}.YData=S{m}.YData+xm(2,m); S2{m}.YData=S2{m}.YData+xm(2,m); S{m}.ZData=S{m}.ZData+xm(3,m); S2{m}.ZData=S2{m}.ZData+xm(3,m); S{m}.CData=C1{m}.*lgt(n,m); S2{m}.CData=C2{m}.*lgt(n,m); end % Update camera position campos([n/(17),n/100,n/80]); % Get frame, apply anti-alias filter and decimate R=getframe(gcf); R=imgaussfilt(double(R.cdata)/255,2); frms{n}=R(1:2:end,1:2:end,:); end close end % Load frame IG=frms{f}; % Apply glow for n = 1:2 IG=max(IG,imgaussfilt(IG,21)); end % Final frame: image(IG); axis equal off camva(5) toc end % Lantern interior: a lit hemisphere function [x,y,z]=ll(r,zo) [x,y,z]=sphere(20); x=x(11:end,:)*r; y=y(11:end,:)*r; z=z(11:end,:)+zo; end % Lantern exterior % f (randomized when called) controls shape % s (randomized when called) controls hue function [x,y,z,cmp]=lantern(f,s) wn=tukeywin(30,f); [xc,yc,zc]=cylinder(wn,20); xc=xc(9:end,:); yc=yc(9:end,:); zc=zc(9:end,:); zc=zc-.5; x=xc.*(rescale(zc)+2)/3; y=yc.*(rescale(zc)+2)/3; z=erf(zc*4)*1.5; z=z*max((min(1-f,.3)/.3),.5); % Special colormap for lanterns y1=[245,241,130]/255; y2=[255,142,76]/255; y3=[203,121,71]/255; cmp=interp1([1,80,256]',[y1;y2;y3*.5],(1:256)','spline'); % Rotate hue of colormap g=rgb2hsv(min(cmp,1)); g(:,1)=g(:,1)+s; g(g<0)=1+g(g<0); cmp=hsv2rgb(g); cmp=permute(cmp,[1,3,2]); %S.D.G. end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
Tim / Morning ascent
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/13820

function drawframe(f) % Trying to meet last years character limits! if f == 1 rng(1,'v4') x=(-1:.005:1).^2; g=30*abs(ifft2(exp(6*i*rand(401))./(x'+x+1e-5))); s=@(x,y)surf(x,'EdgeC','none','FaceC',y); s(g,'k'); hold s(conv2(g+1,ones(20)/400),'w'); axis equal off camproj p; camva(40); end campos([20 20+f 45+f/2]); set(gcf,'color',[0,.1,.3]+f/69); light('color',[2,1,1]/4); en- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
Tim / Ruby
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/13952

function drawframe(f) % Red version / bigger scales. persistent frms % All we will be keeping is the cell array of frames because % the whole loop will run on the first function call. % The reason for this is that some spatially variant % blurring will be applied to the RGB data on each % loop. tic if f == 1 % Base texture scale x=linspace(-4, 4, 400); % Shape of scale - ovalish but extended on one side m=1-(erf(50*(3*x'.^2+x.^2-.5)+max(24*x.^5,-20))+1)/2; % Basic scale shape & mask m=max(m,circshift(m,[0,5])); % Needs to be a bit longer % Scales are slightly curved s=m.*cos(2*x'); s=s-x.*m/3; % Needs change in height so that it overlaps well k=m.*rescale(1./(abs(x') + 0.01))*0.1.*(min(0,x-0.3).^2); % Add keel s=s+k+conv2(m.*randn(size(k))/100, ones(1,11)/11, 'same'); % Some textury-noise % Now the tiling... so=s; SS=40; for n = 1:9 so = max(so, circshift(s, n*SS)); end so = max(so, circshift(so, [SS/2, 40])); for n = 1:4; so = max(so, circshift(so, [0, 80*n])); end so(so<0.7)=0.7; % Turn into radial distance so=so*0.4; so=so'+10; so=flipud(so); % More tiling so=[so,so]; so=[so;so]; % Apply to snake body. Snakes are not cylindrical, they have a prominent % spine and flat underside (sort of / lots of variation here) a=linspace(0,2*pi,size(so, 2))-pi; sob=so; so = so + (exp(-(a).^2*50) - exp(-(a+pi).^2*2)*2)- exp(-(a-pi).^2*2)*2; x=sin(a).*so; y=cos(a).*so; z=linspace(-1,1,size(x,1))'.*ones(1,length(a))*8*3; % Woops, that was too high resolution. Cut off the backside so it renders x=x(:, (1:325)+375); y=y(:, (1:325)+375); z=z(:, (1:325)+375); sob=sob(:, (1:325)+375); % Still too high resolution. Decimate... % x=x(1:2:end, 1:2:end); % y=y(1:2:end, 1:2:end); % z=z(1:2:end, 1:2:end); % sob=sob(1:2:end, 1:2:end); % Plot S=surf(x,z,y,rescale(sob).*cat(3,1,.2,0), 'SpecularStrength', 0.5, 'DiffuseStrength', 1, 'AmbientStrength', 0); shading flat % Too pixelated. Make larger S.Parent.Parent.Position(3:4)=[1120,840]; % Camera setup etc. axis equal off set(gcf, 'color', 'k'); light('position', [0, 0, 1]); view([90, 10]); camtarget([0,-4,5]); campos([265, 0.05*n*4, 48]); camproj p camva(5); % Rotate snake through image in 48 frames for n = 1:48 S.YData = z -.05*n*4; S.ZData = y - .004*(S.YData+4).^2; drawnow; frms{n}=getframe(gcf); end % Close because we are actually going to work with the rgb data close end % Now lens blur simulation -> weight w/cosine tapering wn=min((1-cos(linspace(0, 2*pi, size(frms{f}.cdata(:,:,1),2))))/1.9, 1); IG=flt(frms{f}.cdata,wn,2); % Decimate IG=IG(1:2:end, 1:2:end, :); image(IG); axis equal off camva(6) toc end % Local smoother function in=flt(in,wgt,nits) if nargin == 1 wgt = zeros(size(in(:,:,1))); nits=1; end in = double(in)/255; % Blur kernel krn = [1, 2, 3, 4, 5, 4, 3, 2, 1]'; krn = krn*krn'; krn = krn/sum(krn(:)); % Apply to each color channel for m = 1:3 for mm = 1:nits in(:, :,m) = wgt.*in(:,:,m) + (1-wgt).*conv2(in(:,:,m), krn, 'same'); end end % S.D.G. end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
Tim / Fracture
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/14377

function drawframe(f) % Done with my kids! Explosion using voronoi cells. persistent V T T2 Vg Xo R C L L2 rng default N=150; % Number of voronoi domains v=@(x)vecnorm(x); % This is used a lot... if f==1 % Distribute points in the unit sphere, biased toward the center Xo=randn(3,N); Xo=Xo./v(Xo).*rand(1, N); % Bounding layer of points that will create our outer surface. Need % lots of them... NA=100; ps=randn(3,NA); ps=1.3*ps./v(ps); % Concatenate X=[Xo,ps]'; % Voronoi diagram [V,R]=voronoin(X); mnR=cellfun(@min, R)~=1; % Which cells have inf's ginds=unique(cell2mat(R(~mnR)')); % Get bordering nodes Iinds=setdiff(1:size(V,1), ginds); % Get interior nodes mxr=max(v(V(Iinds,:)')); ginds(1)=[]; % Get rid of inf % Make non-inf outer-nodes have unit radius * some small scale factor V(ginds,:)=1.3*V(ginds,:)./v(V(ginds,:)')'; % Glow Vg=ones(size(V,1),1); Vg(ginds)=0; TS=@(k,x,y,z,C)trisurf(k,x,y,z,'FaceC',C,'EdgeC','none'); cnt = 1; for n = 1:length(mnR) if mnR(n) == 1 xt=V(R{n},1); yt=V(R{n},2); zt=V(R{n},3); C=[1,1,1]; k = convhull(xt,yt,zt); T{n}=TS(k,xt,yt,zt,C/2); hold on; material(T{n},[0,1,0,3]); s=1.1; T2{n}=TS(k,xt*s,yt*s,zt*s,C); material(T2{n},[1,0,0,3]); set(T2{n},'FaceAlpha','interp','FaceVertexAlphaData',.1*Vg(R{n}),'AlphaDataMapping','None'); if cnt == 1 set(gca, 'color', 'k'); axis equal off axis([-1,1,-1,1,-1,1]*6); cnt = cnt + 1; camproj p camva(70); campos([-55-5 -71 52]/30); set(gcf,'color','k'); L2=light; L{1}=light('position',[0,0,0],'style','local'); L{2}=light('position',[0.1,0,0], 'style','local'); end end end elseif f<10 for n=1:N T2{n}.FaceVertexAlphaData = .1*Vg(R{n})*f; end L2.Color = C/f; elseif f >= 10 % Loop over fragments and expand for n = 1:N T2{n}.Vertices=1.3*V(R{n},:)*4000/f.^3; T2{n}.FaceVertexAlphaData=T2{n}.FaceVertexAlphaData*.95; T{n}.Vertices=T{n}.Vertices+2.5*Xo(:,n)'/f; end if f > 20 for n=1:2 L{n}.Color=L{n}.Color*.96; end L2.Color = C*f/48; end end end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
Jr大佬的一系列字符够成的画:Jr / the rise of Matzilla!
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/14292

%Hello all!! %I started this code with one of my 2021 mini hack images: %https://www.mathworks.com/matlabcentral/communitycontests/contests/4/entries/3626 %The result is just some layers of ocean made with two sines each, a good %"capture" of them, and an emoji of our cute monster up and down. %Aah, and some triangles to make him not so cute. %First, we make layers of blue waves, then we make MATzilla and finally, we finish adding more waves. function drawframe(f) c=1200; d=700; n=800; m=.37; hold on; %Let's make the ocean (1st part): we have some layers here [18-9] (behind Matzilla). for i=18:-1:9 y=i/11*d; a=10*m^(i-1); u=c*(1-(i-1)/8); x=linspace(0,c,n); p=y/d*4*pi; t=x*2*pi/u; q=sin(f/4+.3*t)+sin(f/8+.2*t); %if you'll remix another ocean, %you can change the frequency of them, or the amplitude... I used a frequency %division whose result is an integer to make the waves move 1 period within 2 %seconds. r=y+q*120*.8^(i-1);+3^(i-1); v=[ x' r'; c 0; 0 0]; %making the ocean blue; fill(v(:,1),v(:,2),i/18*[.1 .7 1],'EdgeColor','n'); end %Now we can use emojis to make Matzilla: Dino + triangles. %Move them with the variable "f" forward and backward. if 24>=f ht=text(380+f,670+f,'🦖','color','black','FontSize',60); ht.Rotation = -55 it=text(850+f,609+f,'▲','color','black','FontSize',20); it.Rotation = -55 jt=text(975+f,579+f,'▲','color','black','FontSize',30); jt.Rotation = -65 kt=text(1040+f,525+f,'▲','color','black','FontSize',30); kt.Rotation = -65 else ht=text(405+(25-f),695+(25-f),'🦖','color','black','FontSize',60); ht.Rotation = -55 it=text(875+(25-f),634+(25-f),'▲','color','black','FontSize',20); it.Rotation = -55 jt=text(1000+(25-f),604+(25-f),'▲','color','black','FontSize',30); jt.Rotation = -65 kt=text(1065+(25-f),550+(25-f),'▲','color','black','FontSize',30); kt.Rotation = -65 end %Ocean (2 part): we have more layers here [9-7] (in front of Matzilla). for i=9:-1:7 y=i/11*d; a=10*m^(i-1); u=c*(1-(i-1)/8); x=linspace(0,c,n); p=y/d*4*pi; t=x*2*pi/u; q=sin(f/4+.3*t)+sin(f/8+.2*t); r=y+q*120*.8^(i-1);+3^(i-1); v=[ x' r'; c 0; 0 0]; fill(v(:,1),v(:,2),i/18*[.1 .7 1],'EdgeColor','n'); end %final adjustments for plotting. Hope you like it. ;) axis off; ylim([250,n]) end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
Jr大佬的一系列字符够成的画:Jr / NOOO!!! Matzilla hit us!!
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/14302

%well, I made this just by changing (again) my previous code. The %process is the same: % 1. We make layers of the blue sky; % 2. We add emojis up and down (it's funny to control the movement of them) % 3. We make layers of green mountains; function drawframe(f) c=1200; d=700; n=800; m=.37; hold on; %Making the sky: for i=15:-1:13 y=i/11*d; a=20*m^(i-1); u=c*(1-(i-1)/8); x=linspace(0,c,n); p=y/d*4*pi; t=x*2*pi/u; q=sin(f/4+.3*t)+sin(f/8+.2*t); r=y+q+cumsum(sqrt(a)*randn(1,n));+3.2^(i-1); v=[ x' r'; c 0; 0 0]; fill(v(:,1),v(:,2),i/18*[.7 .7 .7],'EdgeColor','n'); end %Using emojis and moving them with our parameter "f" as well: ht=text(380-(f*5),670-(f*5),'🛩','color','black','FontSize',40); if f>=38 ht=text(50,500,'🔥','color','r','FontSize',80); end hc=text(10+f*2,660,'☁','color','w','FontSize',20); ic=text(450+f*4,780,'☁','color','w','FontSize',30); kc=text(850+f*3.5,610,'☁','color','w','FontSize',50); %Making the mountains for i=9:-1:4 y=i/11*d; a=170*m^(i-1); u=c*(1-(i-1)/8); x=linspace(0,c,n); p=y/d*4*pi; t=x*2*pi/u; q=sin(f/2+.3*t)+sin(f/8+.2*t); r=y+q+cumsum(sqrt(a)*randn(1,n));+3.2^(i-1); %unlike the previous code, %here there is a random/noisy component to make it look like grass/earth v=[ x' r'; c 0; 0 0]; fill(v(:,1),v(:,2),i/18*[216 171 100]/255,'EdgeColor','n'); end %final adjustments for plotting. axis off; ylim([200,n]) end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
以下就直接放代码不咋说明啦:
Adam Danz / Rainy window
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/14367

function drawframe(f) persistent T dropSzFcn dropFcn if f==1 || isempty(T) rng(359,'twister') % set the random number generator for reproducibility nc=50; % number of colors in colormap cmap=gray(nc); % used to set the background color axes(Position=[0 0 1 1]) % example axes to full size of figure colormap(cmap(1:ceil(0.4*nc),:)) % cut out the upper (lighter) part of the colormap hold on % background image bx=1:50; % set size of the square image by=exp(-(((bx-6).^2)/(2*8.^2))); % gaussian I=imagesc([0,1],[0,1],by'+0*bx); axis tight equal off % add distant lights ncl=99; % number of colors for the lights LC=hot(ncl); % light colors nl=30; % number of lights r=@()rand(nl,1); % generate nlx1 random numbers 0:1 b=bubblechart(r(),r(),r(),LC(randi(ncl,nl,1),:),MarkerEdgeColor='n'); % street lights figSz=get(gcf,'Pos'); bubblesize([3,0.1*max(figSz(3:4))]) % Scale light size to figure size % blur the image % the background and lights are flattened into a single image and % blurred. f=getframe; b.delete I.CData=imfilter(flipud(f.cdata),ones(10)/100); % Add rain drops nd=99; % number of drops T=table(); % use a table to store some variables T.obj=gobjects(nd,1); % droplet surf objects T.dropSz=nan(nd,1); % scale factor for drop size dropSzFcn=@()max(min(randg(1),6),.8)/150; % Drop size, truncated gamma distribution [x,y,z]=sphere(20); % use a larger number for smoother raindrop surfaces, but slower. dropFcn=@(sz)surf(sz*x+rand,2*sz*y+rand*1.1,sz*max(z,0),... % function to create raindrops FaceCo='w',FaceAl=.2,EdgeCo='n',... SpecularSt=1,SpecularExp=2, ... DiffuseSt=1,AmbientSt=.1); for i=1:nd % Create the rain drops T.dropSz(i)=dropSzFcn(); T.obj(i)=dropFcn(T.dropSz(i)); end light(Po=[0.5 -1 0.1]); % rain drops should be dark on top and light on bottom xlim([0,1]) ylim([0,1]) set(gcf,Color='k') end % Add new drops n=5; % number of rain drops to add T2=table(); % create a temporary table to store variables T2.obj=gobjects(n,1); % droplet surf objects T2.dropSz=nan(n,1); % scale factor for drop size for k=1:n % add more raindrops T2.dropSz(k)=dropSzFcn(); T2.obj(k)=dropFcn(T2.dropSz(k)); end T=[T;T2]; % Determine which rain drops are falling by drop size (larger ones fall) % figure(); histogram(T.dropSz) % for decision making T.isFalling=T.dropSz > 0.01; % Reduce threshold to increase the number of falling rain drops % The amount of downward displacement is determined by drop size for j=find(T.isFalling') T.obj(j).YData=T.obj(j).YData-T.dropSz(j); % shift downward end % Determine if any drops overlap % Reduce the computational expense by assuming drops are rectangular and % useing MATLAB's rectint, though it contains 1 extra step that isn't needed % (computing area of overlap) but it's still fast and clean. [mmy(:,1),mmy(:,2)]=arrayfun(@(h)bounds(h.YData,'all'),T.obj); % [min,max] for ydata [mmx(:,1),mmx(:,2)]=arrayfun(@(h)bounds(h.XData,'all'),T.obj); % [min,max] for xdata % Covert the drop's x and y data to rectangular vectors [x,y,width,height] T.xywh=[mmx(:,1),mmy(:,1),diff(mmx,1,2),diff(mmy,1,2)]; % If a water drop is off the figure, remove it T.isoff=mmy(:,2) < 0; T.obj(T.isoff).delete; T(T.isoff,:)=[]; % Compare all pairs of drops without duplicate comparisons objPairs=nchoosek(1:height(T),2); overlap=false(height(objPairs),1); for q=1:height(objPairs) % Because we're treating the raindrops as rectangles, there will be % falsely labeled overlaps in the corner of the rectangles. To reduce % the number of false positives, we'll require the overlap to be at least % 21.5% of the smallest raindrop since a circle consumes 78.5% of its % bounding box. minArea=min(prod(T.xywh(objPairs(q,:),[3,4]),2))*(1-.785); overlap(q)=rectint(T.xywh(objPairs(q,1),:),T.xywh(objPairs(q,2),:)) > minArea; if overlap(q) && all(isvalid(T.obj(objPairs(q,:)))) % highlight the overlapping raindrops, for troubleshooting % set(T.obj(objPairs(q,:)),'facecolor','m','AmbientStrength',1 ) % Which drop has the smallest width? [~,minidx]=min(T.xywh(objPairs(q,:),3)); % The smaller drop is absorbed (removed) T.obj(objPairs(q,minidx),:).delete; % Elongate the surviving droplet maxidx=abs(3*(minidx-1)-2); % converts 2 to 1 or 1 to 2; yd=T.obj(objPairs(q,maxidx)).YData; ydmu=mean(yd,'all'); ef=1.05; % elongation factor T.obj(objPairs(q,maxidx)).YData=(ef*(yd-ydmu))+ydmu; % Update dropSz T.dropSz(objPairs(q,maxidx))=ef*T.dropSz(objPairs(q,maxidx)); % Make the elongaged drops narrower xd=T.obj(objPairs(q,maxidx)).XData; xdmu=mean(xd,'all'); T.obj(objPairs(q,maxidx)).XData=(1/ef*(xd-xdmu))+xdmu; end end % Remove rows of the table that belong to deleted rain drops T(:,3:end)=[]; % Remove the columns that will be recomputed on next iteration T(~isvalid(T.obj),:)=[]; end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
Eric Ludlam / Lonely Lighthouse
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/14022

function drawframe(f) % shortenners r=@rand; ls=@linspace; % Make all our circles the same nv=300; th=ls(0,2,nv); X=cospi(th); Y=sinpi(th); Z=ones(1,nv); % Stuff in front needs to be pushed ahead of the backdrop images FZ=2; if f==1 set(gca,'position',[0 0 1 1],'clipping','off'); hold on imagesc([-1 1],[1.5 0],(1:256)'); colormap(abyss.^2) % square to get more black, but it made the blue niftier too %% Starry sky % do first due to newplot N=120; si=r(1,N); % Size and Color are related, so use same random #s scatter(r(1,N)*2-1,r(1,N)*1.3+.1,(si+.2)*40,(si*.5+.5)'.*[1 1 1],'Marker','.'); %% Lighthouse lh_r=[.16 .1 .15 .15 .05 .05 .14 0]'*.5; lh_y=[.1 .78 .78 .82 .82 .89 .89 1]'; lh_c=[.5 .5 .3 .3 1 1 .3 .3]'; % shade of gray means I only need 1 # per profile ring HC=ones(1,nv,3).*lh_c; % convert lh_c to RGB color surface(X.*lh_r,Z.*lh_y,Y.*lh_r+FZ,HC,'FaceC','f','EdgeC','n'); % Make the light part brighter by setting FaceLighting to none lhlr=[.1 .1]'*.5; surface(X.*lhlr,Z.*[.8 .9]',Y.*lhlr+FZ,'FaceC','w','EdgeC','n','FaceL','n'); %% The lighthouse sits on a rock N=120; RN=12; % This computes random points on a half sphere. r_th=r(1,N)*2; u=r(1,N)*2-1; rth=ls(0,2,RN+1); rth(end)=[]; pts=[0 cospi(r_th).*sqrt(1-u.^2) cospi(rth) 0 sinpi(r_th).*sqrt(1-u.^2) sinpi(rth) 0 abs(u) zeros(1,RN)]'; % Form the patch around the random pts using convex hull lf=convhulln(pts); % Move pts in/out to make it bumpy and scale into our world. % You have to make it bumpy after convex hull b/c that ignores pts 'inside' the hull. D=(.9+r(1,N+RN+1)*.3)'; lv=pts.*D.*[.5 .11 .3]; % Adjust colors to be darker in depths. I=[.55 .41 .36];% brown C=hsv2rgb(rgb2hsv(I).*[1 1 .5]); q=I-C; patch('Faces',lf,'Vertices',lv(:,[1 3 2])+[0 0 FZ],'FaceC','i', ... 'EdgeC','none','FaceVertexCData',rescale(D)*q+C,'FaceL','g'); %% The light beam (fill in later) patch('tag','LB','vertices',[],'faces',[],... 'edgec','n','facec','w','facea','i','facel','n') %% Reflection off the ocean (fill in later) image([-1 1],[-.5 .02],rand(200),'tag','O'); %% Nicify axes material([.6 .6 .8 2 .8]) axis([-1 1 -.5 1.5],'off'); daspect([1 1 1]) light('pos',[0 0 0],'color',[.5 .5 .6 ],'tag','LBO'); end % Find all our objects from initial creation LB=findobj('tag','LB'); LBO=findobj('tag','LBO'); O=findobj('tag','O'); %% Create the light-beam eminating from the lighthouse A=interp1([1 49],[0 2],f); % Angle to point light beam for this frame % Create a mask (pts) to project through. % Mask is a circle in cylindrical coords with a wavy radius (defined by wf) wf=cospi(th*50)*.003; os=X*.15+A; mx=cospi(os).*(.08+wf); my=Y*.03+.85; mz=sinpi(os).*(.07+wf); pts=[mx my mz]'; % Light posn for projection L=[0 .85 0]; % Set posn of our actual light so the tower/rock is illuminated by % the light bean reflecting off the air / virtual fog set(LBO,'Pos', [ cospi(A) L(2) sinpi(A) ]); %% Extrude a cone of light through the mask % Compute normalized vectors away from light through each vertex vv=(pts-L)./vecnorm(pts-L,2,2); % Compute length and alpha based on angle to camera. % The idea is that the more 'volume' of light you see through the more particles % in the air it reflects off. Whe light points at you, simulate by less transparency. % when pointing at the side, more transparency. % To do it right, we'd use dot product, but we can estimate in less % characters using sin instead since we're pointing flat out in Z %ctr=[mx(2) my(2) mz(2)]; % center %cp=[0 .5 10]; S=sinpi(A); %dot(ctr,dn(mean(pts,1),cp),2); ce=vv*(max(S,0)^2*2+1); % Extrude ed=mod((0:(nv-1))'+[0 1],nv)+1; R=1:nv;%size(ed,1) c1=[ed(R,[2 1 2])+[0 0 nv];% edges connecting top/bottom ed(R,[1 1 2])+[0 nv nv]]; f=[c1 c1+nv c1+nv*2]; v=[pts pts+ce*.3 pts+ce*.5 pts+ce]; av=[S .9 .7 0]; M=@(a)repmat(a,nv,1); a=[ M(av(1)) M(av(2)) M(av(3)) M(av(4)) ] * ... rescale(S,.2,.8,'inputmax',1,'inputmin',-.8)^2; set(LB,'vertices',v+[0 0 FZ],'faces',f,'facevertexalphadata',a); %% Reflect the upper half into the ocean f=getframe(gca); % Darken it by passing through hsv and lowering V % Use guass filter to blur slightly so it doesn't look so computery O.CData=hsv2rgb(rgb2hsv(imgaussfilt(f.cdata(1:end-110,:,:),1)).*reshape([1 1 .7],1,1,3)); end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
Dhimas Mahardika Sanggung Utara / A 2D Candle Equation
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/14272
function drawframe(f) h = linspace(0,100*pi,48); syms x y eqn = ((2*x^2)- (((sin(3*y^0.5))^2)/15) - 0.12*x*sin(3*y+h(f)) + y^200 +0.007)*(abs(5*x+y+1.6)+abs(5*x-y-1.6)-3)*(abs(15*x+0.75*(y-0.033))+abs(15*x-0.75*(y-0.033))-0.2) == 0; fimplicit(eqn,[-1,1,-3.3,1.2], MeshDensity=500,LineStyle="-"); axis equal end- 1
- 2
- 3
- 4
- 5
- 6
- 7
hiahiahia我写的一个超简单的小人
Zhaoxu Liu / slandarer / Math-Matchstick Man
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/14012
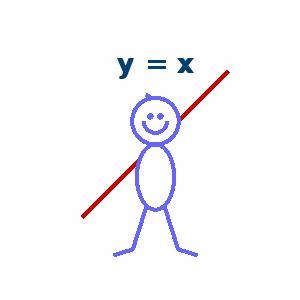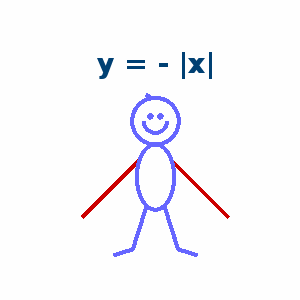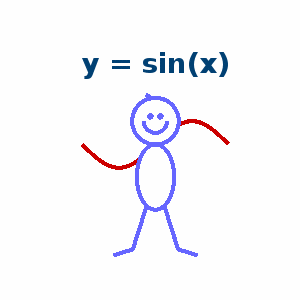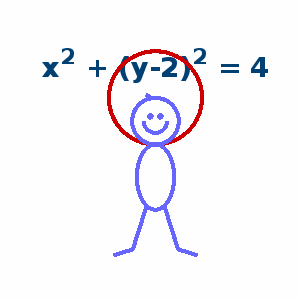
function drawframe(n) persistent txtHdl armHdl if n==1 ax=gca; ax.DataAspectRatio=[1,1,1]; ax.XLim=[-5,5]; ax.YLim=[-5,5]; ax.XColor='none'; ax.YColor='none'; hold on txtHdl = text(0,3.5,'y = x','FontSize',20,'FontName','Times New Roman','FontWeight','bold',... 'HorizontalAlignment','center','Color',[0,.25,.45]); armHdl = plot([-pi,pi],[-pi,pi],'Color',[.8,0,0],'LineWidth',3); t=linspace(0,2*pi,200); fill(cos(t),sin(t)+1,[1,1,1],'EdgeColor',[.4,.4,1],'LineWidth',3) plot(cos(t(101:200)).*.5,sin(t(101:200)).*.5+1,'Color',[.4,.4,1],'LineWidth',3) fill(cos(t).*.8,sin(t).*1.4-1.4,[1,1,1],'EdgeColor',[.4,.4,1],'LineWidth',3) plot([-0.38,-0.97,-1.81],[-2.64,-4.50,-4.76],'Color',[.4,.4,1],'LineWidth',3) plot([ 0.38, 0.97, 1.81],[-2.64,-4.50,-4.76],'Color',[.4,.4,1],'LineWidth',3) plot([-0.15,-0.42],[ 1.98, 2.15],'Color',[.4,.4,1],'LineWidth',3) scatter([-0.2,0.2],[1.2,1.2],25,[.4,.4,1],'filled','o') end switch true case n>=7 && n<=12 armHdl.XData = [-pi,0, pi]; armHdl.YData = [ pi,0, pi]; txtHdl.String = 'y = |x|'; case n>=13 && n<=18 armHdl.XData = [-pi,0, pi]; armHdl.YData = [-pi,0,-pi]; txtHdl.String = 'y = - |x|'; case n>=19 && n<=24 armHdl.XData = -2:.02:2; armHdl.YData = (-2:.02:2).^2; txtHdl.String = 'y = x^2'; case n>=25 && n<=30 armHdl.XData = -2:.02:2; armHdl.YData = (-2:.02:2).^3; txtHdl.String = 'y = x^3'; case n>=31 && n<=36 armHdl.XData = -pi:.01:pi; armHdl.YData = sin(-pi:.01:pi); txtHdl.String = 'y = sin(x)'; case n>=37 && n<=42 armHdl.XData = -2.5:.02:2.5; armHdl.YData = 2.^(-2.5:.02:2.5)-1; txtHdl.String = 'y = 2^x - 1'; case n>=43 && n<=48 t=linspace(0,2*pi,200); armHdl.XData = cos(t).*2; armHdl.YData = sin(t).*2+2; txtHdl.String = 'x^2 + (y-2)^2 = 4'; end end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
Eric Ludlam / Snake Toy
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/14042

function drawframe(f) %% Core Matrices numblock=24; v = [ -1 -1 -1 ; 1 -1 -1 ; -1 1 -1 ; -1 1 1 ; -1 -1 1 ; 1 -1 1 ]; pf = [ 1 2 3 nan; 5 6 4 nan; 1 2 6 5; 1 5 4 3; 3 4 6 2 ]; clr = hsv(numblock); % Left in a few options for anyone interested in remixing other shapes % and colors %n = pi/2; shapes = [ 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 % box %0 0 .5 -.5 .5 0 1 0 -.5 .5 -.5 0 1 0 .5 -.5 .5 0 1 0 -.5 .5 -.5 0 % fluer %0 0 1 1 0 .5 -.5 1 .5 .5 -.5 -.5 1 .5 .5 -.5 -.5 1 .5 .5 -.5 -.5 1 .5 % bowl %0 1 0 0 0 1 1 0 1 0 0 1 0 1 1 0 0 0 1 0 1 1 0 1 % dog %0 1 0 0 0 0 0 1 1 0 .5 0 1 1 0 1 1 0 -.5 0 1 1 0 0 % chicken %0 1 0 0 0 1 1 0 0 0 0 1 0 0 1 0 0 0 0 1 1 0 0 0 % filled box %0 1 -n 0 0 0 1 n n 0 1 0 0 0 n 0 1 1 0 1 1 0 n 0 % cobra 0 .5 -.5 -.5 .5 -.5 .5 .5 -.5 .5 -.5 -.5 .5 -.5 .5 .5 -.5 .5 -.5 -.5 .5 -.5 .5 .5]; % ball % Helper for making transform matrices. xform=@(R)makehgtform('axisrotate',[0 1 0],R,'zrotate',pi/2,'yrotate',pi,'translate',[2 0 0]); if f==1 %% Create a neon type snake toy on a black background set(gcf,'color','black'); axes('position',[0 0 1 1],'visible','off') P=hgtransform('Parent',gca,'Matrix',makehgtform('xrotate',pi*.5,'zrotate',pi*-.8)); for i = 1:numblock P = hgtransform('Parent',P,'Matrix',xform(shapes(end,i)*pi)); patch('Parent',P, 'Vertices', v, 'Faces', pf, 'FaceColor',clr(i,:),'EdgeColor','none'); patch('Parent',P, 'Vertices', v*.75, 'Faces', pf(end,:), 'FaceColor','none',... 'EdgeColor','w','LineWidth',2); end %% Axes setup daspect([1 1 1]); view([10 60]); axis tight vis3d off camlight end % Get our stack of transforms. These will magically be in the right order. h=findobj('type','hgtransform')'; h=h(2:end); % Skip the first one % Orbit once around view([-f*360/48 20]); % Script Steps (transform there and back again) if f<=5 return elseif f<=41 steps=35; r=shapes(end,:)*pi; % Start at the Ball shape sh=shapes(1,:)*pi; % Go to the box shape s=f-6; % Transform to next step df = (sh-r)/steps; arrayfun(@(tx)set(h(tx),'Matrix',xform(r(tx)+df(tx)*s)),1:numblock); end end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
Eric Ludlam / Open The Box
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/14167

function drawframe(f) % Hack to make a good 1st pic for the gallery f = mod(f-2,48)+1; %% Polyhedra Data so we can vectorize % The following polyhedra data can be downloaded from: % https://netlib.org/polyhedra/1 % And was pre-processed into these compressed arrays. % % For Positive Integers: % Convert to char, and offset into the printable character range by % Adding something like '0' to it. % 0 is convenient as you know what the first 10 #s are by sight. % % Decoder D=@(v,c)reshape(v-'0',numel(v)/c,c); % Faces Array F=D('56249<45138;8947;=9:58<>',4); % Compress Doubles: % Identify # of unique values. If that # is small, create reference % array with the unique values. Then compress the indices into the % array of unique values to recreate the original array % If unique values can be represented as colonop easily, do that. % % Vertex Array V=-1.5:0.5:2.5; V=V(D('113333555577993513571357353544444444444444',3)); % Origin of faces so we can offset/fold O=-0.5:0.5:1; O=O(D('231134233112222222',3)); % Rotation Axis R=-1:1; R=R(D('212322221233222222',3)); % Angle of rotation for the solid A=[0 1.5708]; A=A(D('122222',1)); % Children indices for each face to create the graph C=D('300060400000500000200000',4); %% Fold factor % 0 is wide open, 1 is fully solid ff=1-(mod(f-1,24)+1)/24; % Fold factor for this segment sc=(1-ff)*.8+.2; % size of the cube inside the unfolding cube. %% Build child graph using persistent TX1 TX2 R1 R2 if f==48 axes('pos',[0 0 1 1],'clipping','off','Proj','p'); TX = gobjects(0); %% Create the object tree using recursive fcn R1=hgtransform; coi=0; rP(1,R1,O(1,:)); arrayfun(@(fi)xform(TX,ff,fi),1:size(F,1)); TX1=TX; R2=hgtransform; coi=size(F,1); rP(1,R2,O(1,:)); arrayfun(@(fi)xform(TX,1,fi),1:size(F,1)); TX2=TX; %% Make axes nice set(gcf,'color','w'); daspect([1 1 1]); axis([-1.5 2.5 -1.5 2.5 -1 2],'off') view(3) camzoom(1.5) end if f<=24 % Mode 1 ff1=ff; ff2=1; sc1=1; sc2=sc; else % Mode 2 ff1=1; ff2=ff; sc1=sc; sc2=1; end % Configure the 2 cubes based on the mode arrayfun(@(fi)xform(TX1,ff1,fi),1:size(F,1)); arrayfun(@(fi)xform(TX2,ff2,fi),1:size(F,1)); set(findobj(TX1,'type','patch'),'FaceA',ff1^.5); set(findobj(TX2,'type','patch'),'FaceA',ff2^.5); rt1=(1-sc1)*pi*2; rt2=(1-sc2)*pi*2; set(R1,'Matrix',makehgtform('scale',sc1,'translate',[0 0 (1-sc1)*3],... 'zrotate',rt1,'xrotate',rt1)); set(R2,'Matrix',makehgtform('scale',sc2,'translate',[0 0 (1-sc2)*3],... 'zrotate',pi/2-rt2,'yrotate',rt2)); %% Helper Fcns function xform(tx,ff,fi) if A(fi) set(tx(fi),'Matrix',makehgtform('axisrotate',R(fi,:), ff*(A(fi)-pi))); end end function rP(fidx, parent, po) % Recursive function for creating the tree of gfx objects TXT=hgtransform(parent,'Matrix',makehgtform('translate',O(fidx,:))); TX(fidx)=hgtransform(TXT); % Total offset for vertices is local offset plus parent accum offset to=O(fidx,:)+po; % Colors to use co=orderedcolors('gem12'); patch(TX(fidx),'Vertices',V(F(fidx,:),:)-to,'Faces',1:size(F,2),... 'FaceC',co(fidx+coi,:),'EdgeC','w','LineW',2); % Create child nodes for i=1:size(C,2) if C(fidx,i)>0 rP(C(fidx,i),TX(fidx),to); end end end end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
Adam Danz / Pi to 10080 decimal places (polar pi patch)
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/13962

function drawframe(f) persistent x y d pitxt nDecimalPlaces = 10080; if f==1 || isempty(x) digits(nDecimalPlaces+2); piStr = char(vpa(pi)); pDigits = piStr(3:end-1)-'0'; % Assign each digit an angular coordinate based on its value 0:9 theta = ((0:36:324)+linspace(0,36,nDecimalPlaces+1)')*pi/180; ang = theta(sub2ind(size(theta),1:nDecimalPlaces,pDigits+1)); % Compute the length of each line segment; used to set color [x,y] = pol2cart(ang,1); [~,~,d] = uniquetol(hypot(diff(x),diff(y))); d = [d;d(end)]; % Plot line segements using the edge property of a Patch object % Plot segments using patch so we can control transparency within one % graphics object. set(gcf, 'Color','k'); axes(Position = [0 0 1 1]); pitxt = plotpitxt(text()); hold on axis equal padded off % Labels gap = 3; % gap between segments in degrees startpt = ((0:36:324) + gap/2)*pi/180; % starting point of each segment, radians segAng = (0:0.02:1)'.*((36-gap)*pi/180) + startpt; % angular coordinates for segments radius = 1.08; [segx,segy] = pol2cart(segAng,radius); plot(segx,segy,'-w',LineWidth=1,Color=[.8 .8 .8]) % add bounds labels midAng = ((0:36:324)+18) * pi/180; tradius = radius + .08; [tx,ty] = pol2cart(midAng,tradius); text(tx, ty, string(0:9), ..., FontUnits='normalized',... FontSize=0.05, ... Color=[.8 .8 .8], ... HorizontalAlignment='center',... VerticalAlignment='middle'); end nFrames = 48; frameIdx = [1,find(mod(1:nDecimalPlaces,nDecimalPlaces/nFrames)==0)]; plotalpha = @(parent,x,y,color,alpha) patch(parent,'XData',[x(:);nan],'YData',[y(:);nan],'EdgeColor',color,'EdgeAlpha',alpha); cmap = jet(10); for i = frameIdx(f) : frameIdx(f+1) if i==nDecimalPlaces continue end plotalpha(gca,x(i:i+1),y(i:i+1),cmap(d(i),:),0.1) end pitxt = plotpitxt(pitxt); % faster than uistack function pitxt = plotpitxt(h) h.delete pitxt = text(0,0.05,'\pi', ... HorizontalAlignment='Center', ... FontUnits='normalized', ... FontSize = 0.2, ... Color = 'k'); end end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
Ned Gulley / Blender
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/13847

function drawframe(f) c=(sqrt(5)+1)/2; d=2*pi/c; alpha = interp1([0 48],[0 48*2*pi/12],f); theta = (1:600)*d; r = sqrt(theta); theta = theta + alpha; x = r.*cos(theta); y = r.*sin(theta); sz = 30*(1-(1:numel(x))/numel(x)) + 1; clr = sz; scatter(x,y,sz,clr,"filled") axis equal off axis(45*[-1 1 -1 1]) set(gcf,Color=0.3*[1 1 1]) end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Eric Ludlam / Foggy Forest
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries/14422

function drawframe(f) E=5; % Size of one forest environment segment % FogColor Vibe %FC=[0 0 0]; FC=[1 1 1]; % Abbreviations J=@rand; if f==1 set(gcf,'color',FC); % Random placement of trees. Clump neare middle n=40; v1=[rescale(randn(n,1)) J(n,1) rescale(J(n,1),.3,.5)]*E-[E/2 0 0]; % Place a navigable path around zero M=v1(:,1)<=.1; v1(M,1)=v1(M,1)-.2; v1(:,3)=v1(:,3)*.2+.2; % Duplicate so we are in a repeating donut vx=[v1;v1+[0 E 0]]; %B=validatecolor(["#A52A2A" % "#DAA06D" % "#6E260E" % "#954535" % "#7B3F00" % "#80471c" % "#814141" % "#966919"],... % 'multiple'); %G=validatecolor(["#097969" % "#228b22" % "#50C878" % "#4F7942" % "#008000" % "#355E3B" % "#2AAA8A" % "#32CD32"],... % 'multiple'); % How to compress some colors: % % % Turn into flints % U=floor(CLRS*256); % % Turn that into chars, offset forward by SPACE % CH=char(U+' '); % % % Turn this into decode code % A="'"+CH+"'"; % disp("([" + join(A,";") + "-' '])/256;"); % % Compressed version of above: B=(['ÆJJ';'ûÁ';'ŽF.';'¶eU';'›_ ';'¡g<';'¢aa';'·‰9'-' '])/256; G=([')™‰';'B¬B';'pé˜';'o™b';' ¡ ';'U~[';'JË«';'RîR']-' ')/256; for i=1:size(vx,1) %% Tree Trunks N=30; Q=.1; % variation in distance from center RN=12; % n pts in bounding rings rv=[.05 .02]; % Radius values rh=[0 1]; % Radius heights % Random pts on cylinder rt=linspace(0,2*pi,RN+1); rt(end)=[]; T=[J(1,N)*pi*2 rt rt]; h=[rescale(randn(1,N)) ones(1,RN)*rh(1) ones(1,RN)*rh(2)]; % Adjust the radius based on height R=interp1(rh,rv,h); pts=[cos(T).*R sin(T).*R h]'; % triangulate the perfect cylinder tf=convhulln(pts); % Push points in/out with variance of Q D=(1-Q+J(1,size(pts,1))*(Q*2))'; tv=pts.*(D.*[1 1 0]+[0 0 1]); mkP(tf,(tv+vx(i,:).*[1 1 0]).*[1 1 vx(i,3)+.1],i,B,D); %% Tree tops N=150; % Alg for random distribution of pts on a sphere. T=J(1,N)*pi*2; u=J(1,N)*2-1; pts=[0 cos(T).*sqrt(1-u.^2) 0 sin(T).*sqrt(1-u.^2) 0 u ]'; % triangulate the perfect sphere lf=convhulln(pts); % Push points around to make foliage frumphy Q=.15; D=(1-Q+J(1,size(pts,1))*(Q*2))'; lvr=pts.*D; % Scale down into our world and push up into treetops ss=vx(i,3)*.15; llv=lvr.*[.12+ss .12+ss .08+ss]+[0 0 .1]; mkP(lf,llv+vx(i,:),i,G,D); %% Lumpy Ground! N=200; Q=.2; % coordinates T=J(1,N)*2; R=J(1,N)+.05; x=cospi(T).*R*E; y=sinpi(T).*R*E*2+E; % Triangulate the flat disc so we can draw it pv=[x' y']; pf=delaunay(pv); % Variation D=(J(1,size(pv,1))*Q)'; mkP(pf,[pv+.5 D],4,G,D); %% Decorate! set(gca,'position',[0 0 1 1],'vis','off','proj','p'); view(3); daspect([1 1 1]); end end %% Navigate! yp=f/48*E; cp=[0 yp .3]; campos(cp); camtarget(cp+[0 10 0]); camva(90); O=findobj('type','patch'); for i=1:numel(O) addFog(cp,O(i)); end %% Shorten patch creation function mkP(f,v,i,C,D) % f - faces % v - vertices % i - thing index % C - Array of colors to pick from % D - distance array % Create our colors based on D bC=C(mod(i,size(C,1))+1,:); C2=hsv2rgb(rgb2hsv(bC).*[.1 1 .3]); q=bC-C2; fvc=rescale(D)*q+C2; % Create patch and stash colors setappdata(patch('Faces',f,'vertices',v,'EdgeC','n','FaceC','i',... 'FaceVertexCData',fvc),... 'fvc',fvc); end function addFog(cp,p) v1=p.Vertices-cp; % Center around camera position. clr=getappdata(p,'fvc'); % Compute depth from camera, and rescale as 0-1 B=rescale(hypot(hypot(v1(:,1),v1(:,2)),v1(:,3)),'InputMin',0,'InputMax',5).^.25; % Treat fog as a semi-transparent white on top of the patch. % The depth implies the volume of fog you need to see through to get to the vertex. set(p,'FaceVertexCData',FC.*B+clr.*(1-B)) end end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
完
比赛还有12天才结束,感兴趣的快去参加:
https://ww2.mathworks.cn/matlabcentral/communitycontests/contests/6/entries
-
相关阅读:
C++前缀和算法的应用:摘水果 原理源码测试用例
如何为集中认证安装OpenLDAP服务器
YOLOv5算法改进(11)— 在C3模块中添加注意力机制(包括代码+添加步骤+网络结构图)
flink-sql查询配置与性能优化参数详解
【Java成王之路】EE初阶第十九篇: 前端三剑客 CSS基础篇
C语言,求两个数的二进制表达中,有多少个位数不同
解决Opencv dnn模块无法使用onnx模型的问题(将onnx的动态输入改成静态)
【Kafka】Kafka生产者数据重复、数据有序、数据乱序-07
Mybatis - 核心配置解读
刷题 BFS 广度优先算法 : 大胖子走迷宫 (python, java)
- 原文地址:https://blog.csdn.net/slandarer/article/details/134521708
