【数据结构】AVL树的插入和自平衡调整

AVL树是最早发明的自平衡二叉查找树。在AVL树中，任一节点对应的两颗子树的最大高度差为1，因此他被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是 $$O(\log n)$$增加和删除操作后可能需要通过一次货多次旋转来实现平衡

AVL树结构

• 可以是空树
• 任一节点对应的两颗子树的最大高度差为1

下面的两颗树就不是AVL树

50节点的左子树高度为2右子树的高度为0；60节点左子树高度为3左子树高度为1，不满足条件。

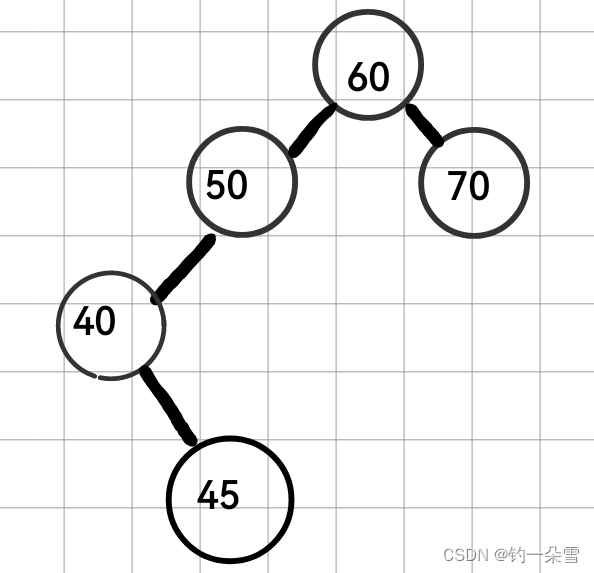
50节点的左子树高度为2右子树的高度为0；60节点左子树高度为3左子树高度为1，不满足条件。

下面这棵树是AVL树

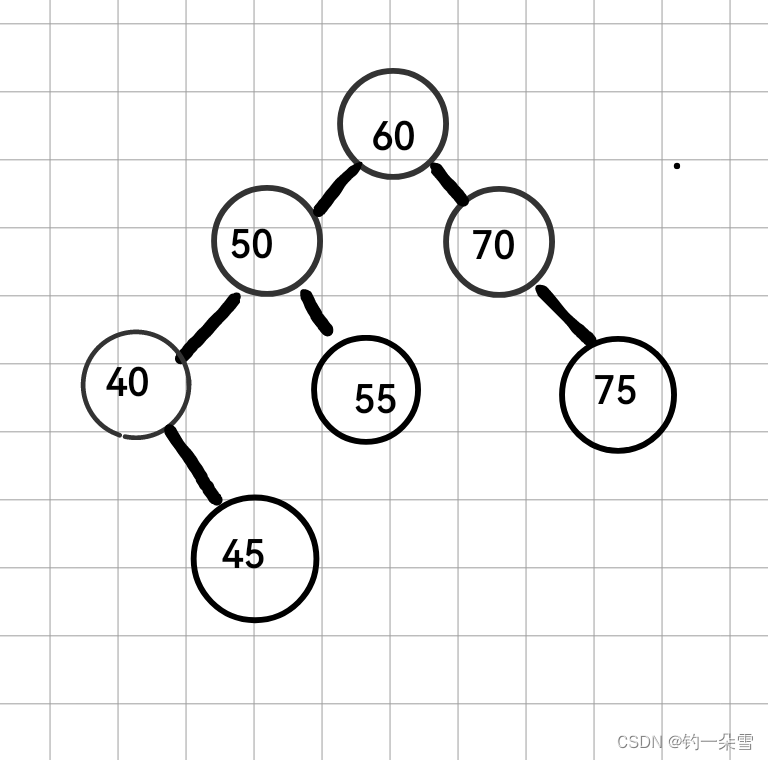
节点结构

typedef struct AVL
{
	int data;
	int bf;				//平衡因子
	struct AVL* left;
	struct AVL* right;
	struct AVL* parent;
}AVL;
1
2
3
4
5
6
7
8

平衡因子为右子树和左子树的高度差

AVL树的插入

AVL树插入节点的步骤

1. 按照二叉搜索树的插入方法找到待插入节点
2. 找到待插入节点后，将节点插入树中。
3. 更新平衡因子，判断是否需要继续更新/旋转
4. 如果需要旋转，判断旋转类型

更新平衡因子的规则

• 如果插入节点是parent的左孩子，则parent的平衡因子–
• 如果插入节点是parent的右孩子，则parent的平衡因子++

更新完一个节点的平衡因子后的判断

• 如果parent平衡因子为1或-1，则要继续往上更新
• 如果parent的平衡因子为0，则无需继续往上更新平衡因子
• 如果parent的平衡因子为2或-2，则表明以parent为根的子树已经不平衡，需要进行旋转。
  解释
• 因为只有parent的平衡因子为0时经过++或者–操作才会变成1/-1，这说明插入后parent的左子树或者右子树变高了，那么以parent为根的子树变高了，从而影
  响了parent的父节点的平衡因子，所以要往上更新。
• 因为只有parent的平衡因子为-1/1时经过++或者–操作才会变成0，说明插入前parent左右子树高度不一，新节点插入到了较矮的子树上，那么插入后并没有影响以parent为根的树的高度，从而不会影响parent的父节点的平衡因子。

判断旋转类型

向上更新的过程中必然指向下面的逻辑

cur=parent;
parent=parent->_parent;
1
2

那么根据cur的平衡因子和parent的平衡因子就可以判断旋转类型

如图所示插入节点13，向上更新parent的平衡因子，节点12的平衡因子由0—>1
节点15的平衡因子由1—>0，结束平衡因子的更新。

bool Insert(AVL** root, int data)
{
	if (!(*root))
	{
		*root = CreateNode(data);
		return true;
	}

	AVL* cur = *root;
	AVL* parent = NULL;
	//找
	while (cur)
	{
		if (data > cur->data)
		{
			parent = cur;
			cur = cur->right;
		}
		else if (data < cur->data)
		{
			parent = cur;
			cur = cur->left;
		}
		else
			return false;
	}
	cur = CreateNode(data);
	//插（左/右）
	if (data < parent->data)
	{
		parent->left = cur;
		cur->parent = parent;
		/*parent->bf--;*/
		/*现在还不是更新平衡因子的时候*/
	}
	else
	{
		parent->right = cur;
		cur->parent = parent;
		/*parent->bf++;*/
		/*现在还不是更新平衡因子的时候*/
	}
	//更新平衡因子
	while (cur != *root)
	{
		if (cur == parent->left)
		{
			parent->bf--;
		}
		else
		{
			parent->bf++;
		}
		
		//需要继续向上找
		if (parent->bf == 1 || parent->bf == -1)
		{
			cur = parent;
			parent = parent->parent;
			//结束
			if (parent == NULL || parent->bf == 0)
				break;
		}
		
		//需要旋转
		if (parent->bf == 2 || parent->bf == -2)
		{
			if (parent->bf == 2)
			{
				if (cur->bf == 1)
					RotateL(parent);
				else if(cur->bf == -1)
					RotateRL(parent);
			}
			else if(parent->bf == -2)
			{
				if (cur->bf == 1)
					RotateLR(parent);
				else if(cur->bf == -1)
					RotateR(parent);
			}
		}
	}
	return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

旋转处理

左单旋

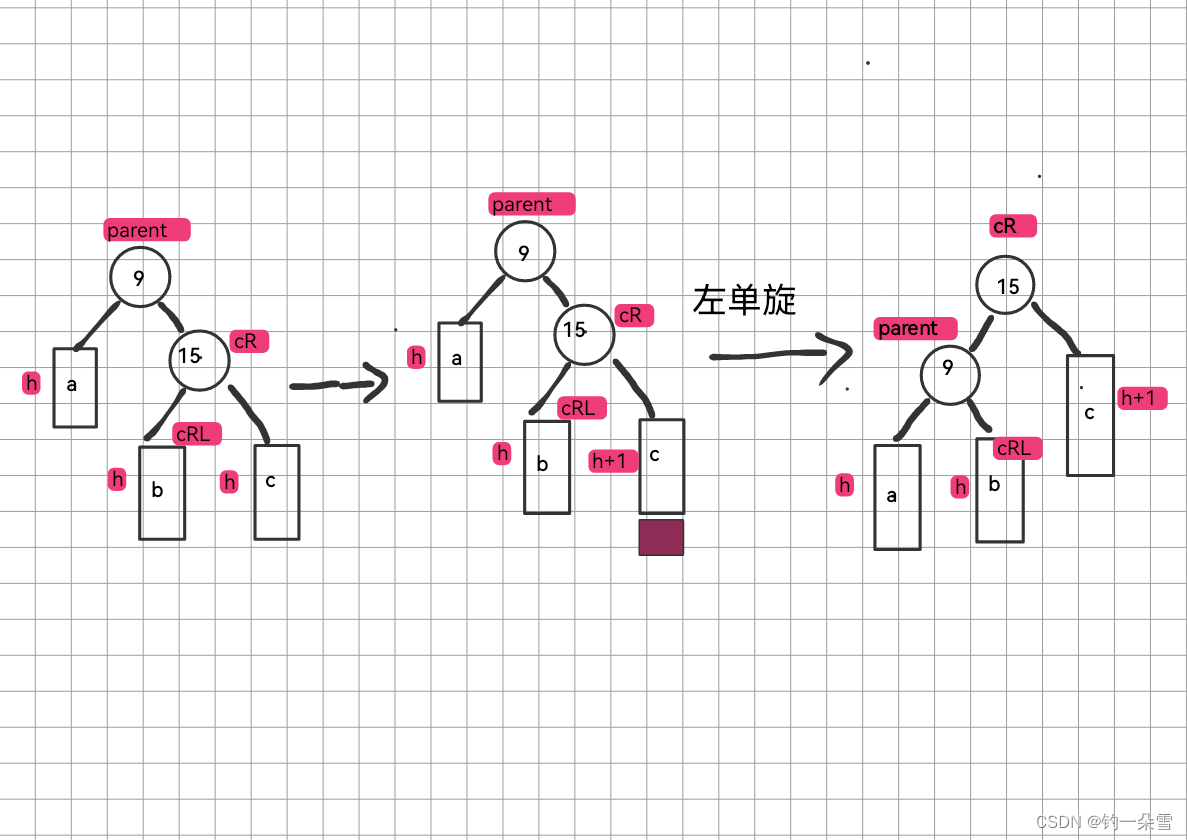
步骤

1. cR的左子树作为parent的右子树
2. parent成为cR的左子树
3. cR成为子树的根
4. cR插入到树中
5. 更新平衡因子

右单旋

步骤

1. cL的右子树成为parent的左子树
2. parent成为cL的右子树
3. cL成为子树的根
4. cL插入到树中
5. 更新平衡因子

左右单旋

插入节点

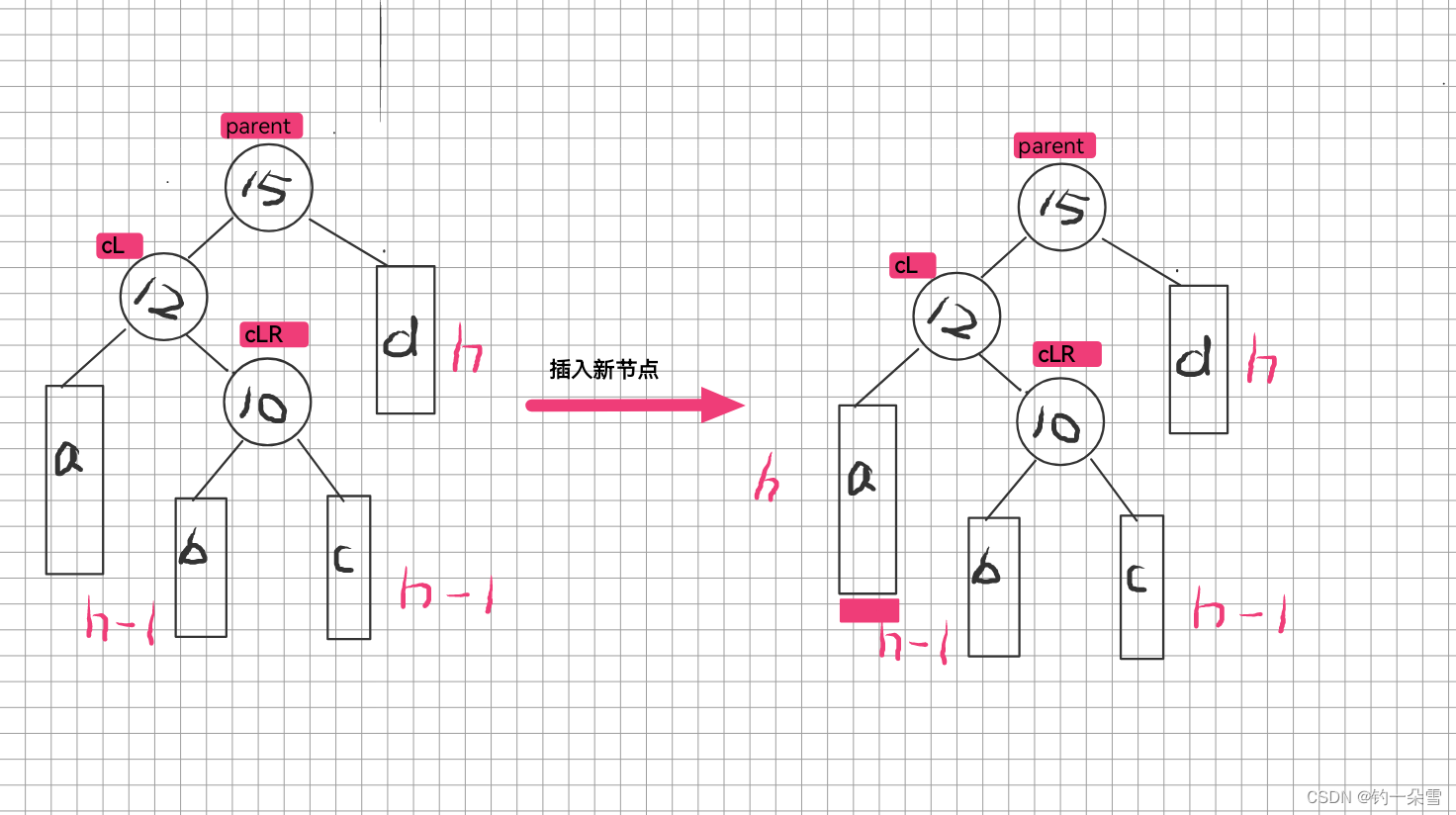
左单旋

右单旋

平衡因子更新的三种情况

2.

3.

右左单旋

插入节点

右单旋

左单旋

void RotateRL(AVL* parent)
{
	AVL* cR = parent->left;
	AVL* cRL = cR->right;
	int bf = cRL->bf;
	RotateR(cR);
	RotateL(parent);
	//更新平衡因子
	if (bf == 1)
	{
		parent->bf = -1;
		cR->bf = 0;
		cRL->bf = 0;
	}
	if (bf == 0)
	{
		parent->bf = 0;
		cR->bf = 0;
		cRL->bf = 0;
	}
	if (bf == -1)
	{
		parent->bf = 0;
		cR->bf = 1;
		cRL->bf = 0;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

验证平衡二叉树

平衡二叉树是一种加了平衡限制的二叉查找树，所以通过中序遍历可以验证是否为一颗二叉查找树。通过后序遍历，从叶子节点开始获取每个节点左右子树的高（以该节点为根的子树高为 左右子树中高度的较大值 + 1）

bool isBalanced(AVL* root, int* phight)
{
	if (root == NULL)
	{
		return true;
	}
	int leftHight = 0;
	if (isBalanced(root->left, &leftHight) == false)
		return false;
	int rightHight = 0;
	if (isBalanced(root->right, &rightHight) == false)
		return false;

	/*if (rightHight - leftHight != root->bf)
		printf("平衡因子设置异常\n");*/
	*phight = MAX(leftHight, rightHight) + 1;

	return abs(rightHight - leftHight) < 2;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19