-
论文阅读:“基于特征检测与深度特征描述的点云粗对齐算法”
摘要
点云对齐是点云数据处理的重要步骤之一,粗对齐则是其中的难点。近年来,基于深度学习的点云对齐取得了较大进展,特别是 3DMatch 方法,能够在噪声、低分辨率以及数据缺失的条件下取得较好的对齐效果。3DMatch 采用随机采样的方式产生待匹配点,当采样点个数较少时会导致匹配率较低,因此对齐效果不佳。为此,利用 ISS 特征点检测代替随机采样,然后以 3DMatch 为特征点生成描述符,最后通过匹配特征描述符实现数据对齐。
由于 ISS 特征点检测具有良好的重复性,同时 3DMatch 能够提供具有高区分度的描述符,因此该方法大大提高了匹配的鲁棒性和准确性。实验结果表明,与随机采样相比,特征点采样在初始点云无噪、弱噪和强噪的情况下对齐效果更好、鲁棒性更强,并且在粗对齐效果相似的情况下,所需特征采样点的个数仅为随机采样点个数的10 %,极大地提高了对齐的效率。
简介
点云对齐是三维模型重建的关键步骤之一。特别是粗对齐,需要在不清楚两片点云的相对位置关系的情况下,通过找到一个变换关系来使两片点云的共同部分较好地重叠在一起。一个好的粗对齐结果能为后续的精细对齐提供良好的初始位置,并避免精细对齐陷入局部最优解。
3DMatch 利用 RGB-D 重构结果生成数百万个对应的标签,对其进行训练后能够得到鲁棒性好、泛化能力强的特征描述符。通过寻找生成特征描述符的匹配关系,即可实现粗对齐。但该方法中的待匹配点是通过随机采样获得的,对于规模较大的点云数据,采样点的重复性差、匹配率低,从而导致粗对齐效果不佳。
针对上述问题,这篇文章基于 ISS 特征检测的方法,对原始点云进行特征点提取,以提高待匹配点的重复性,同时采用深度特征描述符来改善待匹配点的相似度量。
相关工作
粗对齐
粗对齐算法大致可分为两类:一类为传统的粗对齐算法;另一类为基于深度学习的粗对齐算法。
传统的粗对齐算法
4PCS 的基本思想来源于 RANSAC 算法,其优化了寻找两片点云“对应点”的策略。基于共面四点对的仿射不变性,该算法从源点集中选取共面的四点作为基面,然后在目标点集中找到所有与基面近似一致的共面四点对,以此进行粗对齐。该算法尽管能够取得较好的对齐效果,但是在目标点集中找到的与源点集基面对应的 4 个点会存在误匹配点,而剔除错误点会耗费大量的时间,从而降低了对齐效率。
Super 4PCS 算法改进了 4PCS 算法,通过添加额外的约束条件来滤除潜在的错误点对,从而得到了与基面对应的唯一四点集,并加快了算法的执行速度。但是 Super 4PCS 对噪声较大的点云的对齐效果不佳,且对齐时长不稳定。
SAC-IA 算法首先分别计算源点云和目标点云的 FPFH(Fast Point Feature Histograms)特征描述子,然后在目标点云中查找与源点云中采样点具有相似 FPFH 特征的点,最后从这些相似点中随机选取一个点作为源点云与目标点云的对应点,并通过 Huber 惩罚函数计算距离误差和,完成对齐。但是,SAC-IA 在点云数量较多的情况下,计算 FPFH 特征较慢,算法效率低,因此需要对点云进行下采样处理,以减少点的数量,但这会造成部分特征点丢失,从而降低对齐的准确度。
基于深度学习的粗对齐算法
3DShapeNets 将深度学习引入三维建模中,通过计算三维数据的深层特征来提取全局特征,其抗噪性能好,但是细节区分能力差,因此仅当数据重合度很大时才能得到很好的对齐效果。
3DMatch 利用 RGB-D 重构结果中的数百万个正负标签,通过孪生网络结构的 3D 卷积神经网络,训练出鲁棒性高且泛化能力强的描述符,在新的场景下依然能实现粗对齐。
相比传统算法,基于深度学习的对齐算法能够利用训练好的权重为局部特征快速生成描述符以进行对齐,并且对噪声、离群点具有鲁棒性。
特征检测及描述符构建
特征检测及特征描述符构建是三维模型粗对齐中重要的一环。常用的特征检测方法有 SIFT 特征检测、NARF 特征检测、Harris3D 角点检测和 ISS 特征检测。
SIFT 特征检测通过在空间尺度中寻找极值点,来提取其位置、尺度、旋转不变量,因此基于 SIFT 特征检测提取的特征点具有鲁棒性。SIFT 描述符通过对特征点的周围图像区域进行分块,来计算尺度空间内的 128 维向量,并将其作为该区域的特征。但是,SIFT特征检测多适用于带有颜色映射的点云模型。
NARF 特征检测对法向量的估计比较稳定,该算法将点云数据转换成 2D 深度图,其计算量小于直接操作点云数据的方法。NARF 描述符能够描述物体表面以及外部空间形状,对特征点建立唯一的一个局部坐标系并通过距离函数区别特征,从而找到匹配对。但是,NARF 算法适用于较为规则的深度图像。
Harris3D 角点检测是 2D Harris 算法的一种延伸。该算法借助离散点云的法向信息构造协方差矩阵,并根据角点响应函数计算点云中每个角点的响应值,最后将响应值大于设定阈值的局部极大值点判定为特征点。Haris3D 角点检测具有很强的旋转不变性,但通过该方法提取到的特征点数量不如 ISS 特征检测提取到的多,而且在平滑曲面上的差距更为明显。另外,Harris3D 角点检测的效率也远不如 ISS 特征点检测。
ISS 特征检测首先构建基于当前点的局部坐标系,并在该坐标系下对邻域点协方差矩阵进行特征分解,然后得到协方差矩阵的特征值。特征值对应的椭球形态是对邻近点分布状态的抽象总结,因此根据椭球的 3 个主方向的大小关系判断该点是否为特征点。基于ISS特征检测提取的特征点数量多、重复性好,而且对噪声具有鲁棒性,结合 3DMatch 算法,对特征点生成对应的描述符来寻找匹配对,可以较好地实现数据对齐。
本文算法
首先分别对源点云和目标点云进行 ISS 特征检测,然后利用 3DMatch 网络对特征点生成对应的 512 维 DNN 描述符,最后结合 KD-Tree 搜索,对两点的描述符计算 L2 范数来判断这两个点是否为匹配对,并通过 RANSAC 算法求得最优的旋转平移矩阵。
ISS 特征检测
ISS 特征检测算法首先对点云上的每个点都定义一个局部坐标系,然后通过协方差矩阵建模,求得 3 个特征值和特征向量。这 3 个特征值和特征向量定义了一个椭球空间,其中,特征值代表椭球轴的长度,特征向量代表以该点为中心的椭球的 3 个主方向。若某一点的 3 个主方向大小相近,则表明当前点处曲面起伏很大,进而可以判定该点为特征点。
RANSAC 算法
虽然基于ISS特征检测算法提取的点都是特征点,但因受到噪声等影响,特征点集中也会包含错误数据,因此需要对其进行滤除。而 RANSAC 算法能够通过模型估计将数据区分为内点和外点,并能剔除外点,即错误点,因此采用 RANSAC 算法。
RANSAC 算法的基本假设是样本中既包含正确数据又包含错误数据,首先随机选择样本数据集的子空间生成模型估计,测试和评估剩余样本数据集中的点,符合该模型的点称为内点,反之为外点,然后通过不断迭代,最终找出内点个数最多、误差最小的单应性矩阵。此时认为所有的外点均为错误数据并将其滤除。
3DMatch 算法
3DMatch 是一种数据驱动模型,该模型采用自监督的特征学习方法,利用局部体素网格的描述符来建立三维数据之间的对应关系。3DMatch 网络结构如下图所示:
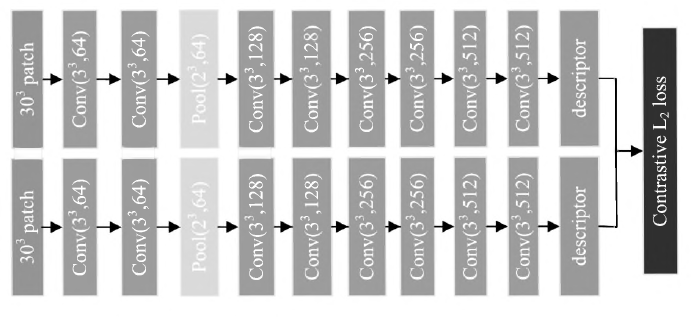
利用 3DMatch 进行点云对齐的具体过程如下:- 对目标点云和源点云进行随机采样,并以每个采样点为中心提取大小为 30 × 30 × 30 30\times 30 \times 30 30×30×30 的体素网格来代表该点,其中每个小体素格子的具体尺寸根据输入点云模型的大小进行自适应调整;
- 计算网格中每个小体素格子的 TDF 值,这些值代表该体素中心与最近的 3D 表面之间的距离,再将这些 TDF 值归一化(1 代表在点云表面上,0 代表远离点云表面);
- 以该点的体素网格作为神经网络的输入生成对应的特征描述符;
- 通过 L2 范数进行相似性度量并结合对比损失函数建模,从而判断两点是否为匹配对。
实验结果
无噪声情况下随机采样与特征检测算法的比较:
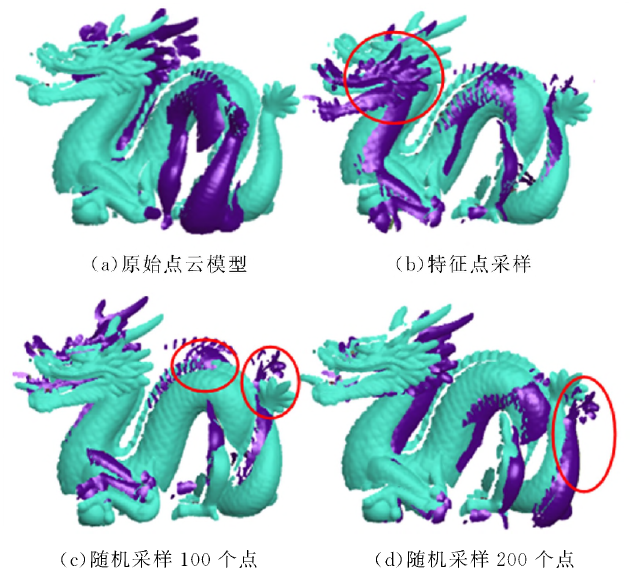
弱噪声情况下随机采样与特征检测算法的比较:
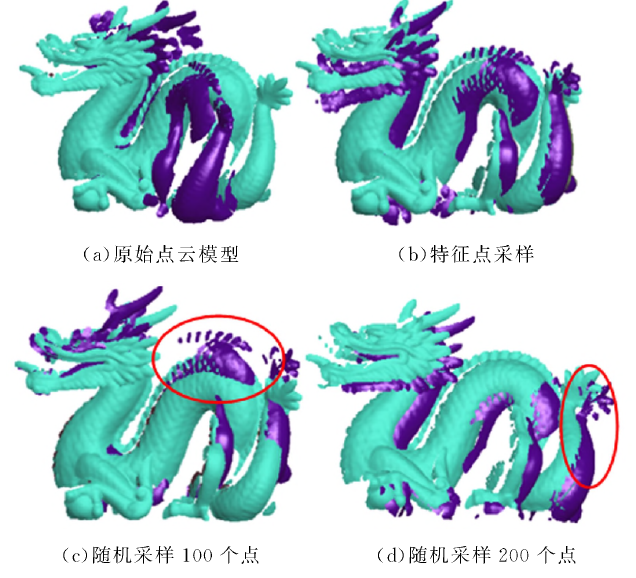
强噪声情况下随机采样与特征检测算法的比较: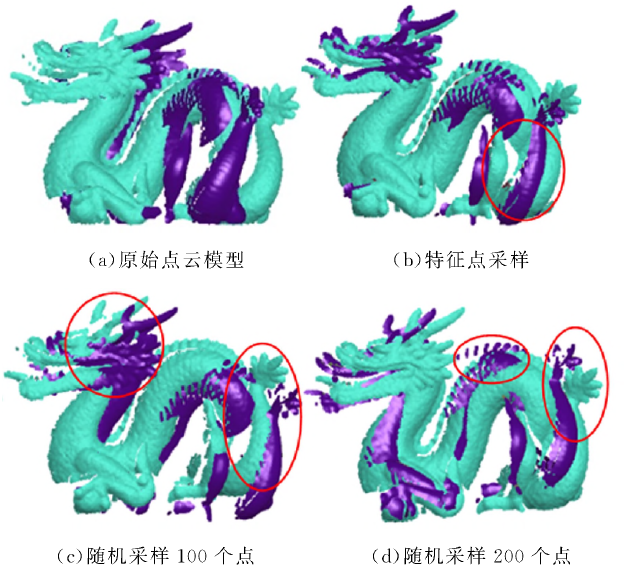
参考文献
[1] 史文凯,张昭晨,喻孟娟,吴瑞,聂建辉,基于特征检测与深度特征描述的点云粗对齐算法,计算机科学。DOI:10. 11896/jsjkx. 191000069
-
相关阅读:
vue3 tsx语法
热门项目!知识付费小程序源码系统 带完整的安装代码包以及安装部署教程
机器人龙头概念股一览,机器人龙头股
linux简介
Uni-App中的u-datetime-picker时间选择器Demo
基于蒙特卡洛的电动车有序充放电(Matlab代码实现)
他又来了,.net开源智能家居之小米米家的c#原生sdk【MiHome.Net】1.0.0发布,快来打造你的私人智能家居吧
提升用户留存率:如何集成直播实时美颜SDK来增强用户体验
大尺寸图像分类检测分割统一模型:Resource Efficient Perception for Vision Systems
在 Android Studio Java 项目里混合 Kotlin 编程
- 原文地址:https://blog.csdn.net/myDarling_/article/details/134513205