李沐深度学习 4.5 权重衰减的知识梳理与课后习题

嗨嗨嗨，欢迎来到小明的知识总结和知识梳理，
如果需要学习打卡和讨论的童鞋请进入扣扣裙：908720512，打卡到达一定天数或讨论的内容很深入可以获得小礼品哦！！！！快来吧！！！！最重要的是如果这一章的代码报错，也可以在群里得到解答！！！！

声明：以下解答都是笔者自己自学后的理解，如果不妥请指正

4.5 权重衰减

我们先来看看书上的描述：在训练参数化机器学习模型时，权重衰减（weight decay）是最广泛使用的正则化的技术之一，它通常也被称为l2正则化，这项技术通过函数与零的距离来衡量函数的复杂度。

笔者的理解：传入函数的自变量的值越大，那么函数就越复杂，计算所花的成本就越高，而权重w和损失函数loss的关系就是这样，因此我们就想要w尽量的小，就要给他一个范围来限定。

我们来看看表达式，（注意这里的l2范数的表达式右上角有一个平方，为什么要有一个平方呢？李沐深度学习的书里讲了答案，希望大家能去看看，自己动手丰衣足食嘛）：

图一

但是这样写有一个问题，我们如何用代码来表示这一个式子呢？在书中沐神也给了一个式子：

图二

如何来理解这个式子呢？笔者认为λ是一个超参数，比如：你的λ是无穷大的话，那么你要想这个表达是尽可能的小，那么你就要让你的w尽可能的小，那么既然图一和图二是等式，那么λ和θ的关系是什么呢？当θ为0的时候，λ就是无穷大，那么要想整个表达式的值最小，就要w取到0，也就是；当θ为无穷大的时候，λ就是0，就意味着，w的值可以任意取。不知道这样说读者是否可以理解，笔者认为这一章的难点就在这。如果还有疑问可以进入扣扣裙：908720512。
那么梯度下降的公式就可以变成：

图三

笔者在看到这个公式和后面给的代码的时候有个疑问，既然梯度下降的公式变了，那么优化器为什么没有改变，因为在第三章中沐神，给出的优化器的作用就是来更新参数。那么按照道理来说也需要一个相应的优化器吧。其实这就是固定化思维带来的坏处，如果当时想到可以在其他地方实现，也不会困扰我那么久。
言归正传：梯度更新最开始规则的是w=w - lr * w，然而图三的思想就是限制w，那么我们能不能不改动原始代码和函数的基础上来实现呢？我认为改变损失函数是最简单的做法。因为通过图二求偏导求出来的w，已经对w进行了限制，也就是说通过图二求偏导求出来的w，再加上最开始的sgd的参数更新方法就等价于图三。
如果你坚持看到这，恭喜你这一章最难的点你已经度过了。

一些个人理解：

1.权重衰减就是l2范数正则化，也就是惩罚参数w
2.防止过拟合的的思路：（1）降低模型的复杂度，（2）减小模型参数的取值范围

完整可运行的代码

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)


def init_params():
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
    b = torch.zeros(1, requires_grad=True)
    return [w, b]

def train(lambd):
    w, b = init_params()
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
    num_epochs, lr = 100, 0.003
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    for epoch in range(num_epochs):
        for X, y in train_iter:
            # 增加了L2范数惩罚项，
            # 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
            l = loss(net(X), y) + lambd * l2_penalty(w)
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size)
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数是：', torch.norm(w).item())

# lambd就是确定图二中的超参数
train(lambd=0)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

课后习题

1.在本节的估计问题中使用λ的值进行实验。绘制训练和测试精度关于λ的函数图。观察到了什么？

def train_2(num):
    w, b = init_weights(num_inputs)
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
    num_epochs, lr = 100, 0.03
    animator = d2l.Animator(xlabel='lambda', ylabel='loss', yscale='log',
                            xlim=[0.1, 1],legend=['train', 'test'])
    for lamda in np.arange(0, num + 0.1, 0.1):
        for i in range(num_epochs):
            for X, y in train_iter:
                l = loss(net(X), y) + lamda * l2_penalty(w)
                l.sum().backward()
                d2l.sgd([w, b], lr, batch_size)

        animator.add(lamda, (d2l.evaluate_loss(net, train_iter, loss),
                                    d2l.evaluate_loss(net, test_iter, loss)))
    print('w的l2范数是', torch.norm(w).item())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

结果：

从曲线本身来讲，
（1）train是呈现递增，而test是呈现递减。
（2）λ越小train和test的loss值差距就越大，λ越大则反过来
那么超参数的选择是不是就越大越好呢？不是的，笔者认为这就和下面这张图选择类似，我们应该选在中间：

2.使用验证集来找到最佳值λ。它真的是最优值吗？
回答：我认为并不是这样，笔者在第一题中回答了这个问题，应该选择中间的点。

3.如果我们使用l1范数作为我们选择的惩罚，那么更新方程会是什么样子？

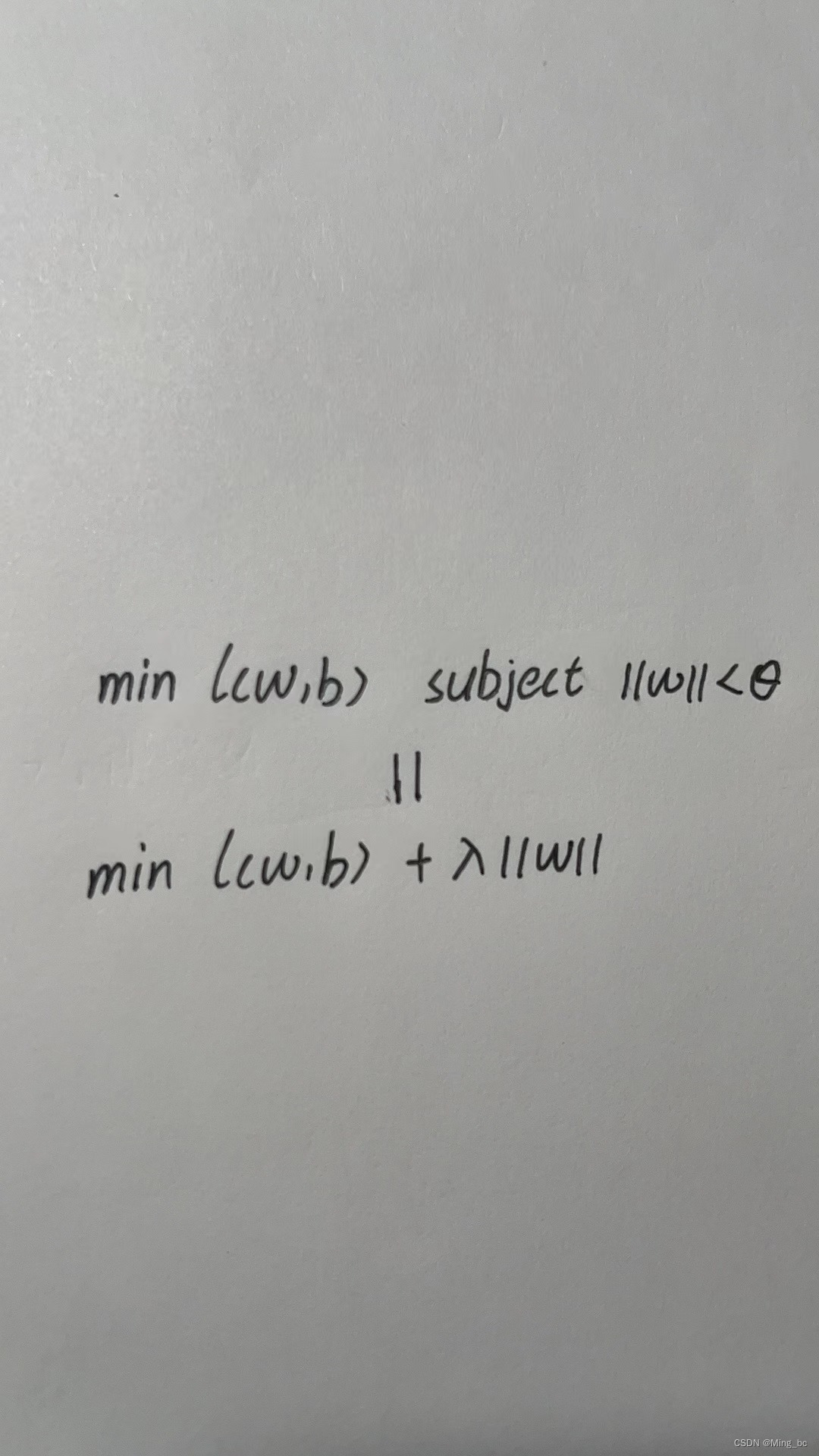
4.我们知道那边。能找到类似的矩阵方程吗（见 2.3.10节 中的Frobenius范数）？

5.回顾训练误差和泛化误差之间的关系。除了权重衰减、增加训练数据、使用适当复杂度的模型之外，还能想出其他什么方法来处理过拟合？
回答：加入dropout层，随机冻结一些参数

6.在贝叶斯统计中，我们使用先验和似然的乘积，通过公式得到后验。如何得到带正则化的？

笔者在写代码中遇到的坑

1.range()方法没有办法生成0到1之间的浮点数，他只能生成整数。