DDPM的学习

Denoising Model

• 首先是宏观理解一下

Denoising Model 的输入

• 去噪很多步，用的是同一个Denoising Model，但是输入图片可能差距很大。解决方法：给Denoising Model多输入一个变量，表示现在的去噪阶段，让Denoising Model根据不同的噪音程度做出不同反应
  

Denoising Model内部结构

• 在其内部有一个噪音预测模块，根据输入的图片和去噪阶段，预测这张图片的噪声是什么，得到这个噪声后，让输入图片减去这个噪声，就是这个Denoising Model的输出
• 为什么要预测噪声呢，如果直接输入图片然后输出去噪后的图片，那这意味着模型可以画那个输出图片了，这是非常困难的，而预测噪音相对来说就比较容易
  

如何训练Denoising Model

• 训练Denoising Model就是训练Noise Predicter，那就要有真实的噪音，这样Noise Predicter才能学习如何预测噪音。
  
• 这个训练数据是人为创造的(拿一张图片，自己加噪声),这个过程叫Forward Proces(Diffusion Process)
  
• 这时候就有Noise Predicter的训练资料了,如下图的input图片和阶段2是Noise Predicter的输入，而它的输出就应该是那个真实的噪声，训练Noise Predicter让它的输出接近这个噪声
  

对于Text-to-image

• 还是需要文字标签和图片两种信息的资料

• 训练集数据集,像midjourney、stable diffusion、DALL都是用的第三个数据集50多亿张训练图片
  

• 直接将文字输入到Denoising Model
  

• 而Noising Predicter部分也直接加入文字资料
  

• 训练部分的修改，也是在去噪过程中将文章资料给Denoising Model，这代表Denoising有三个输入
  

• 下面是详细过程

DDPM的算法流程

训练

1. 首先从数据库得到一个清晰的图片x0
2. 然后随机从1到T中得到一个t，代表要加噪的程度(真实操作是直接一步到位，不会一步一步添加噪声，直接到这个t的噪音层次)
3. 然后从标准正态分布中采样一个噪音ε
4. αt中的t是上面的t，t越大αt越小，αt是0到1之间的值；这里括号内的意思是给x0和ε分别赋权重，然后把两个图片加和在一起；εθ就是Noise Predicter，在εθ输入含噪声图片和t，然后让它输出预测的噪音，再拿真实的噪音减去预测的，最小化这个差值
   • αt是一个用于控制噪声注入量的超参数，是在训练前就设定好的，他是一个逐渐减小的序列，目的是让模型逐渐适应越来越大的噪声。
     

• 想象中加噪音是一点一点加的，但实际上是一步到位
• 真实高斯噪声和模型预测的高斯噪声通过均方误差(MSE)来计算损失，然后更新梯度

生成

1. 首先从标准正态分布中采样一个高斯噪声
2. 然后从第T阶段一步一步像原始图像推进
3. 再采样一个高斯噪声Z用来模拟T-1步的方差，即在生成过程中加入噪音会生成的更好
4. 第四步的公式，代表生成了第Xt-1阶段的图像，等式右边的第一项是去噪模型生成εθ(高斯噪声)，其它都是已知量，再加上Z，形成的新的高斯噪声，从这上面随机采样可得到Xt-1的图片

前向传播

• 设从数据集得到的图片为X0，在逐渐加噪的过程中，可由Xt-1得到Xt,εt是这一步骤所加的高斯噪声
  
• 由Xt-2得到Xt,εt-1和εt分别是两步的高斯噪声，都服从标准正态分布
  
• 上面公式先忽略高斯噪声的系数，其实就是两个高斯噪声相加，也就是叠加它们的概率分布，下面是两个正态分布的叠加公式
  
• 将εt-1和εt的系数看为一个常数，正态分布乘以一个常数，它的均值μ和标准差σ都乘以这个系数，由于εt-1和εt都服从标准正态分布，所以它们的均值为0标准差为1，所以εt-1和εt和其对应系数表示的正态分布分别为
  
• 根据正态分布叠加公式可得综合εt-1和εt正态分布的新的正态分布的均值和标准差，从这个新的正态分布上采样得到的随机数，就等同于之前两个带系数的εt-1和εt正态分布采样的和，也就是直接在这个上采样，就替代了那两个
  
• 也就是拿一个标准正态分布，再乘以新的系数，形成新的正态分布，也就是用这个新的正态分布就代替了前面两个
  
• 然后可继续将Xt-2换为Xt-3等等重复进行，使用数学归纳法可得
  
• 其中的αtαt-1…α1很长，用其它符号代替，可得下面公式，这样就可以从X0一步到Xt，一次把高斯噪声加完
  

反向传播

贝叶斯定理

• 现已知男孩抓到娃娃机了，问在抓到的这个娃娃是在公交站那里抓到的概率是多少，在地铁站旁边抓到娃娃的概率是多少
  
• 贝叶斯公式
  
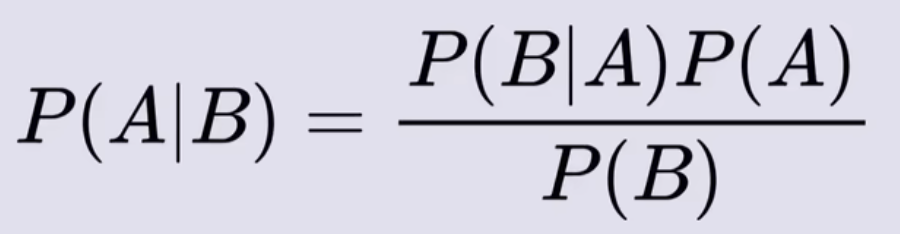
• P(A)和P(B)是两个随机概率，P(B|A)是A发生情况下B发生的概率，P(A|B)是B发生情况下A发生的概率(也可以理解为在B发生的情况，B的发生是由A发生所引起的概率)
  • 在刚才的例子中P(A)指小明坐公交或地铁的概率，是基于之前的经验称为先验概率prior
  • P(A|B)同样指小明坐公交或地铁的概率，但是是在B事件发生后对先验概率P(A)的修正，所以称为后验概率posterior
  • 上面修正的基础是因为看到了B事件的发生，所以B事件称为证据Evidence
  • P(B|A)表示在A事件发生前提下B事件很有可能发生，所以称为似然Likelihood，它的值可以看作为B事件对A事件的归因力度，即当P(B|A)值越大时，B事件就提供更强的证据支持A事件，所以P(B|A)也可以理解为B事件对A事件的证据强度
    

反向传播公式推导

• 由于Xt-1到Xt的加高斯噪声是随机事件，所以从Xt到Xt-1也是一个随机事件，套用贝叶斯公式可得
  
• 其中的P(Xt-1)和P(Xt)分别表示Xt-1和Xt时刻的概率，也就是从X0原图得到它们的概率(加高斯噪声可以看做一个随机事件),则改写公式可以写为P(Xt-1|X0),P(Xt|X0)，但X0可以认为百分百的事件
  
• 为了匹配给另外两项也加上X0的条件,表示在相同的X0条件下，其实可以忽略它们，至此只需要求解右边式子就能得出Xt条件下Xt-1的概率
  
• 概率和高斯噪声的转换：P(Xt|Xt-1,X0)对应的高斯噪声如下图所示
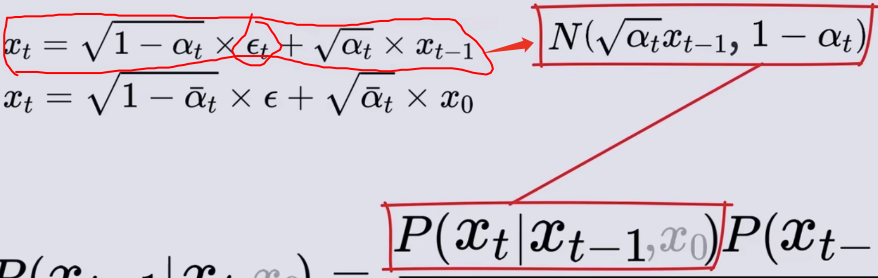
  • εt是标准正态分布，它的均值是0，标准差为1，乘以一个系数均值和标准差都要乘，然后再加上一个常数，只需要均值加即可，可得下面新的高斯噪声，这个高斯噪声就是给定Xt-1时刻，对应的Xt时刻概率分布
    
• 同理可得其它两项对应的正态分布
  
• 当正态分布的均值和方差确定后，就可以把他们写成正态分布的 概率密度函数形式
  
• 再将这三个概率密度函数带入到贝叶斯公式中
  
• 我们的目标是求解给定Xt条件下Xt-1的概率，实际上它也是正态分布，接下来要做的是将等式右边变换为Xt-1的概率密度函数的形式，最终可以变为下式
  
• 所以P(Xt-1|Xt,X0)对应的正态分布如下
  
• 我们的最终目标是利用Xt到前一时刻Xt-1的关系，从XT开始不断使用这个关系迭代到直到X0，X0是需要求得的结果，但现在却出现在P(Xt-1|Xt,X0)的概率分布中，说明上式存在问题。
  • 解决方法：之前已经求得了X0到Xt的公式，将这个公式用Xt表示X0，代入上式即可
    
• 最后得到下面公式：它表示的就是，对于任意的Xt时刻的图像，都可以认为是从某个X0原图直接加噪得来的，而只要知晓了从X0到Xt加入的高斯噪声ε，就能得到它的前一时刻Xt-1的概率分布
  
• P(Xt-1|Xt,X0)的均值可以再化简为如下图
  
• 所以去噪模型的输出是下面的东西
  
• 上面的P(Xt-1|Xt,X0)的最终化简其实就是生成阶段的那个公式，因为红框内部分是均值，所以要加上一个高斯分布代表考虑了方差
  
• 损失就是下面这个，主要就是预测的噪声分布和真实的噪声分布的差最小
  
  参考资料：李宏毅老师的DDPM
  B站视频：https://www.bilibili.com/video/BV1tz4y1h7q1/?
  deep_thoughts视频：https://www.bilibili.com/video/BV1b541197HX/