SDUT OJ《算法分析与设计》搜索算法

A - 子集和问题

Description

子集和问题的一个实例为〈S,t〉。其中，S={  x1 ， x2 ，…，xn }是一个正整数的集合，c是一个正整数。子集和问题判定是否存在S的一个子集S1，使得：
 

。
试设计一个解子集和问题的回溯法。
对于给定的正整数的集合S={  x1 ， x2 ，…，xn }和正整数c，计算S 的一个子集S1，使得：
 

。

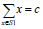
Input

输入数据的第1 行有2 个正整数n 和c（n≤10000，c≤10000000），n 表示S 的大小，c是子集和的目标值。接下来的1 行中，有n个正整数，表示集合S中的元素。

Output

将子集和问题的解输出。当问题无解时，输出“No Solution!”。

Samples

Sample #1

Input 

Output 

5 10
2 2 6 5 4

2 2 6

#include
using namespace std;
const int N = 1e4 + 10;
int a[N];
int ans[N] = {0};
int n, c, sum;
bool flag = 0;
void print(int len){
    for(int i = 0; i < len; i++){
        if(i == len - 1){
            cout << ans[i] << "\n";
        }else{
            cout << ans[i] << ' ';
        }
    }
}
void Search(int x, int sum, int len){
    if(sum > c || flag) return ;
    if(sum == c){
        print(len);
        flag = 1;
        return ;
    }
    for(int i = x; i < n; i++){
        if(a[i] + sum <= c){
            ans[len] = a[i];
            Search(i+1, sum+a[i], len+1);
        }
    }
}
int main()
{
    sum = 0;
    cin >> n >> c;
    for(int i = 0; i < n; i++){
        cin >> a[i];
        sum += a[i];
    }
    if(sum < c){
        cout << "No Solution!" << "\n";
    }else{
        Search(0, 0, 0);
        if(!flag){
            cout << "No Solution!" << "\n";
        }
    }
    return 0;
}

B - 运动员最佳匹配问题

Description

羽毛球队有男女运动员各n 人。给定2 个n×n 矩阵P 和Q。P[i][j]是男运动员i 和女运动员j配对组成混合双打的男运动员竞赛优势；Q[i][j]是女运动员i和男运动员j配合的女运动员竞赛优势。由于技术配合和心理状态等各种因素影响，P[i][j]不一定等于Q[j][i]。男运动员i和女运动员j配对组成混合双打的男女双方竞赛优势为P[i][j]*Q[j][i]。
设计一个算法，计算男女运动员最佳配对法，使各组男女双方竞赛优势的总和达到最大。
设计一个算法，对于给定的男女运动员竞赛优势，计算男女运动员最佳配对法，使各组男女双方竞赛优势的总和达到最大。

Input

输入数据的第一行有1 个正整数n (1≤n≤20)。接下来的2n 行，每行n个数。前n行是p，后n行是q。

Output

将计算出的男女双方竞赛优势的总和的最大值输出。

Samples

Sample #1

Input 

Output 

3
10 2 3
2 3 4
3 4 5
2 2 2
3 5 3
4 5 1

52

#include
using namespace std;
const int N = 22;
int n, a[N][N], b[N][N], vis[N], pre[N], sum; 
void dfs(int i, int cnt){
    if(i > n && cnt + pre[n] - pre[i-1] > sum){
        sum = max(sum, cnt);
        return ;
    }
    if(cnt + pre[n] - pre[i-1] > sum){
        for(int j = 1; j <= n; j++){
            if(vis[j] == 0){
                vis[j] = 1;
                dfs(i + 1, cnt + a[i][j] * b[j][i]);
                vis[j] = 0;
            }
        }
    }
}
int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= n; j++){
            cin >> a[i][j];
        }
    }
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= n; j++){
            cin >> b[i][j];
        }
    }
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= n; j++){
            pre[i] = max(pre[i], a[i][j] * b[j][i]);
        }
        pre[i] += pre[i-1];
    }
    dfs(1, 0);
    cout << sum << "\n";
    return 0;
}

C - 工作分配问题

Description

设有n件工作分配给n个人。将工作i分配给第j个人所需的费用为 cij。试设计一个算法，为每一个人都分配1 件不同的工作，并使总费用达到最小。

设计一个算法，对于给定的工作费用，计算最佳工作分配方案，使总费用达到最小。

Input

输入数据的第一行有1 个正整数n (1≤n≤11)。接下来的n行，每行n个数，表示工作费用。

Output

将计算出的最小总费用输出。

Samples

Sample #1

Input 

Output 

3
10 2 3
2 3 4
3 4 5

9

#include
using namespace std;
const int N = 25;
const int INF = 0x3f3f3f3f;
int n, ans;
int a[N][N], vis[N];
void dfs(int i, int sum){
    if(sum > ans) return ;
    if(i == n + 1 && sum < ans){
        ans = sum;
        return ;
    }
    for(int j = 1; j <= n; j++){
        if(!vis[j]){
            vis[j] = 1;
            dfs(i + 1, sum + a[i][j]);
            vis[j] = 0;
        }
    }
}
int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= n; j++){
            cin >> a[i][j];
        }
    }
    ans = INF;
    dfs(1, 0);
    cout << ans << "\n";
    return 0;
}

D - 整数变换问题

Description

整数变换问题。关于整数i的变换f和g定义如下：f(i)=3i；

试设计一个算法，对于给定的2 个整数n和m，用最少的f和g变换次数将n变换为m。例如，可以将整数15用4 次变换将它变换为整数4：4=gfgg(15)。当整数n不可能变换为整数m时，算法应如何处理?
对任意给定的整数n和m，计算将整数n变换为整数m所需要的最少变换次数。

Input

输入数据的第一行有2 个正整数n和m。n≤100000，m≤1000000000。

Output

将计算出的最少变换次数以及相应的变换序列输出。第一行是最少变换次数。第2 行是相应的变换序列。

Samples

Sample #1

Input 

Output 

15 4

4
gfgg

#include
using namespace std;
int maxn, n, m;
char f[101];
int search(int step, int sum){
    if(step > maxn) return 0;
    if(m == sum * 3 || search(step + 1, sum * 3)){
        f[step] = 'f';
        return 1;
    }
    if(sum / 2 == m || search(step+1, sum/2)){
        f[step] = 'g';
        return 1;
    }
    return 0;
}
int main()
{
    cin >> n >> m;
    maxn = 1;
    while(!search(1, n)){
        maxn ++;
    }
    cout << maxn << "\n";
    for(int i = maxn; i >= 1; i--){
        cout << f[i];
    }
    cout << "\n";
    return 0;
}