【Python数据结构与算法】——(线性结构)精选好题分享,不挂科必看系列

时间越小效率越高,所以A的效率高于B,---->选择C

栈的深入理解

2.Suppose 6 items pushed in the relative order like [6,5,4,3,2,1],which pop  order is FALSE?

A.543612

B.453126

C.234156

D.346521

Review Link🔗:👉http://t.csdnimg.cn/LDWaR

进出栈无需一次性进完,一次性弹出.

可以进一个弹一个,也可以进几个,弹几个.

抓住栈的特点,先进后出,有进有出.

​

 ​

​ ​

 只要深入理解栈的知识点,我们通过画图或思考形式就可以做出这道题.

所以这题应该选D,因为5应该比6先出栈.

如何影响链表时间复杂度

3.There is an single Unordered Linked List with two head and rear pointers p and q, respectively. Which of the following operations time complexity that is affected by Linked List lengths
A. Deleting the head.
B. Deleting the rear.
C. Inserting new node to head.
D. Deleting node at rear.

Review Link🔗:👉http://t.csdnimg.cn/ET039 

因为在无序链表中，删除后部需要从头节点开始遍历到尾节点，时间复杂度为O(n)，n为链表长度。而其他操作只需要对头节点进行操作，时间复杂度不受链表长度的影响，几乎为O(1)。---> 选B,D

双端队列的深入理解

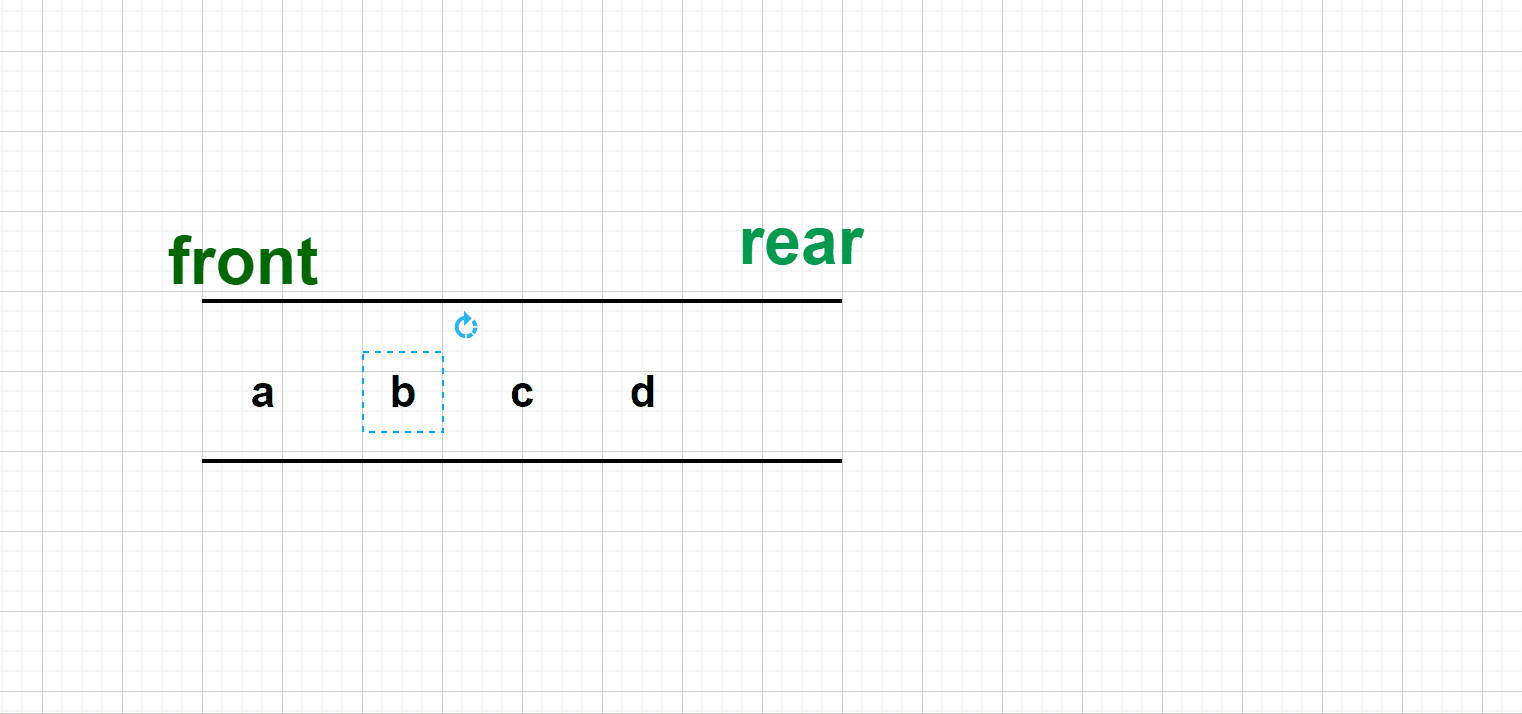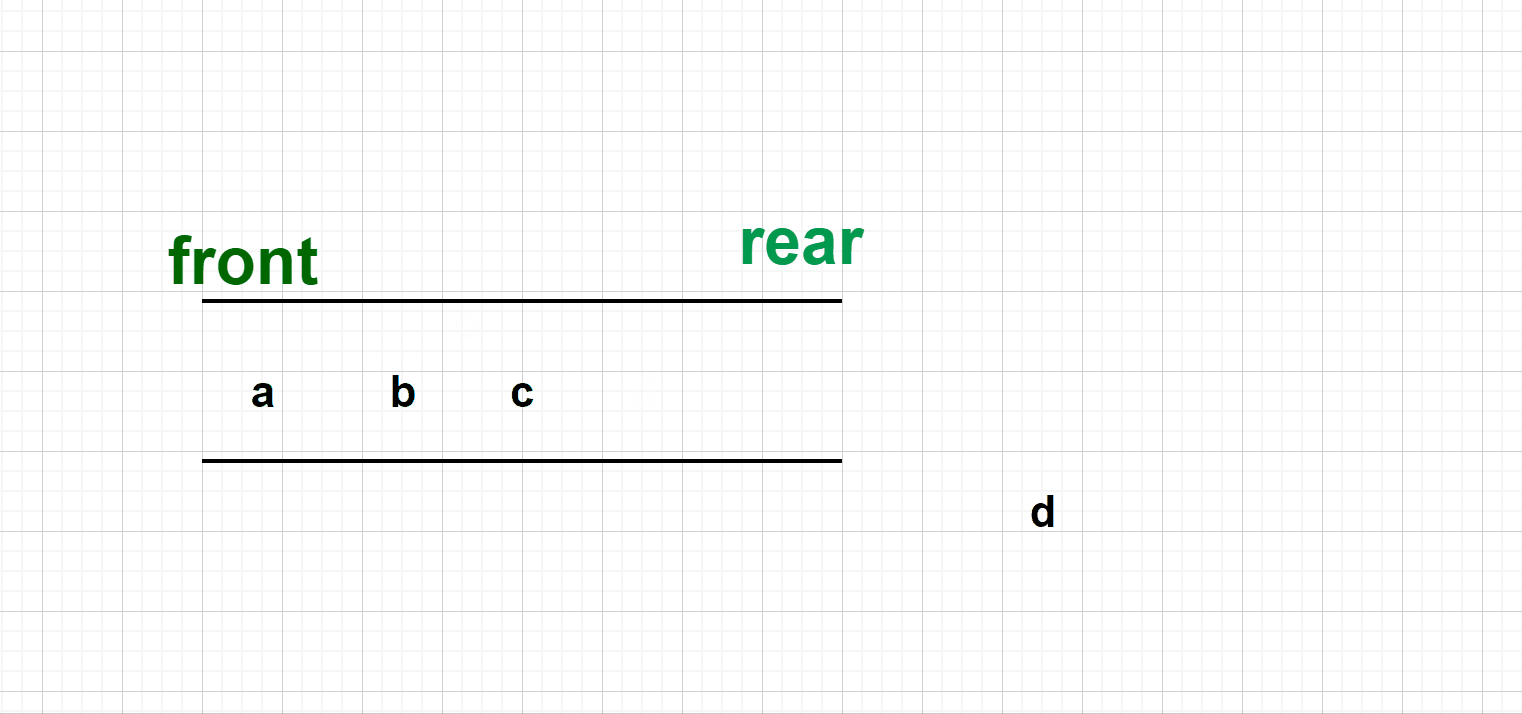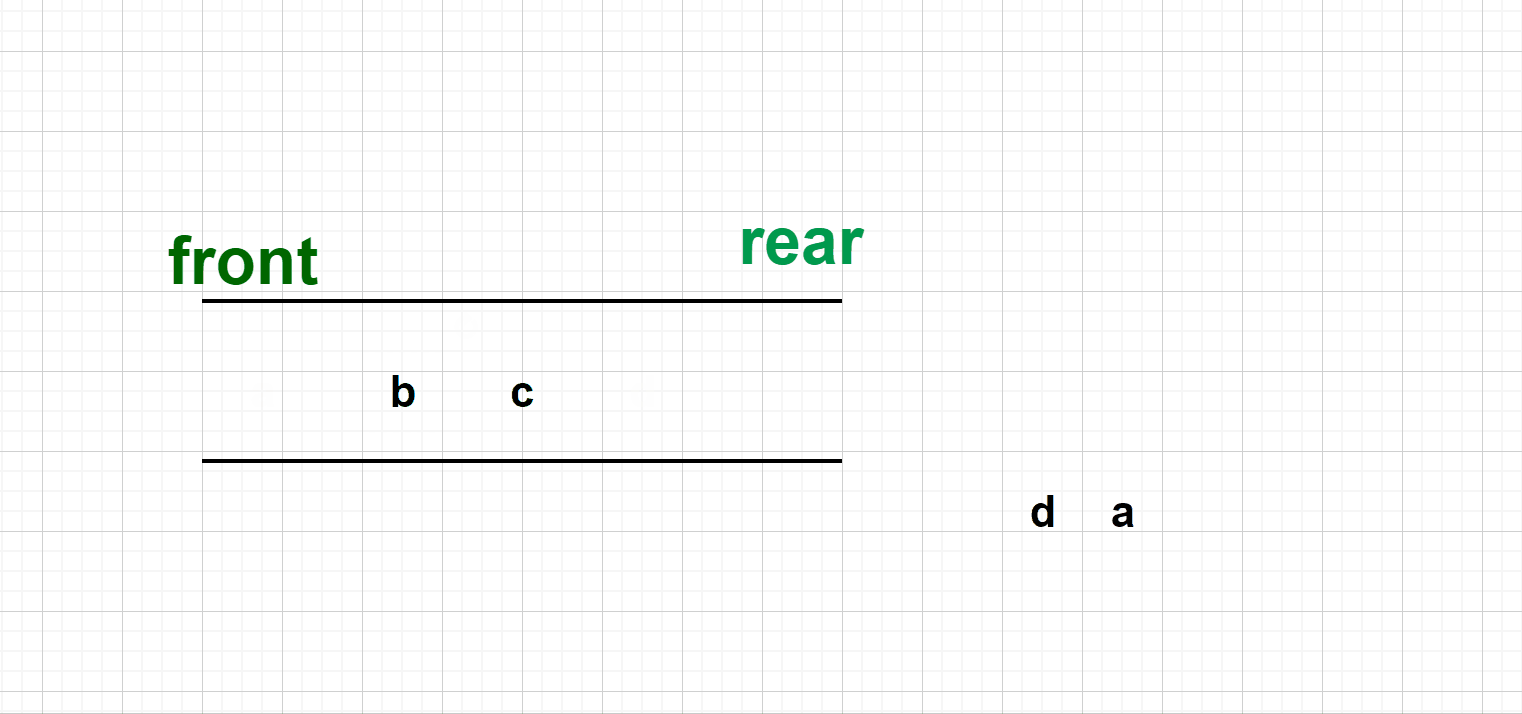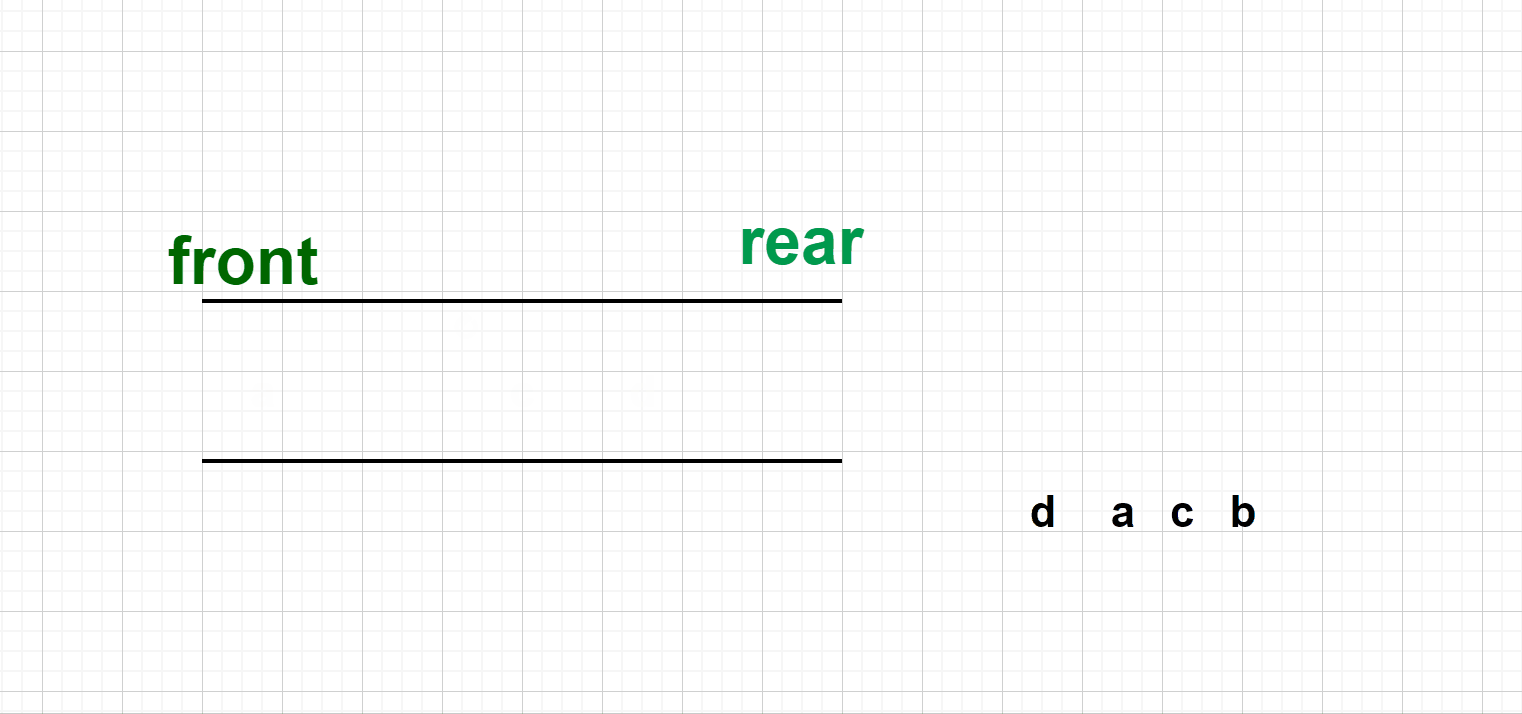
4.Suppose there is enqueue order "abcd' for a Deque (abcd' ehqueued at rear.) What's the possible dequue order for this Deque?
A. bdac
B. cadb
C. dbca
D. dacb
E. None of them is right.

Review Link🔗:👉

双端队列的入队顺序是:abcd,从尾部出,我们知道双端队列的特点就是两头都是可进可出的,但是不可以从中间出去. 所以逐项检验我们可得 ---> D是正确答案

📝Summary:

快速判断算法复杂度(适用于绝大多数简单情况)
确定问题规模n
循环减半过程一logn
k层关于n的循环一n
复杂情况:根据算法执行过程判断

 What's the time complexity of the following code?(n is unknown, n > 10000).

i = 1
if i:
    while i < n:
        i = i * 3
    else:
        while i < n:
            i = i + 10

The time complexity is O(                            ).

该代码的时间复杂度为O(logn)。因为第一个while循环中，i的值每次都会乘以3，直到i>=n为止，每次乘以3相当于对i进行了一次除法运算，假设n=i*3^k，则第一个while循环的迭代次数为log3(n)，即O(logn)。第二个while循环中，i的值每次都会加上10，因此最多执行n/10次，影响可以忽略不计。因此，总的时间复杂度为O(logn)。

 What's the time complexity of the following code ? (n is unknown, n > 10000)

i = 0
j = 0
while i < n:
    i += 1
    while j < n - i:
        j += 1

该代码的时间复杂度为O(n^2)。外循环的执行次数为n，内循环的执行次数为(n-1)+(n-2)+...+1= (n-1)n/2，因此总的执行次数为n(n-1)*0.5，即O(n^2)。

i = 0
j = 0
while i < n:
    i += 1
    while j < n - i:
        j += 1
    j = 0

时间复杂度为O(n^2)。外层循环i最多执行n次，内层循环j最多执行n-i次，因此总的执行次数为n*(n-1)/2，即O(n^2)。

本节主要讲的是算法中如何判断时间复杂度以及深入理解栈,双端队列的特点及应用.若想了解更多关于算法的内容,可以订阅我的算法专栏:http://t.csdnimg.cn/sof15

  今天的干货分享到这里就结束啦！如果觉得文章还可以的话，希望能给个三连支持一下，Aileen的主页还有很多有趣的文章，欢迎小伙伴们前去点评，您的支持就我前进的最大动力！