第五章 树和二叉树（下）【哈夫曼树、并查集】

1. 哈夫曼树

 

1.1 哈夫曼树定义

相关概念：

• 结点的权:有某种现实含义的数值(如:表示结点的重要性等)
• 结点的带权路径长度：从树的根到该结点的路径长度(经过的边数)与该结点上权值的乘积。
• 树的带权路径长度:树中所有叶结点的带权路径长度之和 (WPL,Weighted Path Length)。

哈夫曼树的定义：在含有n个带权叶结点的二叉树中，其中带权路径长度(WPL) 最小的二叉树，也称最优二叉树。

1.2 哈夫曼树的构造（重点）

1.2.1 夫曼树的构造算法

给定n个权值分别为w1, W2,..., w,的结点，构造哈夫曼树的算法描述如下:

1. 将这n个结点分别作为n棵仅含一个结点的二叉树，构成森林F。
2. 构造一个新结点，从F中选取两棵根结点权值最小的树作为新结点的左、右子树（左右顺序任意），并且将新     结点的权值置为左、右子树上根结点的权值之和。
3. 从F中删除刚才选出的两棵树，同时将新得到的树加入F中
4. 重复步骤2和3，直至F中只剩下一棵树为止。
5. 

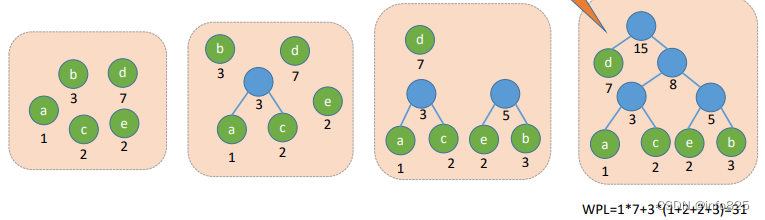
1.2.2 构造哈夫曼树的注意事项：

• 每个初始结点最终都成为叶结点，且权值越小的结点到根结点的路径长度越大
• 哈夫曼树的结点总数为2n - 1
• 哈夫曼树中不存在度为1的结点。
• 哈夫曼树并不唯一，但WPL必然相同且为最优

1.3 哈夫曼编码（重点）

相关概念：

• 固定长度编码：每个字符用相等长度的二进制位表示
• 可变长度编码：允许对不同字符用不等长的二进制位表示
• 若没有一个编码是另一个编码的前缀，则称这样的编码为前缀编码，前缀码解码无歧义

由哈夫曼树得到哈夫曼编码--字符集中的每个字符作为一个叶子结点，各个字符出现的频度作为结点的权值，根据之前介绍的方法构造哈夫曼树 。

哈夫曼树不唯 一，因此哈夫 曼编码不唯一

2. 并查集

 2.1 基本思想

同一子集中的 各个元素，组 织成一棵树，用互不相交的树，表示多个“集合”、

• 如何“查”到一个元素到底属于哪一个集合？—— 从指定元素出发，一路向北，找到根节点
• 如何判断两个元素是否属于同一个集合？—— 分别查到两个元素的根，判断根节点是否相同即可
• 如何把两个集合“并”为一个集合？—— 让一棵树成为另一棵树的子树即可

2.2  “并查集”的存储结构

存储方法为双亲表示法。用一个数组 S[ ] 即可表示“集合”关系

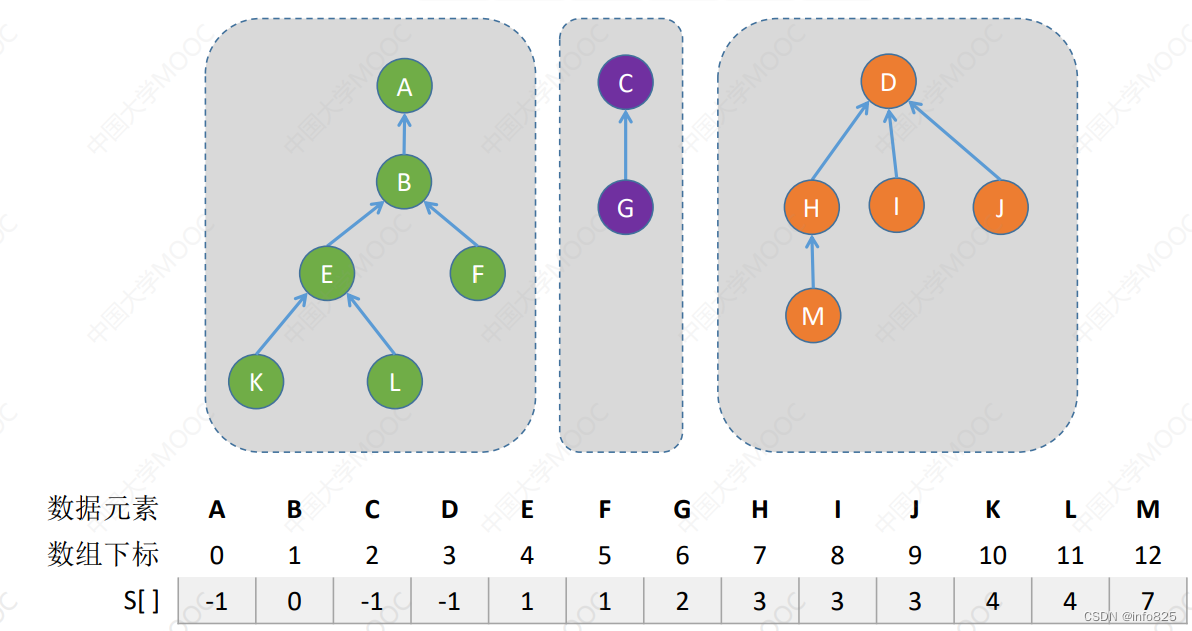
集合的两个基本操作——“并”和“查”

• Find ——“查”操作：确定一个指定元 素所属集合
• Union ——“并”操作：将两个不想交 的集合合并为一个

注：并查集（Disjoint Set）是逻辑结构——集合的一种具体实现，只进行”并”和“查”两种基本操作 

#define SIZE 13
 
int UFSets[SIZE];    //集合元素数组
 
//初始化并查集
void Initial(int S[])
{
    for(int i=0; i
        S[i] = -1;
}
 
//Find————查操作，找到x所属集合    最坏时间复杂度：O(h)
int Find(int S[], int x)
{
    while(S[x]>=0)
    {
        x = S[x];    //循环找x的根
    }
    return x;        // 根的S[]小于0
}
 
//Union————并操作，将两个集合合并   时间复杂度：O(1)  全部合并：O(n^2)
void Union(int S[], int Root1, int Root2)
{
    // 要求Root1和Root2是不同集合
    if(Root1 == Root2)  return;
    // 将root2连接到另一个根Root1下面
    S[Root2] = Root1;
}

 2.3 时间复杂度分析

若结点数为n，Find 最坏时间复杂度为 O(n)，Union时间复杂度 ：O(1)

将n个独立元素通过多次Union合并为一个集合——O(n2)

2.4 优化思路：

2.4.1 Union优化思路

在每次Union操作构建树的时候，尽可能让树不长高高：

①用根节点的负值表示一棵树的结点总数

②Union操作，让小树合并到大树

 合并前：

合并后：

 

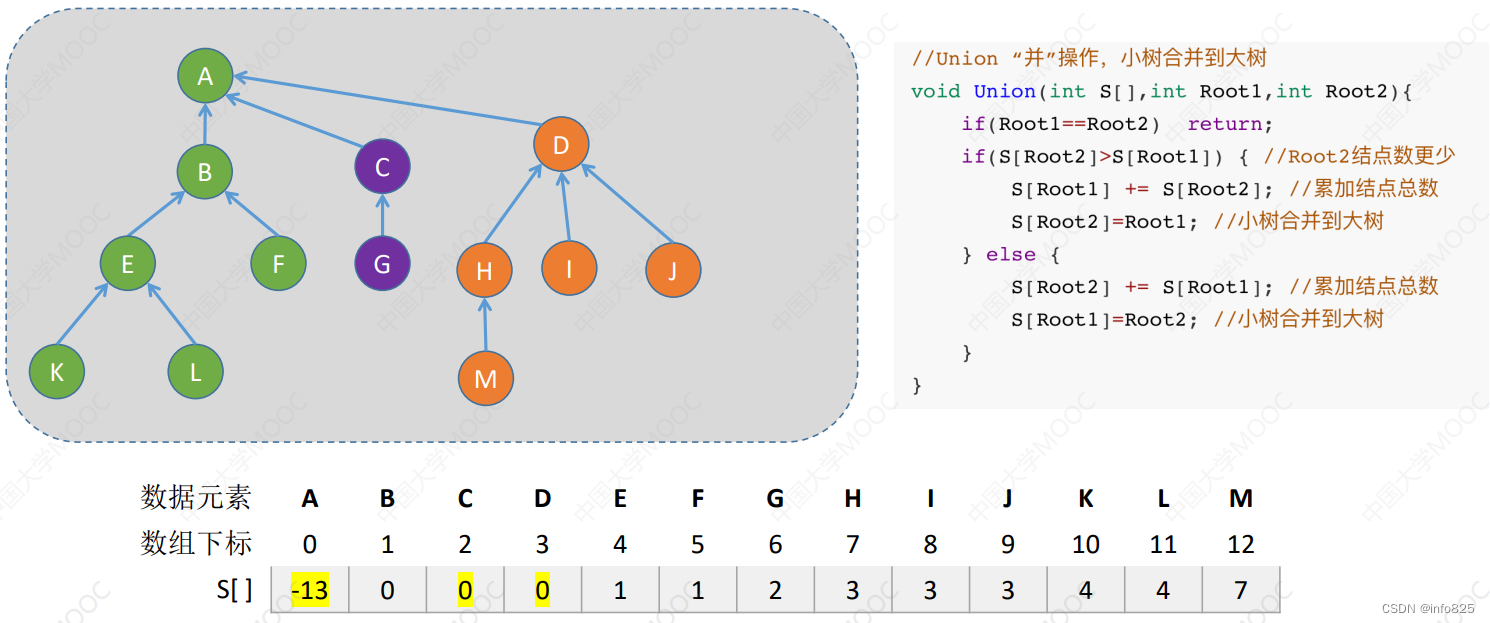
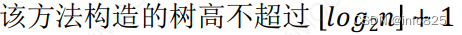
Union操作优化后，Find 操作最坏时间复杂度 ：O(log2n) ,

#define SIZE 13
 
int UFSets[SIZE];    //集合元素数组
 
//初始化并查集
void Initial(int S[])
{
    for(int i=0; i
        S[i] = -1;
}
 
//Find————查操作，找到x所属集合    最坏时间复杂度：O(h)
int Find(int S[], int x)
{
    while(S[x]>=0)
    {
        x = S[x];    //循环找x的根
    }
    return x;        // 根的S[]小于0
}
 
//Union————并操作，将两个集合合并   
void Union(int S[], int Root1, int Root2)
{
    // 要求Root1和Root2是不同集合
    if(Root1 == Root2)  return;
    if (S[Root2]>S[Root1]) {    // Root2结点数更少
        S[Root1] += S[Root2];   // 累加结点总数
        S[Root2] = Root1;       // 小树合并到大树
    } else {
        S[Root2] += S[Root1];   // 累加结点总数
        S[Root1] = Root2;       // 小树合并到大树
    }
}

 2.4.2 Find优化思路：压缩路径，

先找到根节点，再将查找路径上所有节点都挂到根节点下。

每次 Find 操作，先找根，再 “压缩路径”，可使树的高度不超过O(α(n))。 α(n)是一个增长很缓慢
的函数，对于常见的n值，通常α(n)≤4，因此优化后并查集的Find、Union操作时间开销都很低

#define SIZE 13
 
int UFSets[SIZE];    //集合元素数组
 
//初始化并查集
void Initial(int S[])
{
    for(int i=0; i
        S[i] = -1;
}
 
//Find————查操作，找到x所属集合    最坏时间复杂度：O(h)
int Find(int S[], int x)
{
    int root = x;
    while(S[root]>=0) root = S[root];    //循环找x的根
    while(x !=root)
    {
        int t = S[x];    // t指向x的父结点
        S[x] = root;     // x直接挂靠到根节点下面
        x=t;             // 循环处理x的祖先结点
    }
    return x;        // 返回根节点编号
}
 
//Union————并操作，将两个集合合并   
void Union(int S[], int Root1, int Root2)
{
    // 要求Root1和Root2是不同集合
    if(Root1 == Root2)  return;
    if (S[Root2]>S[Root1]) {    // Root2结点数更少
        S[Root1] += S[Root2];   // 累加结点总数
        S[Root2] = Root1;       // 小树合并到大树
    } else {
        S[Root2] += S[Root1];   // 累加结点总数
        S[Root1] = Root2;       // 小树合并到大树
    }
}

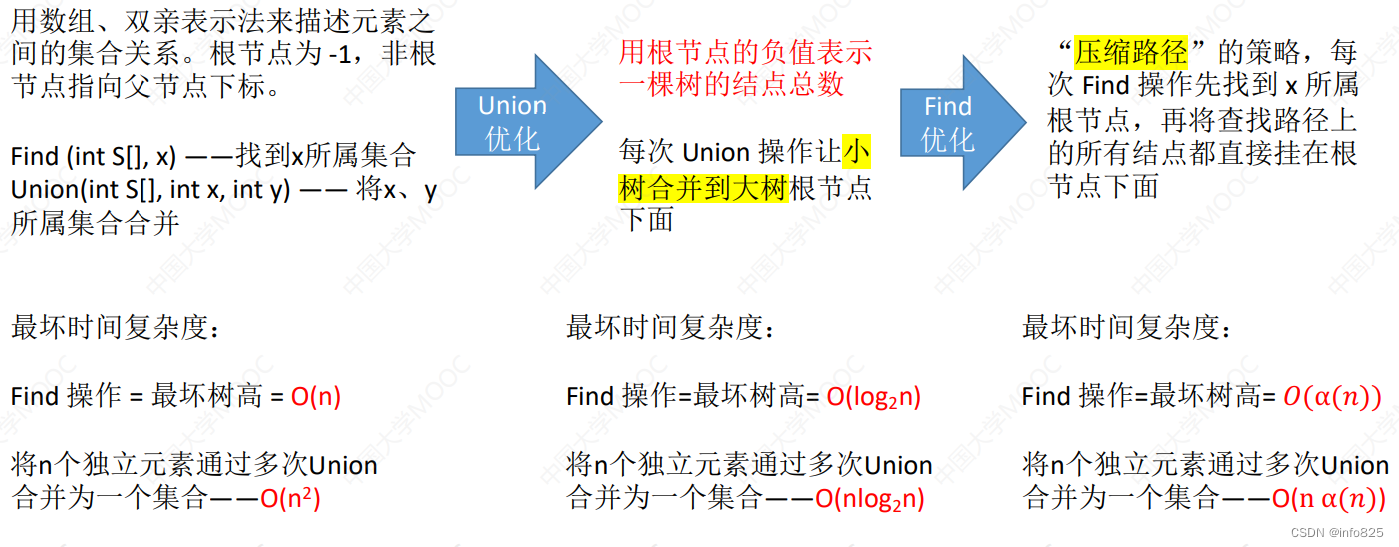
 2.4.3 并查集的优化前后对比