时间序列预测中的4大类8种异常值检测方法(从根源上提高预测精度)

时间序列预测中的4大类8种异常值检测方法(从根源上提高预测精度)
一、本文介绍

本文给大家带来的是时间序列预测中异常值检测，在我们的数据当中有一些异常值（Outliers）是指在数据集中与其他数据点显著不同的数据点。它们可能是一些极端值，与数据集中的大多数数据呈现明显的差异。异常值可能由于测量误差、异常事件、数据收集错误、噪声或其他未知原因而出现。所以因为这些异常值的存在我们的模型不能够很好的识别我们数据的模式，所以我们通常在训练之前都需要处理这些异常值点从而提高模型预测精度，所以就涉及到了本文的内容->异常值检测。本文的内容大家可以配套我的专栏中的实战案例进行使用可以检验你的异常值处理是否有效，

内容回顾：时间序列预测专栏->包括上百种时间序列预测模型、最新顶刊模型复现

目录

一、本文介绍

二、异常值检测方法

三、数据集介绍

三、异常值检测

3.1 基于统计学的方法

3.1.1 标准差的方法

3.1.2 基于箱线图的方法

3.2 基于距离的方法

3.2.1 Z-Score方法

1.2.2 K-NN距离聚类方法

3.3 基于密度的方法

3.3.1 LOF 的离群点检测

3.3.2 DBSCAN

4.4 基于机器学习的方法

4.4.1 孤立森林

4.4.2 自编码器

五、全文总结

二、异常值检测方法

我们选取一些比较常见的方法来介绍，不同的方法适合不同的数据，大家可以都进行尝试再配合自己的经验取判断是否是异常值，从而选取一种适合自己数据的方法，下面是一些方法的简要介绍，后面第三章开始进行讲解。

1. 基于统计学的方法：
- 标准差方法：基于数据的标准差来判断观测值是否与平均值相差较大。
- 箱线图：通过绘制箱线图来显示数据的分布范围和异常值。

2. 基于距离的方法：
- Z-Score 方法：通过计算观测值与平均值之间的差异，标准化数据并将超过某个阈值的值视为异常值。
- K-NN距离聚类方法：使用距离度量来检测与其他数据点距离较远的观测值。

3. 基于密度的方法：
- 基于 LOF 的离群点检测：通过比较每个观测值周围点的密度来识别相对稀有的观测值。
- DBSCAN：根据数据点周围的密度来判断观测值是否为离群点。

4. 基于机器学习的方法：
- 孤立森林：使用随机树构建一种分割方式，将观测值从其他数据点中孤立出来，从而检测异常值。
- 自编码器：通过对正常数据的重构来检测与原始数据重构误差较大的观测值。

这些方法可以根据不同数据集和应用场景的需求进行选择和组合使用。每种方法都有其特定的优势和限制，因此在进行异常值检测时，最好综合考虑多种方法来获得更准确的结果。

请注意：异常值检测并不意味着一定存在异常，它只是用于引起注意并进行进一步的调查。在进行异常值检测时，二一定要根据特定领域的知识和数据背景来确定何种观测值被认为是异常。

三、数据集介绍

本文中我检测异常值用到了两个数据集，一个是官方的ETTh1另一个是某公司的业务水平，前者的官方数据集已经被处理过了数据很平稳，后者的数据集内容里面异常值比较多，所以用这两个数据集来进行一定的对比从而可以让大家更深入的了解异常值检测，下面是两个数据集的部分截图。

三、异常值检测

3.1 基于统计学的方法

3.1.1 标准差的方法

效果评星：⭐

PS：这种方法呢就比较简单就是算均值和方差，超过上界或者下界的就是异常值点，就不多介绍了，均值和方差大家应该都明白。
```
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
 
data = pd.read_csv('ETTh1-Test.csv')
# Calculate the mean and standard deviation
mean = data['OT'].mean()
std_dev = data['OT'].std()
 
# Define the number of standard deviations a data point has to be away from the mean to be considered an outlier
num_std_dev = 2
 
# Find outliers
outliers = data[np.abs(data['OT'] - mean) > num_std_dev * std_dev]
 
# Plotting
plt.figure(figsize=(10, 6))
plt.plot(data['OT'], label='Forecast Data', color='blue', alpha=0.7)
plt.scatter(outliers.index, outliers['OT'], color='red', label='Outliers')
plt.axhline(mean, color='green', linestyle='--', label='Mean')
plt.axhline(mean + num_std_dev * std_dev, color='orange', linestyle='--', label='Upper Bound')
plt.axhline(mean - num_std_dev * std_dev, color='orange', linestyle='--', label='Lower Bound')
 
# Enhancing the plot with a tech-style theme
plt.style.use('ggplot')
plt.title('Forecast Data with Outliers Highlighted', fontsize=15)
plt.xlabel('Index', fontsize=12)
plt.ylabel('Forecast Value', fontsize=12)
plt.legend()
plt.grid(True)
 
# Show the plot
plt.show()
```
3.1.2 基于箱线图的方法

效果评星：⭐⭐⭐

箱线图（Boxplot）确定异常值点的过程通常是基于四分位距来进行的。以下是具体步骤：
1. 计算四分位数：
  
  Q1（第一四分位数）：数据集中所有数值由小到大排列后，位于25%位置的数值。
  Q3（第三四分位数）：同理，位于75%位置的数值。
2. 计算四分位距（IQR）：
  
  IQR = Q3 - Q1
3. 确定异常值范围：
  
  下界（Lower Bound）= Q1 - 1.5 * IQR
  上界（Upper Bound）= Q3 + 1.5 * IQR
4. 判断异常值：
  
  凡是低于下界或高于上界的数值，都被视为异常值。
```
# 完整的代码示例
 
# 导入所需模块
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
 
# 读取数据
file_path = 'new50data (14).csv'
data = pd.read_csv(file_path)
 
# 计算异常值
Q1 = data['forecast'].quantile(0.25)
Q3 = data['forecast'].quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
 
# 标识异常值
data['forecast_Outlier'] = ((data['forecast'] < lower_bound) | (data['forecast'] > upper_bound))
 
# 创建折线图，并在其中标注异常值
plt.figure(figsize=(12, 6))
 
# 绘制OT值的折线图
sns.lineplot(data=data, x=data.index, y='forecast', label='forecast', color='blue')
 
# 标注异常值
outliers = data[data['forecast_Outlier']]
plt.scatter(outliers.index, outliers['forecast'], color='red', label='outlier')
 
plt.style.use('ggplot')
 
# 设置标题和标签
plt.title('forecast outlier detection', fontsize=15)
plt.xlabel('Time', fontsize=12)
plt.ylabel('forecast', fontsize=12)
plt.legend()
 
# 显示图表
plt.show()
 
# 返回异常值的界限和异常值的数量
lower_bound, upper_bound, outliers['OT'].count()
```
3.2 基于距离的方法

3.2.1 Z-Score方法

效果评星：⭐⭐⭐⭐

Z-Score方法，也称为标准分数法，是一种用于识别异常值的统计技术。这种方法通过测量一个数据点与平均值的距离，并将其与标准差相比较来工作。Z-Score是一个表示数据点距离平均数多少个标准差的数值。具体步骤如下：

1. 计算平均值：
- 平均值是所有数据点的总和除以数据点的数量。

2. 计算标准差：
- 标准差是测量数据分布范围的一个统计量，它表示数据点相对于平均值的离散程度。

3. 计算每个数据点的Z-Score：
- 对于每个数据点，Z-Score计算公式为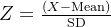： $Z = \frac{(X - \text{Mean})}{\text{SD}}$
- 这里X是单个数据点的值。

4. 确定异常值：
- 异常值通常定义为Z-Score的绝对值大于特定阈值的数据点，常用的阈值是 2 或 3。
- 例如，如果Z-Score的绝对值大于3，那么这个数据点通常被视为异常值。

Z-Score方法在处理具有高斯（正态）分布特征的数据时特别有效。它可以识别那些与大多数数据显著不同的点。然而，对于不是正态分布的数据集，这种方法可能不太适用，因为它依赖于平均值和标准差，这两个参数在非正态分布的数据中可能不会提供有意义的洞察。
```
# 导入所需模块
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
 
# 读取数据
file_path = 'new50data (14).csv'  # 替换为您的文件路径
data = pd.read_csv(file_path)
 
# 计算forecast列的Z分数
data['Forecast_Z_Score'] = stats.zscore(data['forecast'])
 
# 定义离群点（这里以Z分数的绝对值大于2为标准）
data['Forecast_Outlier_Z'] = data['Forecast_Z_Score'].abs() > 2
 
# 创建折线图，并在其中标注离群点
plt.figure(figsize=(12, 6))
plt.style.use('ggplot')
# 绘制forecast值的折线图
sns.lineplot(data=data, x=data.index, y='forecast', label='Forecast Value', color='blue')
 
# 标注离群点
outliers = data[data['Forecast_Outlier_Z']]
plt.scatter(outliers.index, outliers['forecast'], color='red', label='Outliers (Z > 2)')
 
# 设置标题和标签
plt.title('Forecast Value Over Time with Z-Score > 2 Outliers', fontsize=15)
plt.xlabel('Time', fontsize=12)
plt.ylabel('Forecast Value', fontsize=12)
plt.legend()
 
# 显示图表
plt.show()
 
# 返回Z分数大于2的离群点的数量
outliers_count = outliers['forecast'].count()
```
1.2.2 K-NN距离聚类方法

效果评星：这种方法我没测出来，可能是我数据集的原因，不好评价。

使用K-NN算法检测异常值是一种有效的方法，尤其适用于那些需要考虑数据点之间相互关系的场景。K-NN在检测异常值时的基本思想是：如果一个数据点的最近邻（即最接近的K个点）与它相距较远，则该点可能是异常值。下面是K-NN检测异常值的基本步骤：
1. 选择K的值：
  
  确定K的值，即在考虑每个点的邻近点数量。K的值通常较小，如3或5。
2. 计算距离：
  
  对于数据集中的每个点，计算它与所有其他点的距离。
3. 找到最近的K个邻居：
  
  对于每个点，找出距离最近的K个邻居。
4. 确定异常值判定规则：
  
  判定规则可以基于最近邻距离的平均值或最大值。例如，如果一个点与其最近的K个邻居的平均距离远大于大多数点的相应平均距离，则可以将其视为异常值。
5. 标记异常值：
  
  根据上述规则，将那些看似不符合整体数据分布的点标记为异常值。
K-NN方法在检测异常值时的优势在于它不需要假设数据遵循特定的分布，这使得它适用于各种不同类型的数据集。然而，这种方法的效率在高维数据集中可能会降低，因为在高维空间中，计算距离变得复杂且不直观（这被称为“维度的诅咒”大家头一次听说么？）。此外，选择合适的K值也是实现有效检测的关键。

PS：此处需要注意的是我们的数据中都是相邻的点，所以用K-NN没有检测出异常值来。
```
# 设置较小的K值
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.neighbors import NearestNeighbors
import seaborn as sns
file_path = 'new50data (14).csv'  # 替换为你的文件路径
new_data = pd.read_csv(file_path)
 
n_neighbors_smaller = 2  # 减小K值
 
# 使用K-NN模型
knn_smaller = NearestNeighbors(n_neighbors=n_neighbors_smaller)
knn_smaller.fit(new_data[['forecast']])
 
# 计算每个点到其邻居的距离
distances_smaller, _ = knn_smaller.kneighbors(new_data[['forecast']])
 
# 计算平均距离
mean_distance_smaller = np.mean(distances_smaller, axis=1)
 
# 标记离群点
outlier_indices_smaller = np.where(mean_distance_smaller > n_neighbors_smaller)[0]
new_data['Outlier_KNN_Smaller'] = False
new_data.loc[outlier_indices_smaller, 'Outlier_KNN_Smaller'] = True
 
# 重新创建折线图，并在其中标注离群点
plt.figure(figsize=(12, 6))
 
# 绘制forecast值的折线图
sns.lineplot(data=new_data, x=new_data.index, y='forecast', label='Forecast Value', color='blue')
 
# 标注离群点
outliers_knn_smaller = new_data[new_data['Outlier_KNN_Smaller']]
plt.scatter(outliers_knn_smaller.index, outliers_knn_smaller['forecast'], color='red', label='Outliers (KNN, Smaller K)')
 
# 设置标题和标签
plt.title('Forecast Value with KNN Outliers (Smaller K)', fontsize=15, fontweight='bold')
plt.xlabel('Time', fontsize=12)
plt.ylabel('Forecast Value', fontsize=12)
plt.legend()
 
# 显示图表
plt.show()
 
# 返回离群点的数量
outliers_knn_smaller_count = outliers_knn_smaller['forecast'].count()
```
3.3 基于密度的方法

3.3.1 LOF 的离群点检测

效果评星：⭐⭐

LOF（Local Outlier Factor）算法是一种用于检测异常值（离群点）的算法，特别适用于具有高度聚集性质的数据集。它基于一个核心概念：离群点是那些在其邻域内稀疏分布的点。与简单的基于距离的方法不同，LOF考虑了局部密度的概念，从而更有效地识别不同密度区域中的异常值。以下是LOF算法的基本步骤：
1. 计算局部密度：
  
  对于每个点，找出其K个最近邻居（这里的K与K-NN中的K类似，但在LOF中通常称为MinPts）。
  计算每个点到其邻居的距离，这些距离的平均值用来估计该点的局部密度。
2. 计算局部离群因子（LOF）：
  
  对于每个点，比较它的局部密度与其邻居的局部密度。
  LOF分数是该点密度与其邻居密度的比值的平均值。如果一个点的密度远低于其邻居的密度，它的LOF分数将高于1。
3. 标记异常值：
  
  根据LOF分数来判定异常值。通常，分数显著高于1的点被认为是异常值。
LOF算法的优势在于它不仅仅考虑了点之间的距离，而且还考虑了点的局部密度，这使得它在不同密度区域的数据集中表现良好。例如，在一个区域密度高而另一个区域密度低的数据集中，简单基于距离的方法可能会错误地将密度低区域的正常点标记为异常值，而LOF通过考虑局部密度，能够更准确地识别真正的异常值。
```
from sklearn.neighbors import LocalOutlierFactor
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
 
# 重新加载数据
new_file_path = 'new50data (14).csv'
new_data = pd.read_csv(new_file_path)
 
# 设置LoF参数
lof = LocalOutlierFactor(n_neighbors=10)  # 可以调整n_neighbors的值，来调整对数据的敏感度
 
# 使用LoF模型
lof_labels = lof.fit_predict(new_data[['forecast']])
lof_scores = -lof.negative_outlier_factor_  # LoF分数（负数，越小越异常）
 
# 标记离群点
new_data['Outlier_LoF'] = (lof_labels == -1)
 
# 创建折线图，并在其中标注离群点
plt.figure(figsize=(12, 6))
 
# 使用科技感的样式
sns.set(style="whitegrid")
 
# 绘制forecast值的折线图
sns.lineplot(data=new_data, x=new_data.index, y='forecast', label='Forecast Value', color='blue')
 
# 标注离群点
outliers_lof = new_data[new_data['Outlier_LoF']]
plt.scatter(outliers_lof.index, outliers_lof['forecast'], color='red', label='Outliers (LoF)')
 
# 设置标题和标签
plt.title('Forecast Value with LoF Outliers', fontsize=15, fontweight='bold')
plt.xlabel('Time', fontsize=12)
plt.ylabel('Forecast Value', fontsize=12)
plt.legend()
 
# 显示图表
plt.show()
 
# 返回离群点的数量
outliers_lof_count = outliers_lof['forecast'].count()
outliers_lof_count
```
3.3.2 DBSCAN

效果评星：⭐⭐⭐⭐⭐

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，用于将数据集中紧密相连的点组成簇，同时识别并排除异常值（噪声）。与基于距离或假设特定分布的聚类算法不同，DBSCAN专注于基于密度的聚类，这使得它可以识别任何形状的聚类，同时对异常值具有较好的鲁棒性。DBSCAN的基本原理和步骤如下：
1. 核心概念：
  
  核心点：在给定半径（Eps）内有足够多（MinPts）邻居的点。
  边界点：在核心点的Eps邻域内但自身不满足核心点条件的点。
  噪声点：既不是核心点也不是边界点的点。
2. 基本步骤：
  
  参数设定：确定两个关键参数——Eps（邻域半径）和MinPts（邻域内要求的最少点数）。
  识别核心点：对于每个点，如果其Eps邻域内有至少MinPts个点，则该点被标记为核心点。
  形成聚类：对于每个核心点，如果它尚未被分配到任何聚类中，开始创建一个新的聚类。然后，将所有与该核心点直接密集可达的点（包括其他核心点和边界点）添加到该聚类中。
  处理边界点：边界点可能被多个核心点共享，但它们会被分配到其中一个核心点所在的聚类。
  标识噪声：所有既不是核心点也不是边界点的点被视为噪声。
3. 结果：
  
  最终，DBSCAN生成的聚类可能具有任意形状，算法还会识别并排除数据集中的噪声点。
DBSCAN的优点包括它不需要事先知道聚类的数量，能处理任意形状的聚类，并且对噪声具有较强的鲁棒性。然而，选择合适的Eps和MinPts参数对于获得好的聚类结果非常关键。特别是在数据集的密度不均匀时，选择一个全局最优的Eps和MinPts可能比较困难。此外，DBSCAN的性能在处理大规模高维数据时可能会下降，因为在高维空间中，所有点之间的距离都倾向于变得相似（这也是所谓的“维度的诅咒”）。
```
import pandas as pd
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt
import seaborn as sns
 
new_file_path = 'ETTh1-Test.csv'
new_data = pd.read_csv(new_file_path)
# 设置DBSCAN参数
dbscan = DBSCAN(eps=0.05, min_samples=5)  # 参数可能需要根据数据进行调整
 
# 使用DBSCAN模型
dbscan_labels = dbscan.fit_predict(new_data[['OT']])
 
# 标记离群点（在DBSCAN中，-1标签表示离群点）
new_data['Outlier_DBSCAN'] = (dbscan_labels == -1)
 
# 创建折线图，并在其中标注离群点
plt.figure(figsize=(12, 6))
 
# 绘制forecast值的折线图
sns.lineplot(data=new_data, x=new_data.index, y='OT', label='OT Value', color='blue')
 
# 标注离群点
outliers_dbscan = new_data[new_data['Outlier_DBSCAN']]
plt.scatter(outliers_dbscan.index, outliers_dbscan['OT'], color='red', label='Outliers (DBSCAN)')
 
# 设置标题和标签
plt.title('OT Value with DBSCAN Outliers', fontsize=15, fontweight='bold')
plt.xlabel('Time', fontsize=12)
plt.ylabel('Forecast Value', fontsize=12)
plt.legend()
 
# 显示图表
plt.show()
 
# 返回离群点的数量
outliers_dbscan_count = outliers_dbscan['forecast'].count()
```
4.4 基于机器学习的方法

4.4.1 孤立森林

效果评星：⭐⭐⭐

孤立森林（Isolation Forest）是一种有效的异常值检测算法，特别适用于高维数据集。它基于这样一个简单的原理：异常值通常是稀有的并且与大多数其他数据点有显著的不同，因此更容易被“孤立”。下面是孤立森林算法的基本步骤和原理：
1. 随机抽样：
  
  从数据集中随机抽取一定数量的样本。这些样本被用来构建孤立树（Isolation Trees）。
2. 构建孤立树：
  
  对于每棵树，算法随机选择一个特征并随机选择一个分割值。基于这个特征和分割值，数据集被分割成两部分。这个过程递归进行，直到每个数据点都被“孤立”（即每个点都成为了树中的一个叶子节点）或达到了预设的树深度限制。
3. 路径长度：
  
  在每棵孤立树中，每个点的路径长度被记录下来。路径长度是指从树的根节点到达该点所经过的边的数量。异常值由于更容易被孤立，通常会有更短的路径长度。
4. 计算异常得分：
  
  通过对一个点在多棵孤立树中的路径长度进行平均，可以计算出该点的异常得分。得分越高，该点越可能是异常值。
5. 判断异常值：
  
  根据设定的阈值或者通过比较所有点的异常得分，可以判定哪些点是异常值。
孤立森林的主要优点在于它对于大数据集和高维数据的高效处理能力，以及不需要基于任何分布假设。它特别适合于处理连续型数据。此外，由于其随机和递归的特性，孤立森林对于数据集中的小的异常群体也很敏感。
```
from sklearn.ensemble import IsolationForest
import pandas as pd
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt
import seaborn as sns
 
new_file_path = 'new50data (14).csv'
new_data = pd.read_csv(new_file_path)
# 设置孤立森林参数
iso_forest = IsolationForest(n_estimators=100, contamination='auto', random_state=42)  # 可调整参数
 
# 使用孤立森林模型
iso_labels = iso_forest.fit_predict(new_data[['forecast']])
 
# 标记离群点（在孤立森林中，-1标签表示离群点）
new_data['Outlier_IsolationForest'] = (iso_labels == -1)
 
# 创建折线图，并在其中标注离群点
plt.figure(figsize=(12, 6))
 
# 绘制forecast值的折线图
sns.lineplot(data=new_data, x=new_data.index, y='forecast', label='Forecast Value', color='blue')
 
# 标注离群点
outliers_iso_forest = new_data[new_data['Outlier_IsolationForest']]
plt.scatter(outliers_iso_forest.index, outliers_iso_forest['forecast'], color='red', label='Outliers (Isolation Forest)')
 
# 设置标题和标签
plt.title('Forecast Value with Isolation Forest Outliers', fontsize=15, fontweight='bold')
plt.xlabel('Time', fontsize=12)
plt.ylabel('Forecast Value', fontsize=12)
plt.legend()
 
# 显示图表
plt.show()
 
# 返回离群点的数量
outliers_iso_forest_count = outliers_iso_forest['forecast'].count()
outliers_iso_forest_count
```
4.4.2 自编码器

效果评星：⭐⭐⭐⭐⭐

自编码器（Autoencoder）是一种基于神经网络的算法，通常用于数据的降维和特征学习。由于其能力在于学习数据的正常分布，自编码器也被用于异常值检测。在这种应用中，自编码器通过学习重构正常数据的特征，然后利用重构误差来识别异常值。以下是使用自编码器进行异常值检测的基本步骤：
1. 自编码器结构：
  
  自编码器通常包括两部分：编码器（Encoder）和解码器（Decoder）。
  编码器将输入数据压缩成一个低维表示（称为编码）。
  解码器从这个低维表示重构原始输入数据。
2. 训练自编码器：
  
  使用正常数据（没有异常值的数据）训练自编码器。
  训练的目标是最小化输入数据和重构数据之间的差异，通常使用均方误差作为损失函数。
3. 计算重构误差：
  
  在训练完成后，用自编码器对新的数据进行编码和解码。
  计算每个数据点的重构误差，即输入数据和重构数据之间的差异。
4. 异常值判定：
  
  基于重构误差来判定数据是否异常。
  如果一个数据点的重构误差显著高于大多数其他数据点的误差，那么它可能是一个异常值。
自编码器在异常值检测中的优点包括其对数据特征的非线性和复杂关系的捕捉能力。这使得它适合于处理复杂的数据集。此外，由于是基于重构误差进行异常检测，自编码器不需要异常值的标签。
```
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import os
os.environ['KMP_DUPLICATE_LIB_OK']='TRUE'
# 加载数据
data_path = 'new50data (14).csv'  # 替换为您的文件路径
new_data = pd.read_csv(data_path)
 
# 准备数据
data_tensor = torch.tensor(new_data['forecast'].values.astype(np.float32)).view(-1, 1)
dataset = TensorDataset(data_tensor, data_tensor)
dataloader = DataLoader(dataset, batch_size=32, shuffle=True)
 
# 定义自编码器模型
class Autoencoder(nn.Module):
    def __init__(self):
        super(Autoencoder, self).__init__()
        self.encoder = nn.Sequential(
            nn.Linear(1, 2),
            nn.ReLU())
        self.decoder = nn.Sequential(
            nn.Linear(2, 1),
            nn.Sigmoid())
 
    def forward(self, x):
        x = self.encoder(x)
        x = self.decoder(x)
        return x
 
# 初始化模型、损失函数和优化器
model = Autoencoder()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
 
# 训练模型
num_epochs = 50
for epoch in range(num_epochs):
    for data in dataloader:
        inputs, _ = data
        outputs = model(inputs)
        loss = criterion(outputs, inputs)
 
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
 
# 评估模型
model.eval()
with torch.no_grad():
    predictions = model(data_tensor)
    mse = nn.functional.mse_loss(predictions, data_tensor, reduction='none')
    mse = mse.view(-1).numpy()
 
new_data['Reconstruction_Error'] = mse
 
# 定义重建误差的阈值为离群点
threshold = np.percentile(new_data['Reconstruction_Error'], 95)
new_data['Outlier_Autoencoder'] = new_data['Reconstruction_Error'] > threshold
 
# 使用seaborn样式
sns.set(style="whitegrid")
 
# 创建折线图，并在其中标注离群点
plt.figure(figsize=(12, 6))
 
# 绘制forecast值的折线图
plt.plot(new_data['forecast'], label='Forecast Value', color='blue')
 
# 标注离群点
outliers = new_data[new_data['Outlier_Autoencoder']]
plt.scatter(outliers.index, outliers['forecast'], color='red', label='Outliers (Autoencoder)')
 
# 设置标题和标签
plt.title('Forecast Value with Autoencoder Outliers', fontsize=15, fontweight='bold')
plt.xlabel('Time', fontsize=12)
plt.ylabel('Forecast Value', fontsize=12)
plt.legend()
 
# 显示图表
plt.show()
```
五、全文总结

到此本文的异常值检测方法就全部讲完了，当然还有其它的异常值检测方法，但是上面几种是最常见的，其它的要么就太复杂，要么就比较老了，就不讲了，大家有兴趣可以自己调查调查，本文的内容是为了配合我的专栏进行数据预处理的操作，下一个文章我会发布当我们检测到异常值之后，对异常值处理的方法，下面推荐我的专栏内容给大家~

概念理解

15种时间序列预测方法总结(包含多种方法代码实现)

数据分析

时间序列预测中的数据分析-＞周期性、相关性、滞后性、趋势性、离群值等特性的分析方法

机器学习——难度等级(⭐⭐)

时间序列预测实战(四)(Xgboost)(Python)(机器学习)图解机制原理实现时间序列预测和分类(附一键运行代码资源下载和代码讲解)

深度学习——难度等级(⭐⭐⭐⭐)

时间序列预测实战(五)基于Bi-LSTM横向搭配LSTM进行回归问题解决

时间序列预测实战(七)(TPA-LSTM)结合TPA注意力机制的LSTM实现多元预测

时间序列预测实战(三)(LSTM)(Python)(深度学习)时间序列预测(包括运行代码以及代码讲解)

时间序列预测实战(十一)用SCINet实现滚动预测功能(附代码+数据集+原理介绍）

时间序列预测实战(十二)DLinear模型实现滚动长期预测并可视化预测结果

时间序列预测实战(十五)PyTorch实现GRU模型长期预测并可视化结果

Transformer——难度等级(⭐⭐⭐⭐)

时间序列预测模型实战案例(八)(Informer)个人数据集、详细参数、代码实战讲解

时间序列预测模型实战案例(一)深度学习华为MTS-Mixers模型

时间序列预测实战(十三)定制化数据集FNet模型实现滚动长期预测并可视化结果

时间序列预测实战(十四)Transformer模型实现长期预测并可视化结果（附代码+数据集+原理介绍）

个人创新模型——难度等级(⭐⭐⭐⭐⭐)

时间序列预测实战(十)(CNN-GRU-LSTM)通过堆叠CNN、GRU、LSTM实现多元预测和单元预测

传统的时间序列预测模型(⭐⭐)

时间序列预测实战(二)(Holt-Winter)(Python)结合K-折交叉验证进行时间序列预测实现企业级预测精度(包括运行代码以及代码讲解)

时间序列预测实战(六)深入理解ARIMA包括差分和相关性分析

融合模型——难度等级(⭐⭐⭐)

时间序列预测实战(九)PyTorch实现融合移动平均和LSTM-ARIMA进行长期预测

时间序列预测实战(十六)PyTorch实现GRU-FCN模型长期预测并可视化结果
相关阅读:
Python------学生管理（文件txt处理）
数据结构与算法复习：第三十二弹
 2.docker镜像的导入导出
 web框架之路由列表及SQL语句查询数据库数据替换模板变量
 经常散步好不好？60以上老人3个好处收入囊中，但有3点要注意
 全球线栅偏振片（WGP）市场规模分析及发展预测
 gcexcel-java-5.2.5 Crack update in 2022-11-28
[ExRandom lib-examples]
如何利用ChatGPT提升学术论文写作效率
 售卖机控制板开发，轻松实现线下售卖和线上运营
原文地址：https://blog.csdn.net/java1314777/article/details/134456199

一、本文介绍

二、异常值检测方法

三、数据集介绍

三、异常值检测

3.1 基于统计学的方法

3.1.1 标准差的方法

3.1.2 基于箱线图的方法

3.2 基于距离的方法

3.2.1 Z-Score方法

1.2.2 K-NN距离聚类方法

3.3 基于密度的方法

3.3.1 LOF 的离群点检测

3.3.2 DBSCAN

4.4 基于机器学习的方法

4.4.1 孤立森林

4.4.2 自编码器

五、全文总结