-
【机器学习9】前馈神经网络
深度前馈网络是一类网络模型的统称,主要包括多层感知机、 自编码器、限制玻尔兹曼机, 以及卷积神经网络等。
1 激活函数
激活函数及对应导函数 图 其它 Sigmoid 

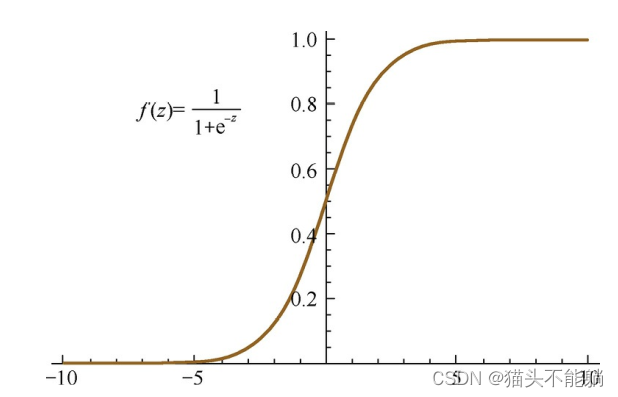
导数 在z很大或很小时都会趋近于0, 造成梯度消失的现象 Tanh 

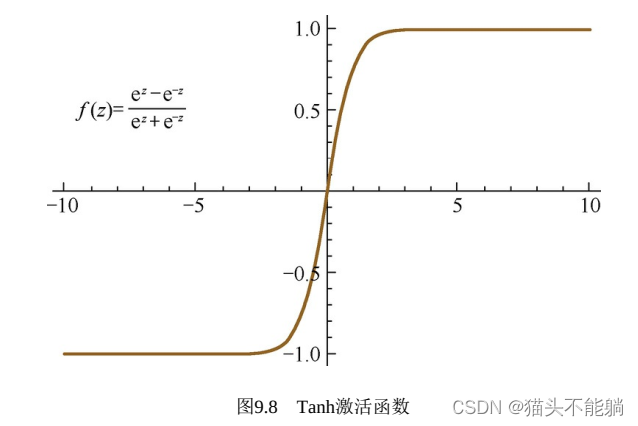
其导数在z很大或很小时都会趋近于0, 同样会出现“梯度消失 ReLU 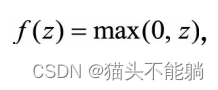

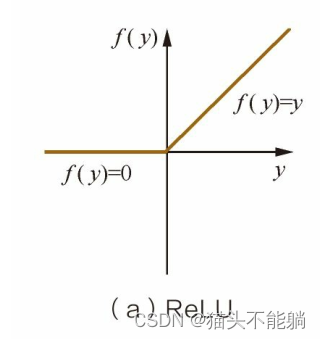
ReLU只需要一个阈值即可得到激活值,有效地解决梯度消失的问题,单侧抑制提供了网络的稀疏表达能力。局限性在于其训练过程中会导致神经元死亡的问题 :负梯度在经过该ReLU单元时被置为0, 且在之后也不被任何数据激活, 即流经该神经元的梯度永远为0, 不对任何数据产生响应。 LReLU 
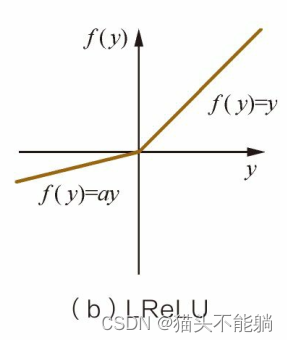
既实现了单侧抑制, 又保留了部分负梯度信息以致不完全丢失。但a值的选择增加了问题难度, 需要较强的人工先验或多次重复训练以确定合适的参数值 PReLU 与LReLU的主要区别是将负轴部分斜率a作为网络中一个可学习的参数, 进行反向传播训练, 与其他含参数网络层联合优化。 2 多层感知机
2.1 网络结构
定义第(l)层的输入为x(l), 输出为a(l); 在每一层中, 首先利用输入x(l)和偏置b(l)计算仿射变换z(l)=W(l)x(l)+b(l); 然后激活函数f作用于z(l), a(l)直接作为下一层的输入, 即x(l+1)。
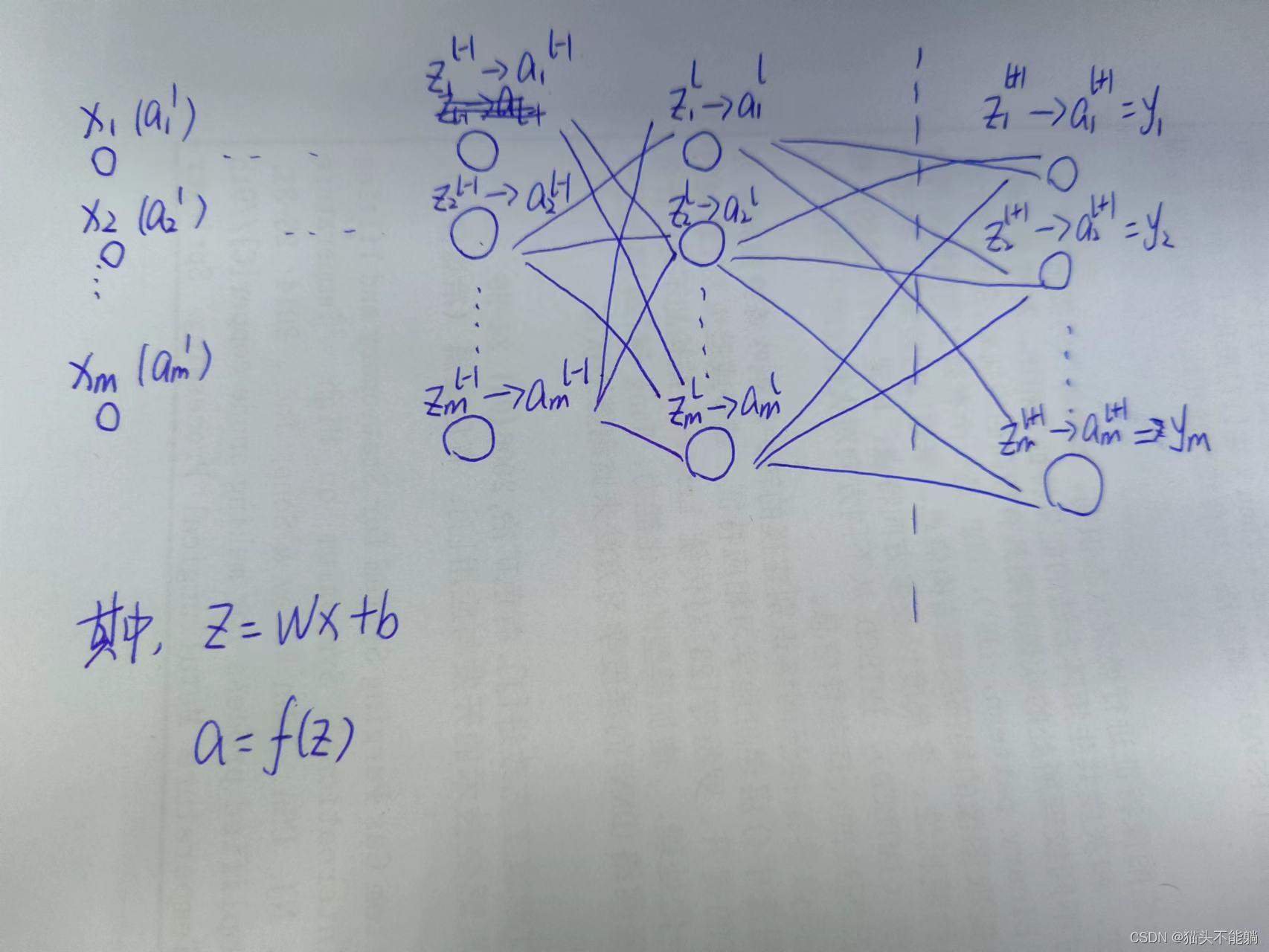
在网络训练中, 前向传播最终产生一个标量损失函数, 反向传播算法(BackPropagation) 则将损失函数的信息沿网络层向后传播用以计算梯度, 达到优化网络参数的目的。2.2 平方误差和交叉熵损失函数
给定包含m样本的集合 , 其整体代价函数为:
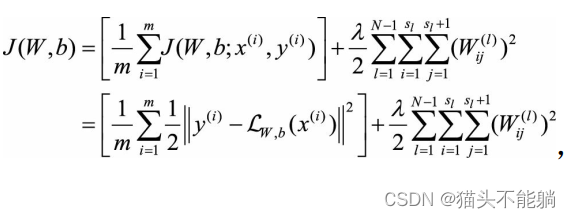
其中第一项为平方误差项, 第二项为L2正则化项。
梯度下降法中每次迭代对参数W(网络连接权重) 和b(偏置) 进行更新:

 下面针对两种不同的损失函数计算最后一层的残差δ(L); 得到δ(L)之后, 其他层的残差δ(L−1),…, δ(1)可以根据上面得到的递推公式计算。 进行简化计算,重点关注梯度产生的损失:
下面针对两种不同的损失函数计算最后一层的残差δ(L); 得到δ(L)之后, 其他层的残差δ(L−1),…, δ(1)可以根据上面得到的递推公式计算。 进行简化计算,重点关注梯度产生的损失:
平方损失函数更适合输出为连续, 并且最后一层不含Sigmoid或Softmax激活函数的神经网络; 交叉熵损失则更适合二分类或多分类的场景。
3 Dropout和批量归一化
3.1Dropout
要求某个神经元节点激活值以一定的概率p被“丢弃”,即该神经元暂时停止工作。对于任意神经元, 每次训练中都与一组随机挑选的不同的神经元集合共同进行优化, 这个过程会减弱全体神经元之间的联合适应性, 减少过拟合的风险, 增强泛化能力。

3.2批量归一化
神经网络训练过程的本质是学习数据分布, 如果训练数据与测试数据的分布不同将大大降低网络的泛化能力, 因此我们需要在训练开始前对所有输入数据进行归一化处理。批量归一化方法是针对每一批数据, 在网络的每一层输入之前增加归一化处理(均值为0, 标准差为1)
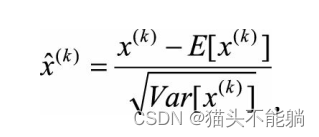
其中x(k)为该层第k个神经元的原始输入数据, E[x(k)]为这一批输入数据在第k个神经元的均值, 为这一批数据在第k个神经元的标准差。
为这一批数据在第k个神经元的标准差。
批量归一化可以看作在每一层输入和上一层输出之间加入了一个新的计算层, 对数据的分布进行额外的约束, 从而增强模型的泛化能力。 但是批量归一化同时也降低了模型的拟合能力, 归一化之后的输入分布被强制为0均值和1标准差。 为了恢复原始数据分布, 具体实现中引入了变换重构以及可学习参数γ和β:

其中γ(k)和β(k)分别为输入数据分布的方差和偏差。在批量归一化操作中, γ和β变成了该层的学习参数, 仅用两个参数就可以恢复最优的输入数据分布, 与之前网络层的参数解耦, 从而更加有利于优化的过程, 提高模型的泛化能力。4深度卷积神经网络
卷积神经网络特点是每层的神经元节点只响应前一层局部区域范围内的神经元。
深度卷积神经网络模型通常由若干卷积层叠加若干全连接层组成, 中间也包含各种非线性操作以及池化操作。
由于卷积运算主要用于处理类网格结构的数据, 因此对于时间序列以及图像数据的分析与识别具有显著优势。
卷积操作的本质特性包括稀疏交互和参数共享。4.1 稀疏交互
卷积核尺度远小于输入的维度, 这样每个输出神经元仅与前一层特定局部区域内的神经元存在连接权重(即产生交互) , 我们称这种特性为稀疏交互, 假设网络中相邻两层分别具有m个输入和n个输出, 全连接网络中的权值参数矩阵将包含m×n个参数。 对于稀疏交互的卷积网络, 如果限定每个输出与前一层神经元的连接数为k, 那么该层的参数总量为k×n。


稀疏交互的物理意义是, 通常图像、 文本、 语音等现实世界中的数据都具有局部的特征结构, 我们可以先学习局部的特征, 再将局部的特征组合起来形成更复杂和抽象的特征。 以人脸识别为例, 最底层的神经元可以检测出各个角度的边缘特征 ; 位于中间层的神经元可以将边缘组合起来得到眼睛、鼻子、 嘴巴等复杂特征 ; 最后, 位于上层的神经元可以根据各个器官的组合检测出人脸的特征 。
4.2 参数共享
参数共享是指在同一个模型的不同模块中使用相同的参数, 它是卷积运算的固有属性。
全连接网络中, 计算每层的输出时, 权值参数矩阵中的每个元素只作用于某个输入元素一次; 而在卷积神经网络中, 卷积核中的每一个元素将作用于每一次局部输入的特定位置上。 根据参数共享的思想, 我们只需要学习一组参数集合, 而不需要针对每个位置的每个参数都进行优化。4.3 池化
池化操作的本质是降采样。 池化操作除了能显著降低参数量外, 还能够保持对平移、 伸缩、 旋转操作的不变性。
原理 特点 均值池化 通过对邻域内特征数值求平均来实现, 能够抑制由于邻域大小受限造成估计值方差增大的现象 对背景的保留效果更好 最大池化 通过取邻域内特征的最大值来实现, 能够抑制网络参数误差造成估计均值偏移的现象 更好地提取纹理信息 相邻重叠区域的池化 采用比窗口宽度更小的步长, 使得窗口在每次滑动时存在重叠的区域 空间金字塔池化 主要考虑了多尺度信息的描述, 例如同时计算1×1、 2×2、 4×4的矩阵的池化并将结果拼接在一起作为下一网络层的输入 5深度残差网络
5.1 梯度消失
在2.2中推导的误差传播公式为:
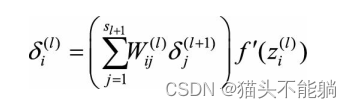
如果再展开所有层的话,就涉及很多参数以及导数的连乘,这时误差很容易产生消失或者膨胀, 影响对该层参数的正确学习。 因此深度神经网络的拟合和泛化能力较差, 有时甚至不如浅层的神经网络模型精度更高。

ResNet把网络结构调整为, 既然离输入近的神经网络层较难训练, 那么我们可以将它短接到更靠近输出的层,输入x经过两个神经网络的变换得到F(x), 同时也短接到两层之后, 最后这个包含两层的神经网络模块输出H(x)=F(x)+x。
-
相关阅读:
公寓报修系统(IDEA,SSM,MySQL)
Flutter Fair逻辑动态化架构设计与实现
【数据结构】查找——散列表(哈希表小总结 附例题)
Spring Security(十八)--OAuth2:实现授权服务器(上)--环境准备以及骨架代码搭建
TCP/IP模型原理(理论)
【2024秋招】万得后端开发java 2023-7-13 2.30pm 一二面面经(附答案)
P21升级后,用旧的spec模板生成的defime.xml中WhereClauses(VLM)里的逗号不能正常显示
企业架构LNMP学习笔记33
macOS Sonoma 14.2beta2(23C5041e)发布(附黑白苹果镜像地址)
spring-data-redis操作redis集群出现的错误
- 原文地址:https://blog.csdn.net/aimaimaim/article/details/134440499