图像相似度对比方法

1.哈希方法，其中包括均值哈希、插值哈希、感知哈希方法。计算出图片的哈希值，一般使用汉明

距离计算两个图片间的差距。

2.直方图算法，其中包括灰度直方图算法，RGB直方图算法，

3.灰度图算法：MSE、SSIM、图像相似度算法

4.余弦相似性、欧氏距离

5.MD5

一、直方图算法

方法描述：按照某种距离度量的标准对两幅图像的直方图进行相似度的测量。

• 优点：计算量比较小。
• 缺点： 直方图反应的是图像灰度值得概率分布，并没有图像的空间位置信息在里面，因此，会出现误判；比如纹理结构相同，但明暗不同的图像，应该相似度很高，但实际结果是相似度很低，而纹理结构不同，但明暗相近的图像，相似度却很高。

分析：两幅图像之间的距离度量，采用的是巴氏距离或者归一化相关系数，这种用分析数学向量的方法去分析图像本身就是一个很不好的办法。

（1）单通道直方图

def histogram(image1, image2):
        # 灰度直方图算法
        # 计算单通道的直方图的相似值
        hist1 = cv2.calcHist([image1], [0], None, [256], [0.0, 255.0])
        hist2 = cv2.calcHist([image2], [0], None, [256], [0.0, 255.0])
        # 计算直方图的重合度
        degree = 0
        for i in range(len(hist1)):
            if hist1[i] != hist2[i]:
                degree = degree + \
                         (1 - abs(hist1[i] - hist2[i]) / max(hist1[i], hist2[i]))
            else:
                degree = degree + 1
        degree = degree / len(hist1)
        return degree

（2）RGB三通道直方图

def Multiparty_histogram(self, image1, image2, size=(256, 256)):
        # RGB每个通道的直方图相似度
        # 将图像resize后，分离为RGB三个通道，再计算每个通道的相似值
        image1 = cv2.resize(image1, size)
        image2 = cv2.resize(image2, size)
        sub_image1 = cv2.split(image1)
        sub_image2 = cv2.split(image2)
        sub_data = 0
        for im1, im2 in zip(sub_image1, sub_image2):
            sub_data += self.calculate(im1, im2)
        sub_data = sub_data / 3
        return sub_data

二、灰度图算法：利用灰度图的值、均值、方差计算图像的差异性

（1）MSE（Mean Squared Error）均方误差：针对单通道灰度图

对于两个m×n的单通道图像I和K，它们的均方误差可定义为：

缺点：当差值大于1时，会放大误差；而当差值小于1时，则会缩小误差，这是平方运算决定的。MSE对于较大的误差(>1)给予较大的惩罚，较小的误差(<1）给予较小的惩罚。也就是说，对离群点比较敏感，受其影响较大。

（2）SSIM（structural similarity）结构相似性：针对单通道灰度图

SSIM(structural similarity)，结构相似性，是一种衡量两幅图像相似度的指标。

SSIM公式基于样本x和y之间的三个比较衡量：亮度 (luminance)、对比度 (contrast) 和结构 (structure)。

​

𝝁𝒙为均值， 𝝈𝒙 为方差， 𝝈𝒙𝒚 表示协方差。

​

常数𝑪𝟏， 𝑪𝟐， 𝑪𝟑是为了避免当分母为 0 时造成的不稳定问题。

​

在实际应用中，可以利用滑动窗将图像分块，令分块总数为N，考虑到窗口形状对分块的影响，采用高斯加权计算每一窗口的均值、方差以及协方差，然后计算对应块的结构相似度SSIM，最后将平均值作为两图像的结构相似性度量，即平均结构相似性SSIM。

def contrast_image(imageA, imageB):
        """
        对比两张图片的相似度，相似度等于1 完美匹配
        :param imageA:
        :param imageB:
        :return:
        """
        imageA = cv2.imread(imageA)
        imageB = cv2.imread(imageB)
        grayA = cv2.cvtColor(imageA, cv2.COLOR_BGR2GRAY)
        grayB = cv2.cvtColor(imageB, cv2.COLOR_BGR2GRAY)
        # 计算两个灰度图像之间的结构相似度指数,相似度等于1完美匹配
        (score, diff) = structural_similarity(grayA, grayB, full=True)
        diff = (diff * 255).astype("uint8")
        print("SSIM:{}".format(score))
        return score, diff

skimage.metrics包下的SSIM算法

def structural_similarity(*, im1, im2,
                         win_size=None, gradient=False, data_range=None,
                         multichannel=False, gaussian_weights=False,
                         full=False, **kwargs)

 返回值：
mssim—平均结构相似度
grad—结构相似性梯度 (gradient=True)
S—结构相似性图像(full=True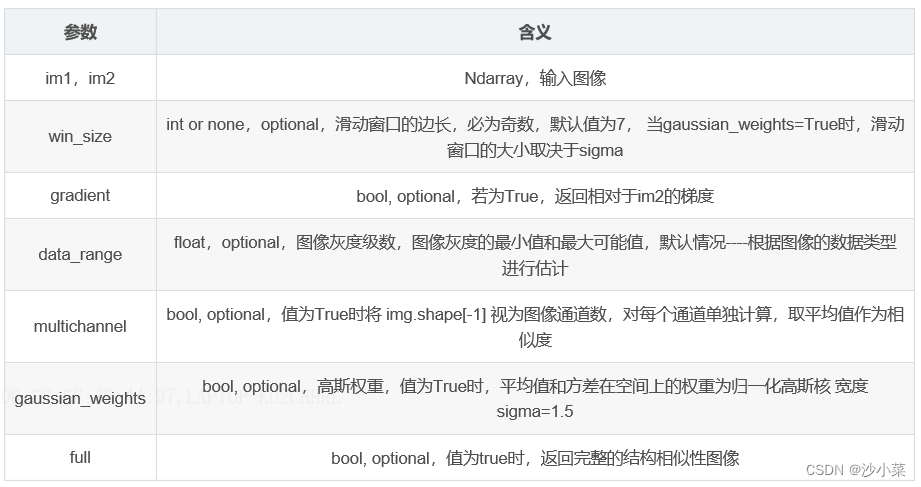

（3）图片相似度算法（对像素求方差并比对）的学习

步骤：

1)缩放图片

       将需要处理的图片所放到指定尺寸，缩放后图片大小由图片的信息量和复杂度决定。譬如，一些简单的图标之类图像包含的信息量少，复杂度低，可以缩放小一点。风景等复杂场景信息量大，复杂度高就不能缩放太小，容易丢失重要信息。根据自己需求，弹性的缩放。在效率和准确度之间维持平衡。

2)灰度处理

　　通常对比图像相似度和颜色关系不是很大，所以处理为灰度图，减少后期计算的复杂度。如果有特殊需求则保留图像色彩。

3)计算平均值

　　此处开始，与传统的哈希算法不同：分别依次计算图像每行像素点的平均值，记录每行像素点的平均值。每一个平均值对应着一行的特征。

4)计算方差

　　对得到的所有平均值进行计算方差，得到的方差就是图像的特征值。方差可以很好的反应每行像素特征的波动，既记录了图片的主要信息。

5)比较方差

        经过上面的计算之后，每张图都会生成一个特征值（方差）。到此，比较图像相似度就是比较图像生成方差的接近成程度。
　　一组数据方差的大小可以判断稳定性，多组数据方差的接近程度可以反应数据波动的接近程度。我们不关注方差的大小，只关注两个方差的差值的大小。方差差值越小图像越相似！

（4）PSNR

def PSNR(img1, img2):
 
    mse = np.mean((img1/255. - img2/255.) ** 2)
 
    if mse == 0:
 
        return 100
 
    PIXEL_MAX = 1
 
    return 20 * math.log10(PIXEL_MAX / math.sqrt(mse))

三、哈希算法

计算图片的哈希表示后，利用汉明距离计算两张图片的差异

哈希相似度

实现图片相似度比较的hash算法有三种：均值哈希算法（AHash），差值哈希算法（DHash），感知哈希算法 （PHash）。（图片转成哈希表示后，用汉明距离计算两个图片的差距）

• aHash：平均值哈希。速度比较快，但是常常不太精确。
• pHash：感知哈希。精确度比较高，但是速度方面较差一些。
• dHash：差异值哈希。精确度较高，且速度也非常快。

（1）均值哈希算法（AHash）

具体步骤：

1. 缩小尺寸：将图片缩小到8x8的尺寸，总共64个像素。这一步的作用是去除图片的细节，只保留结构、明暗等基本信息，摒弃不同尺寸、比例带来的图片差异。
2. 简化色彩：将缩小后的图片，转为64级灰度。也就是说，所有像素点总共只有64种颜色。
3. 计算平均值：计算所有64个像素的灰度平均值
4. 比较像素的灰度：将每个像素的灰度，与平均值进行比较。大于或等于平均值，记为1；小于平均值，记为0。
5. 计算哈希值：将上一步的比较结果，组合在一起，就构成了一个64位的整数，这就是这张图片的指纹。组合的次序并不重要，只要保证所有图片都采用同样次序就行了。

分析： 均值哈希算法计算速度快，不受图片尺寸大小的影响，但是缺点就是对均值敏感，例如对图像进行伽马校正或直方图均衡就会影响均值，从而影响最终的hash值。

def aHash(img):
        # 平均值哈希算法
        # 缩放为8*8
        img = cv2.resize(img, (8, 8))
        # 转换为灰度图
        gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
        # s为像素和初值为0，hash为hash值初值为''
        s = 0
        hash= ''
        # 遍历累加求像素和
        for i in range(8):
            for j in range(8):
                s = s + gray[i, j]
        # 求平均灰度
        avg = s / 64
        # 灰度大于平均值为1相反为0生成图片的hash值
        for i in range(8):
            for j in range(8):
                if gray[i, j] > avg:
                    hash_str = hash + '1'
                else:
                    hash_str = hash + '0'
        return hash_str

（2）感知哈希算法 （PHash）

感知哈希算法是一个比均值哈希算法更为健壮的一种算法，与均值哈希算法的区别在于感知哈希算法是通过DCT（离散余弦变换）来获取图片的低频信息。

具体步骤：

1. 缩小尺寸：pHash以小图片开始，但图片大于8x8，32x32是最好的。这样做的目的是简化了DCT的计算，而不是减小频率。
2. 简化色彩：将图片转化成灰度图像，进一步简化计算量。
3. 计算DCT：计算图片的DCT变换，得到32x32的DCT系数矩阵。
4. 缩小DCT：虽然DCT的结果是32x32大小的矩阵，但我们只要保留左上角的8x8的矩阵，这部分呈现了图片中的最低频率。
5. 计算平均值：如同均值哈希一样，计算DCT的均值。
6. 计算hash值：这是最主要的一步，根据8x8的DCT矩阵，设置0或1的64位的hash值，大于等于DCT均值的设为”1”，小于DCT均值的设为“0”。组合在一起，就构成了一个64位的整数，这就是这张图片的指纹。

分析： 结果并不能告诉我们真实性的低频率，只能粗略地告诉我们相对于平均值频率的相对比例。只要图片的整体结构保持不变，hash结果值就不变。能够避免伽马校正或颜色直方图被调整带来的影响。对于变形程度在25%以内的图片也能精准识别。

def pHash(img):
        # 感知哈希算法
        # 缩放32*32
        img = cv2.resize(img, (32, 32))  # , interpolation=cv2.INTER_CUBIC
 
        # 转换为灰度图
        gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
        # 将灰度图转为浮点型，再进行dct变换，cv2.dct()是离弦余弦变换
        dct = cv2.dct(np.float32(gray))
        # opencv实现的掩码操作
        dct_roi = dct[0:8, 0:8]
 
        hash = []
        avreage = np.mean(dct_roi)
        for i in range(dct_roi.shape[0]):
            for j in range(dct_roi.shape[1]):
                if dct_roi[i, j] > avreage:
                    hash.append(1)
                else:
                    hash.append(0)
        return hash

（3）差值哈希算法（DHash）

比pHash，dHash的速度要快的多，相比aHash，dHash在效率几乎相同的情况下的效果要更好，它是基于渐变实现的。

主要步骤：

1. 缩小尺寸：收缩到8x9（高x宽）的大小，一遍它有72的像素点
2. 转化为灰度图：把缩放后的图片转化为256阶的灰度图。
3. 计算差异值：dHash算法工作在相邻像素之间，这样每行9个像素之间产生了8个不同的差异，一共8行，则产生了64个差异值
4. 获得指纹：如果左边的像素比右边的更亮，则记录为1，否则为0

def dHash(img):
        # 差值哈希算法
        # 缩放8*8
        img = cv2.resize(img, (9, 8))
        # 转换灰度图
        gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
        hash = ''
        # 每行前一个像素大于后一个像素为1，相反为0，生成哈希
        for i in range(8):
            for j in range(8):
                if gray[i, j] > gray[i, j + 1]:
                    hash_str = hash + '1'
                else:
                    hash_str = hash + '0'
        return hash_str

汉明距离计算两个图像的哈希差值

def cmpHash(hash1,hash2):
    n=0
    #hash长度不同则返回-1代表传参出错
    if len(hash1)!=len(hash2):
         return -1
    #遍历判断
    for i in range(len(hash1)):
         #不相等则n计数+1，n最终为相似度
         if hash1[i]!=hash2[i]:
                n=n+1
    return n

MD5

粗暴的md5比较 返回是否完全相同

def md5_similarity(img1_path, img2_path):
    file1 = open(img1_path, "rb")
    file2 = open(img2_path, "rb")
    md = hashlib.md5()
    md.update(file1.read())
    res1 = md.hexdigest()
    md = hashlib.md5()
    md.update(file2.read())
    res2 = md.hexdigest()
    return res1 == res2

余弦相似度

把图片表示成一个向量，两个向量夹角的余弦值作为衡量两个个体间差异的大小。

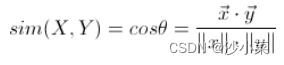
欧氏距离

衡量的是多维空间中各个点之间的绝对距离。

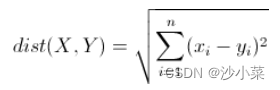
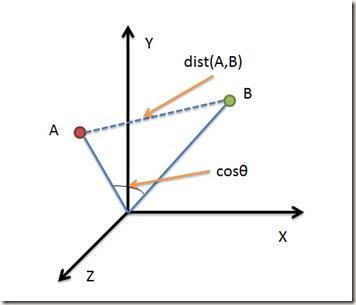
借助三维坐标系来看下欧氏距离和余弦距离的区别：

从上图可以看出，

欧氏距离衡量的是空间各点的绝对距离，跟各个点所在的位置坐标直接相关；

余弦距离衡量的是空间向量的夹角，更加体现在方向上的差异，而不是位置。

如果保持A点位置不变，B点朝原方向远离坐标轴原点，那么这个时候余弦距离 cos是保持不变的（因为夹角没有发生变化），而A、B两点的距离显然在发生改变，这就是欧氏距离和余弦距离之间的不同之处。

欧氏距离和余弦距离各自有不同的计算方式和衡量特征，因此它们适用于不同的数据分析模型：

欧氏距离能够体现个体数值特征的绝对差异，所以更多的用于需要从维度的数值大小中体现差异的分析，如使用用户行为指标分析用户价值的相似度或差异。

余弦距离更多的是从方向上区分差异，而对绝对的数值不敏感，更多的用于使用用户对内容评分来区分兴趣的相似度和差异，同时修正了用户间可能存在的度量标准不统一的问题（因为余弦距离对绝对数值不敏感）。

【精选】图像相似度匹配——距离大全_pairwise_distances图像距离-CSDN博客
​​​​​​​